Курсовая работа по прикладной механике и деталям машин. приклад курсач. Курсовой проект по прикладной механике является самостоятельной работой студента, завершающей изучение этой дисциплины. В процессе разработки проекта применены
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
3 Кинематический анализ механизма3.1 Построение плана положений механизмаКинематический анализ механизма – это аналитический или графический процесс расчета, в результате которого определяется положение звеньев, скорости и ускорения механизма. План положений механизма (ППМ) это графическое отображение механизма в выбранном масштабе при заданном положении ведущего (начального) звена. ППМ строится графическим методом (методом засечек). Под масштабом 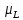 будем понимать отношение истинной длины звена (м) к отрезку в мм, изображающему это звено. Нужно определить масштаб плана положений механизма, который наиболее рационально рассчитывать с учетом Самого большого звена (коромысла 3) и возможности разместить план на ¼ листа формата А1. При заданных размерах звеньев план положений механизма изображаем в масштабе будем понимать отношение истинной длины звена (м) к отрезку в мм, изображающему это звено. Нужно определить масштаб плана положений механизма, который наиболее рационально рассчитывать с учетом Самого большого звена (коромысла 3) и возможности разместить план на ¼ листа формата А1. При заданных размерах звеньев план положений механизма изображаем в масштабе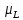 = = = 0,0147 = 0,0147 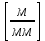 , (3.1) , (3.1)где 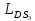 - длина звена CD; - длина звена CD; 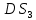 - отрезок в миллиметрах, изображающий звено на ППМ. - отрезок в миллиметрах, изображающий звено на ППМ.Для определения численного значения отрезков, изображающих звенья механизма на ППМ необходимо их истинный размер разделить на выбранный масштаб длины. Находим отрезки изображающие звенья механизма на чертеже и результаты сводим в таблицу 1. Т а б л и ц а 1 – Размеры звеньев механизма на ППМ
По полученным значениям длин звеньев при заданном угле поворота кривошипа 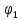 =235˚ нужно построить план положения рычажного механизма в основном положении. =235˚ нужно построить план положения рычажного механизма в основном положении.Затем надо изобразить механизм в крайних положениях, т.е. таких, когда ведомое звено 5 может двигаться только в одном направлении. Одно крайнее (верхнее) положение получается, если из точки О сделать засечку на траектории движения точки В коромысла 3 радиусом (AB-OA) = 88,435 мм. Другое крайнее (нижнее) положение получается засечкой радиусом (AB+OA) = 156,463 мм. Получаем верхнюю D1 (ВМТ) и нижнюю D2 (НМТ) мертвые точки ведомого звена. Расстояние между ними называется ходом поршня и определяется по зависимости 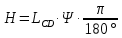 , (3.2) , (3.2) где 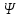 – угол между OD1 и OD2. – угол между OD1 и OD2.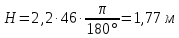 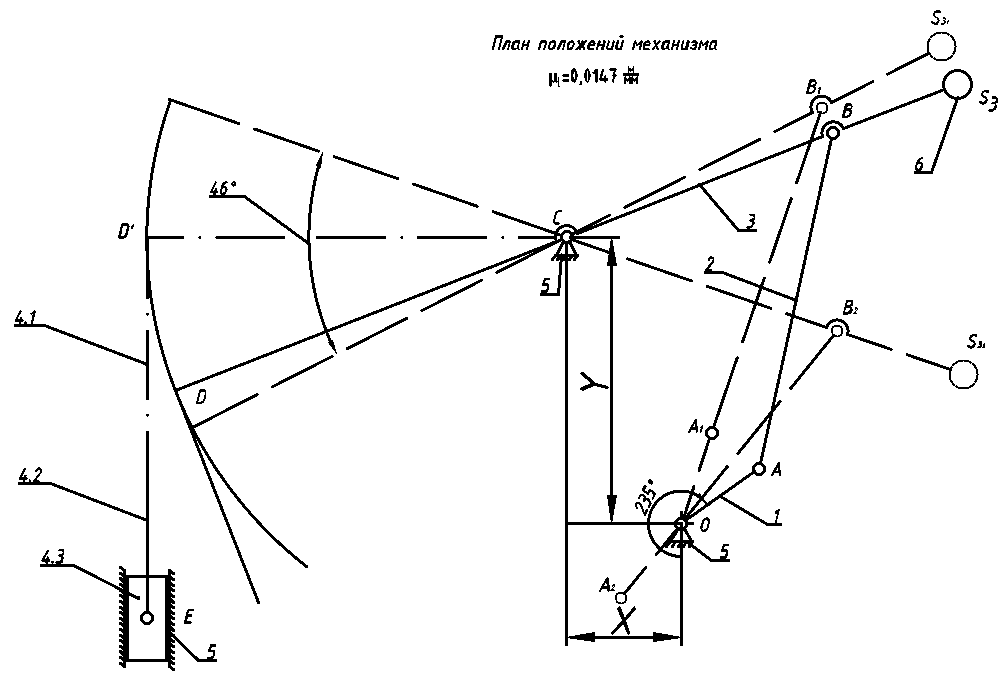 Рисунок 3 – План положений механизма 3.2 Определение скоростей точек механизма и угловых скоростей звеньев механизма. План скоростей механизмаДля определения скоростей точек механизма воспользуемся графоаналитическим методом расчета с помощью построения плана скоростей механизма. План скоростей механизма (ПСМ) – графическое векторное масштабное изображение скоростей точек механизма для заданного положения механизма. Для построения ПСМ необходимо аналитически определить линейную скорость точки А кривошипа, которая определяется по следующей зависимости:  , (3.3) , (3.3)где 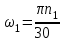 – угловая скорость кривошипа, с-1; – угловая скорость кривошипа, с-1; - длина кривошипа, м. - длина кривошипа, м.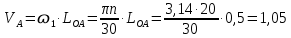 м/c м/cСкорости остальных точек механизма находим графически, путем построения плана скоростей. Для этого определим масштаб плана скоростей механизма:  , (3.4) , (3.4)где  - отрезок на ПСМ в мм, изображающий скорость - отрезок на ПСМ в мм, изображающий скорость 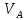 . .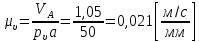 . .Скорость точки В определяем из следующего векторного уравнения: 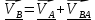 . (3.5) . (3.5)Анализируем векторное уравнение (3.5). Скорость точки В ( 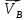 ) известна по направлению, так как точка В в своем абсолютном движении совершает вращательное движение вокруг точки С, то ее скорость будет перпендикулярна участку ВС звена 3 ( ) известна по направлению, так как точка В в своем абсолютном движении совершает вращательное движение вокруг точки С, то ее скорость будет перпендикулярна участку ВС звена 3 (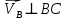 ). ). Скорость точки А ( 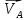 ) известна и по величине и по направлению. Так как точка А совершает вращательное движение вокруг неподвижной точки О, то ее линейная (окружная) скорость направлена в сторону угловой скорости звена 1 перпендикулярно радиусу вращения, т.е. звену ОА ( ) известна и по величине и по направлению. Так как точка А совершает вращательное движение вокруг неподвижной точки О, то ее линейная (окружная) скорость направлена в сторону угловой скорости звена 1 перпендикулярно радиусу вращения, т.е. звену ОА (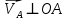 ). ).Скорость точки В относительно точки А ( 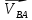 ) известна по направлению, так как точка В в своем относительном движении совершает вращательное движение вокруг точки А, то ее скорость будет перпендикулярна звену АВ ( ) известна по направлению, так как точка В в своем относительном движении совершает вращательное движение вокруг точки А, то ее скорость будет перпендикулярна звену АВ (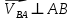 ). ).Скорости известные только по направлению подчеркиваем одной чертой, а известные по направлению и величине – двумя. Анализ векторного уравнения (3.5) показал, что неизвестны только две скорости по величине, и такое уравнение решается графически. Выбираем на плоскости произвольную точку 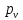 - полюс плана скоростей и из нее в направлении скорости - полюс плана скоростей и из нее в направлении скорости 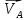 откладываем отрезок равный откладываем отрезок равный  . Через конец полученного отрезка проводим линию действия . Через конец полученного отрезка проводим линию действия 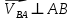 , а через полюс построения линию действия , а через полюс построения линию действия 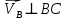 . Точка пересечения линий действия . Точка пересечения линий действия 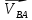 и и 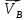 дает решение векторного уравнения 3.5. Измерив соответствующие отрезки на ПСМ определим скорости дает решение векторного уравнения 3.5. Измерив соответствующие отрезки на ПСМ определим скорости 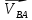 и и 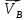 . .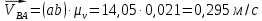 . .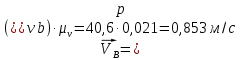 . .Определяем угловые скорости звеньев 2 и 3 по зависимости: 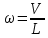 , с-1. (3.6) , с-1. (3.6)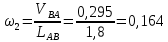 с-1. с-1. с-1. с-1.Учитывая, что все точки звена 3 имеют одинаковую угловую скорость, определим линейные скорости точек S3 и D: 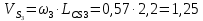 м/с. м/с.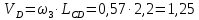 м/с. м/с.Скорость точки D ( 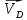 ) известна и по величине и по направлению. Так как точка D совершает вращательное движение вокруг неподвижной точки C, то её линейная (окружная) скорость направлена в сторону угловой скорости звена 3 перпендикулярно радиусу вращения, т.е. отрезку CD звена 3 ( ) известна и по величине и по направлению. Так как точка D совершает вращательное движение вокруг неподвижной точки C, то её линейная (окружная) скорость направлена в сторону угловой скорости звена 3 перпендикулярно радиусу вращения, т.е. отрезку CD звена 3 (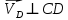 ). ).Скорость точки E ( 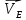 ) известна по направлению. Так как точка E в своём абсолютном движении совершает возвратно–поступательное движение вдоль направляющей , то её скорость будет параллельна направляющей ) известна по направлению. Так как точка E в своём абсолютном движении совершает возвратно–поступательное движение вдоль направляющей , то её скорость будет параллельна направляющей 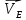 || ). || ).Скорость точки E ( 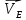 ) будет равна по модулю скорости точки D ( ) будет равна по модулю скорости точки D (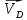 ), так как конец троса закреплен на звене 3. ), так как конец троса закреплен на звене 3. Из полюса плана скоростей проводим линию действия 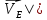 , а через конец вектора , а через конец вектора 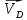 проводим дугу радиусом, равным отрезку pvd на ПСМ до пересечения с линией, параллельной направляющей . Точка пересечения линий действия проводим дугу радиусом, равным отрезку pvd на ПСМ до пересечения с линией, параллельной направляющей . Точка пересечения линий действия 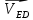 и дуги даёт отрезок (pvd), изображающий скорость и дуги даёт отрезок (pvd), изображающий скорость 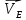 . .Результаты вычислений и построений сводим в табл.2. Т а б л и ц а 2 – Сводная таблица скоростей точек и звеньев механизма
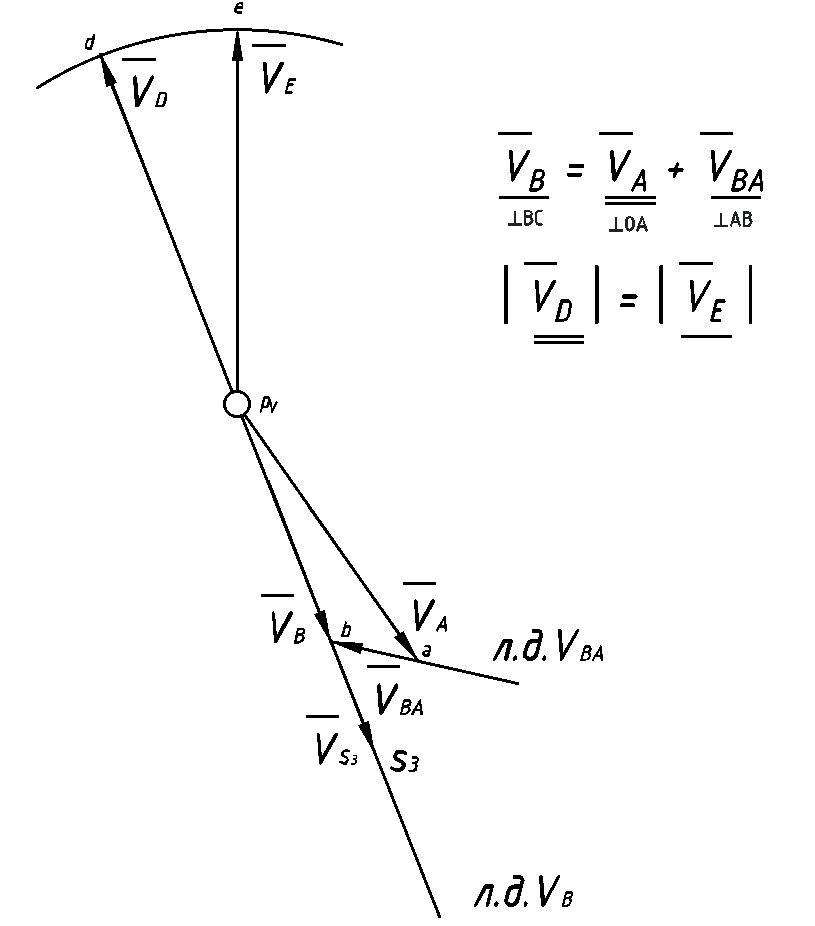 Рисунок 4 - План скоростей механизма |