Курсовая работа по прикладной механике и деталям машин. приклад курсач. Курсовой проект по прикладной механике является самостоятельной работой студента, завершающей изучение этой дисциплины. В процессе разработки проекта применены
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
4 Силовое исследование рычажного механизма4.1 Силовое исследование структурного элемента (звено 4)Задачей силового расчета механизма является определение реакций во всех кинематических парах и величины уравновешивающего момента (или уравновешивающей силы) на входном звене. Силовой расчет начинается с определения всех внешних сил (рабочих усилий, сил инерции, веса и т.п.), действующих на звенья механизма. Силовой расчет начинается с последней присоединенной группы Ассура и заканчивается расчетом входного звена механизма. Силовой расчет производится с учетом ускоренного движения методом кинетостатики. Метод основан на применении принципа Даламбера, при котором после добавления к внешним силам сил инерции механизм условно считается неподвижным и для определения неизвестных сил применяют уравнения статики. Силами трения при расчете ввиду их незначительности пренебрегаем. Механизм глубинного насоса включает две группы Ассура и начальное звено (кривошип ОА). Силовой расчет механизма выполняем для заданного положения механизма (для этого положения построен и план ускорений). На рисунке 6 представлена схема сил действующих на структурный элемент (звено 4). В соответствии с планом скоростей (рисунок 5) звено 4 движется вверх и поднимает жидкость. Сила инерции звена 4 направлена противоположно ускорению центра масс звена ( 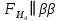 ) и определяется по зависимости: ) и определяется по зависимости: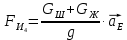 , Н, (4.1) , Н, (4.1)где 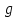 - ускорение свободного падения, - ускорение свободного падения, 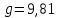 м/с2. м/с2. кН. кН.Реакция со стороны отброшенного звена 3 на звено 4 направлена вдоль звена 4, поскольку массой четвертого звена по заданию пренебрегаем ( 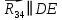 ). ).Согласно принципу Даламбера можно записать следующее векторное уравнение равновесия для звена 4:  (4.2) (4.2)Силы известные только по направлению подчеркиваем одной чертой, а известные по направлению и величине – двумя. Анализ векторного уравнения (4.2) и рисунка 6 показывает, что силы направлены по одной оси и в уравнении одна неизвестная, следовательно, уравнение (4.2) можно записать в алгебраическом виде: 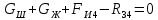 (4.3) (4.3)Откуда получаем неизвестную величину реакции R34: 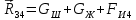 ; (4.4) ; (4.4)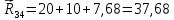 кН. кН.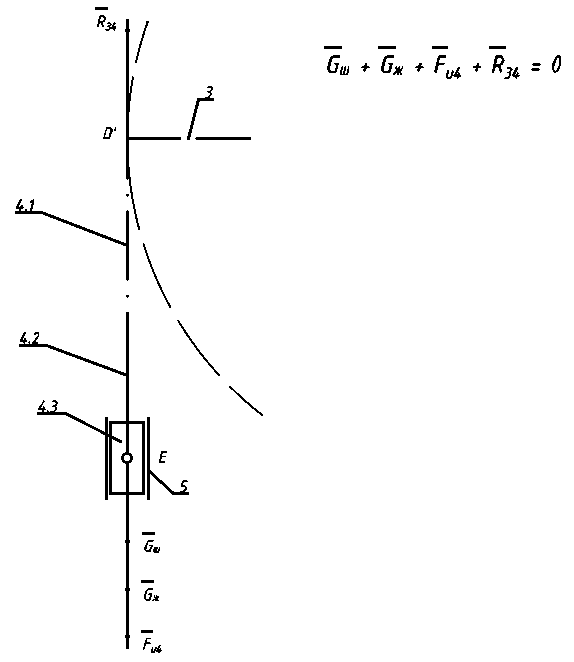 Рисунок 6 – Схема сил, действующих на структурный элемент 4.2 Силовое исследование диады (звенья 2, 3)Для определения усилий действующих на звенья диады 2 и 3 составим схему сил. К звеньям диады прикладываем силы тяжести, реакции отброшенных связей, силы инерции звеньев и согласно принципу Даламбера записываем векторное уравнение равновесия:  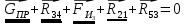 , (4.5) , (4.5)где 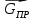 - сила тяжести противовеса, Н; - сила тяжести противовеса, Н;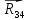 - реакция со стороны отброшенного звена 4, - реакция со стороны отброшенного звена 4,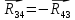 ; ; - сила инерции центра масс звена 3; - сила инерции центра масс звена 3;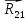 - реакция со стороны отброшенного звена 1; - реакция со стороны отброшенного звена 1;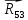 - реакция со стороны отброшенного звена 5. - реакция со стороны отброшенного звена 5.Сила инерции центра масс звена 3 направлена противоположно ускорению точки F ( 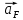 ) и определяется по формуле: ) и определяется по формуле: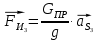 . (4.6) . (4.6)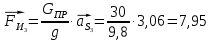 кН. кН.Анализируя векторное уравнение (4.5) видим, что первые три слагаемых известны и по направлению и по величине, реакция  известна только по направлению ( известна только по направлению ( ), а реакция ), а реакция 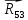 не известна ни по направлению, ни по величине. Таким образом, в векторном уравнении (4.5) три неизвестных величины и графически такое уравнение не решается. Поэтому составляем дополнительное уравнение равновесия статики для определения величины реакции не известна ни по направлению, ни по величине. Таким образом, в векторном уравнении (4.5) три неизвестных величины и графически такое уравнение не решается. Поэтому составляем дополнительное уравнение равновесия статики для определения величины реакции  , сумму моментов всех сил , сумму моментов всех сил  относительно точки С. относительно точки С.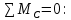 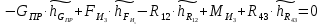 , (4.7) , (4.7)где:  , кН м . , кН м .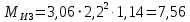 кН кН м. м.откуда находим  : :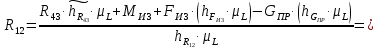 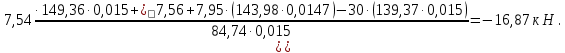 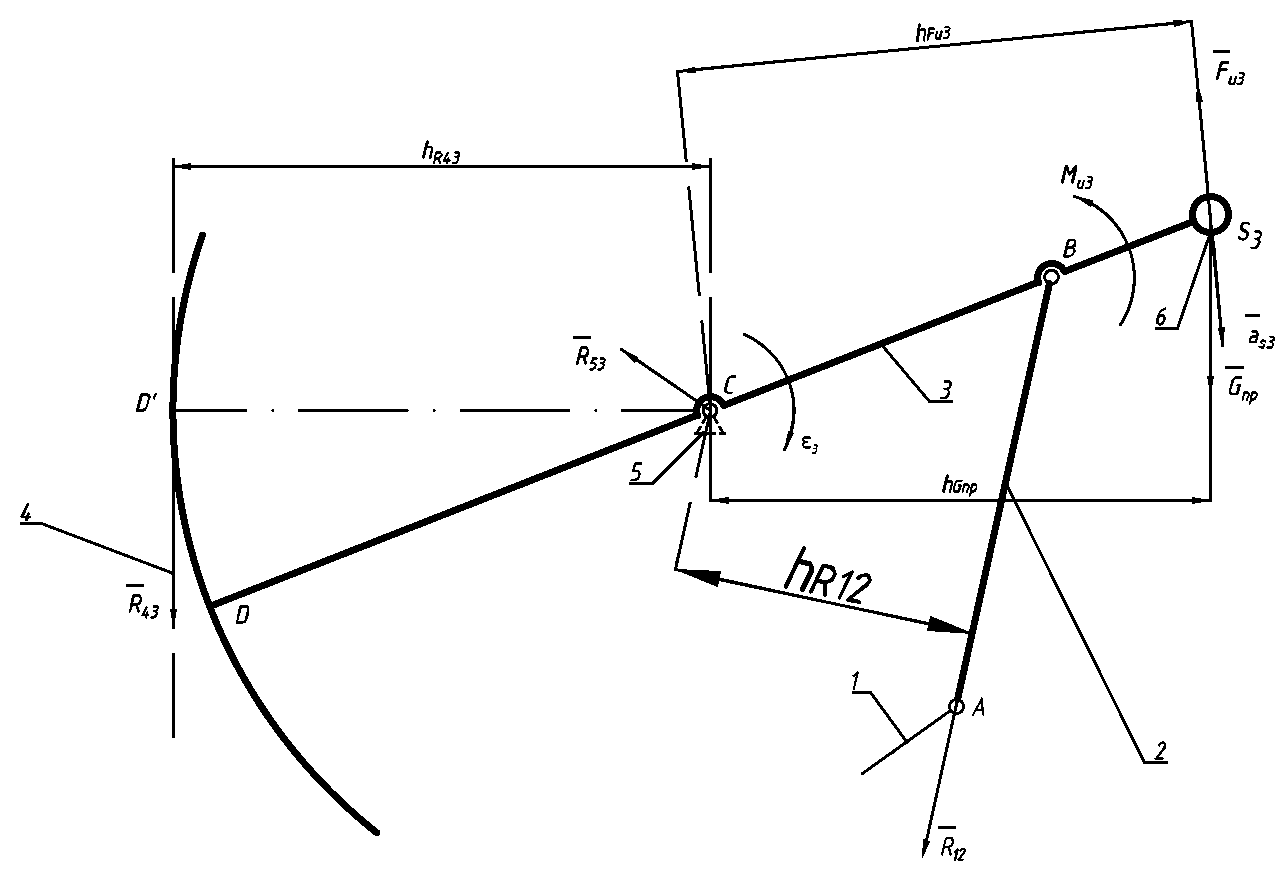 Рисунок 7 – Схема сил, действующих на звенья 2 и 3 После этого в уравнении (4.5) остается только две неизвестных и такое векторное уравнение можно решить графически. 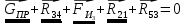 . .Определим масштаб плана сил диады из следующего выражения: 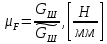 , (4.8) , (4.8)где 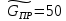 мм - отрезок на плане сил, изображающий мм - отрезок на плане сил, изображающий 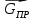 . .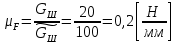 . .Остальные известные усилия переводим в соответствующие отрезки на плане сил. План сил диады (звенья 2 и 3) в выбранном масштабе приведен на листе 2 графической части курсового проекта. В результате получены длины отрезков изображающих неизвестные реакции в кинематических парах диады. Измерив получившиеся отрезки и умножив их на масштаб построения, получаем величины реакций в кинематических парах: 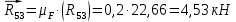 ; ;Реакции в кинематической паре В равны между собой по абсолютной величине и равны модулю реакции 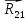 . .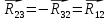 (4.9) (4.9) Рисунок 8 – План сил диады (звенья 2,3) |
