Курсовой проект Привод общего назначения

• Название: Курсовой проект Привод общего назначения
• Дата: 06.09.2022
• Размер: 5.7 Mb.
• Имя файла: kursovoi_proekt (17).docx
• Тип: Курсовой проект; #663930
• страница: 7 из 22

3.3. Определение коэффициента нагрузки

Коэффициент нагрузки для червячных передач определяется по формуле:

,

(3.13)

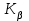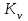где – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении.

Поскольку зубья червячного колеса обладают способностью прирабатываться, при постоянной нагрузке (в соответствии с заданием на курсовое проектирование) происходит их полная приработка и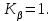

Коэффициент 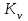зависит в основном от степени точности передачи и от скорости скольжения V_ск в зацеплении (см. табл. 3.3). По СТ СЭВ установлено 12 степеней точности для червячных передач. Для силовых передач предназначаются степени от 5 до 9-й в порядке убывания точности. Для редукторов общего назначения применяют в основном 7 и 8-ю степени точности.

При скоростях скольжения, для которых в таблице 3.3 значения 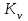не указаны, соответствующие точности изготовления передач не применяются. Таким образом, таблица 3.3 может быть также использована для назначения степени точности передачи.


Таблица 3.3

Коэффициент динамичности нагрузки К_v

Степень точности передачи	Скорость скольжения Vск, м/с
	до 1,5	от 1,5 до 3,0	от 3,0 до 7,5	от 7,5 до 12
6	–	–	1	1,1
7	1	1	1,1	1,2
8	1,15	1,25	1,4	–
9	1,25	–	–	–

3.4. Проектный расчет червячной передачи

Проектный расчет червячной передачи заключается в определении главного параметра передачи – межосевого расстояния а_w, характеризующего её габаритные размеры, массу и нагрузочную способность из условия контактной прочности. По величине а_w определяют (назначают) остальные геометрические параметры червячной передачи.

Для червячной передачи расчет из условия контактной прочности обеспечивает отсутствие не только выкрашивания, но и заедания, приводящего к задирам рабочих поверхностей зубьев червячного колеса.

Предварительное значение межосевого расстояния

Предварительное значение определяется по формуле:

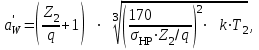(3.14)

где:

Z₂ – число зубьев червячного колеса;

q – коэффициент диаметра червяка;

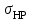– допускаемое контактное напряжение (см. п. 3.2);

Т₂ – момент сопротивления на валу червячного колеса;

k – коэффициент нагрузки (см. п. 3.3).

В формулу следует подставлять 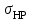в МПа, Т₂ – в Н∙мм, при этом 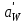будет получено в мм.

При определении предварительного значения 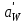следует задать из условия достаточной жесткости червяка при изгибе Z₂ / q = 4,0.

Если проектируемый червячный редуктор предназначен для серийного выпуска, то полученное по формуле значение 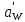округляется до ближайшего значения по ГОСТ 2144-66; 63; 80; 100; 125; (140); 160; (180); 200; (225); 250; (280); 315; (355) мм. Для нестандартных червячных передач это требование не является целым числом миллиметров (желательно из ряда нормальных линейных размеров).

Расчет числа зубьев червячного колеса

Расчет числа зубьев червячного колеса осуществляется по формуле:

.

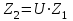(3.15)

Рекомендуемые значения Z₂ должны находиться в пределах .

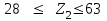При Z₂ < 28 получается слишком крупным модуль передачи, при Z₂ > 63 значительно снижается изгибная прочность зубьев червячного колеса.

Определяя Z₂, необходимо число заходов червяка Z₁ = 1; 2; 4 выбрать таким, чтобы при заданном передаточном числе U величина Z₂ находилась в заданных пределах.

Выбор осевого модуля передачи

При правильно выбранном значении Z₂ прочность зубьев червячного колеса по изгибу не является лимитирующим фактором, поэтому модуль передачи m выбирается из геометрических соображений по формуле:

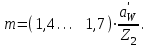(3.16)

Полученное по формуле значение m следует округлить до стандартного по ГОСТ 2144-76: 2; 2,5; (3); 3,15; (3,5); 4,0; 5,0; (6,0); 6,3; 7,0; 8,0; 10; 12; 12,5; 16 мм и т. д. В скобках указаны менее предпочтительные значения.

Определение коэффициента диаметра червяка

Коэффициент диаметра червяка рассчитывается по формуле:

.

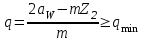(3.17)

Здесь 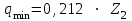выбирается из условия минимально допустимой жесткости червяка на изгиб.

Полученное по формуле значение q должно соответствовать указанному в ГОСТ 2144-76: (7,1); 8; (9); 10; (11,12); 12,5; (14).

Фактическое значение межосевого расстояния передачи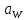

После определения основных характеристик передачи уточняется величина межосевого расстояния по формуле:

.

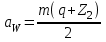(3.18)

Если величина межосевого расстояния не совпадает с принятым ранее стандартным значением 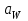, а по условиям проектирования необходимо вписаться в стандартное осевое расстояние, выполняется коррекция передачи путем смещения инструмента.

В учебном проектировании к коррекции червячных передач обычно не прибегают, используя для корректирования приведенные в таблице 3.4 сочетания стандартных (по ГОСТ 2144-76) параметров червячных редукторов, при которых стандартные межосевое расстояние 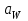получается без применения коррекции.
Таблица 3.4

Сочетания параметров червячных передач, обеспечивающие получение

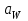
по ГОСТ 2144-76 без применения коррекции

U1	8	10	12,5	16	20	25	31,5	40	50
Z1	4			2			1
Z2	32	40	50	32	40	50	32	40	50
q	8	10	12,5	8	10	12,5	8	10	12,5

Определение геометрических параметров передачи

Геометрические параметры червяка изображены на рис 3.1.



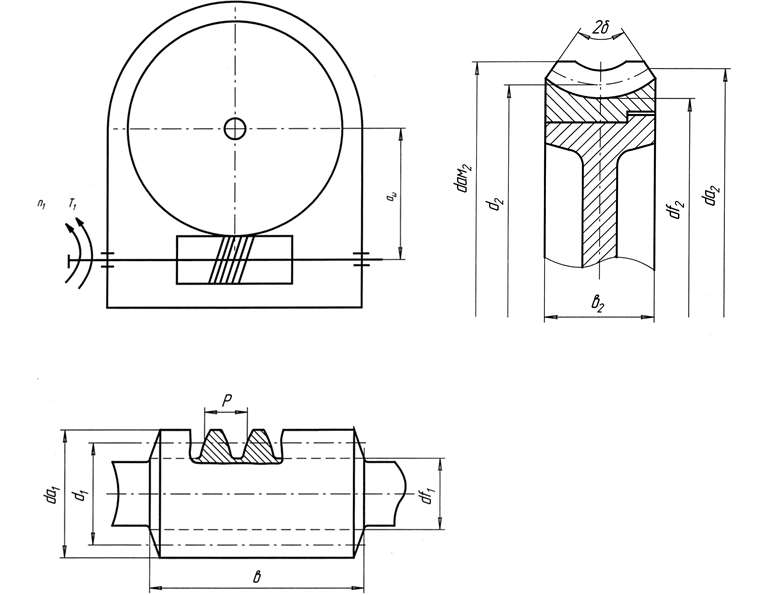
Рис. 3.1. Червячная передача
Делительный диаметр червяка рассчитывается по формуле:

.

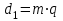(3.19)

Диаметр вершин витков червяка – по формуле:

.

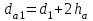(3.20)

Расчет диаметра впадин червяка осуществляется с помощью формулы:

.

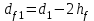(3.21)

Высота головки h_a и ножки h_f витков определяются по формулам ниже:

; ,

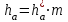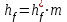(3.22)

где коэффициент высоты головки 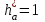, коэффициент высоты ножки 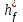для архимедовых и конволютных червяков равен 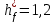, а для эвольвентных .

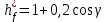Угол подъемов витков червяка рассчитывается по формуле:

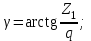(3.23)

длина нарезанной части червяка:

,

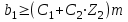(3.24)

где при Z₁ = 1 или 2 С₁ = 11, С₂ = 0,06; при Z₁ = 4 С₁ = 12,5, С₂ = 0,09.

Для шлифуемых червяков во избежание искажения рабочей части при входе и выходе шлифовального круга 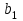увеличивают приблизительно на 3m.
Геометрические параметры червячного колеса

Делительный диаметр червячного колеса определяется по формуле:

.

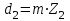(3.25)

Диаметр вершин зубьев червячного колеса – по формуле:

.

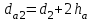(3.26)

Диаметр впадин червячного колеса:

.

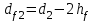(3.27)

Наибольший диаметр червячного колеса:

.

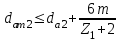(3.28)

Ширина венца червячного колеса:

при Z1 = 1 или 2 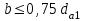; при Z1 = 4 .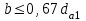

(3.29)

Условный угол обхвата рассчитывается по формуле:

.

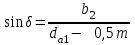(3.30)

Определение действительной скорости скольжения в червячном зацеплении

При известных геометрических параметрах передачи:

,

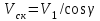(3.31)

где V₁ составляет:

;

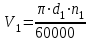(3.32)

угол подъема витков червяка рассчитывается по формуле:

.

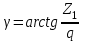(3.33)

Если действительное значение V_ск окажется больше, чем принятое в начале расчета (формула 3.1), то для тех передач, где допускаемые контактные напряжения определялись в зависимости от V_ск (материалы 2-й и 3-й групп), требуется уточнение величины σ_НP, а также коэффициента нагрузки k' при новом значении σ_НP (см. п.п. 3.2 и 3.3).
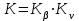