ТММ ВятГАТУ. Курсовой проект синтез и анализ плоских механизмов пояснительная записка вгсха. 012. 00. 69. 00 Пз
 Скачать 217.13 Kb. Скачать 217.13 Kb.
|
 Министерство сельского хозяйства Российской Федерации Министерство сельского хозяйства Российской ФедерацииФГБОУ ВО Вятская ГСХА Инженерный факультет Кафедра материаловедения, сопротивления материалов и деталей машин Курсовой проект СИНТЕЗ И АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ Пояснительная записка ВГСХА.012.00.69.00 ПЗ Направление подготовки: 35.03.06 Агроинженерия Профиль: Автомобили и технические системы в агробизнесеИсполнитель Чураков В.Э. Группа ИМбз-210 Руководитель Гребнев А.В. Киров 2020 СодержаниеПрофиль: Автомобили и технические системы в агробизнесе 1 1 Проектирование схемы, структурное и кинематическое исследование рычажного механизма 3 1.1 Структурный анализ механизма 4 1.2 Построение плана механизма 6 1.3 Построение планов скоростей механизма 6 1.4 Построение планов ускорений 8 2 Анализ зубчатого механизма 12 2.1 Определение передаточного отношения графическим методом 12 2.2 Определение передаточного отношения аналитическим методом 13 2.3 Проверка выполнения условий соосности, соседства и сборки планетарного механизма 13 3 Расчет маховика 15 Литература 19 Приложение А 20 1 Проектирование схемы, структурное и кинематическое исследование рычажного механизма Исходные данные: 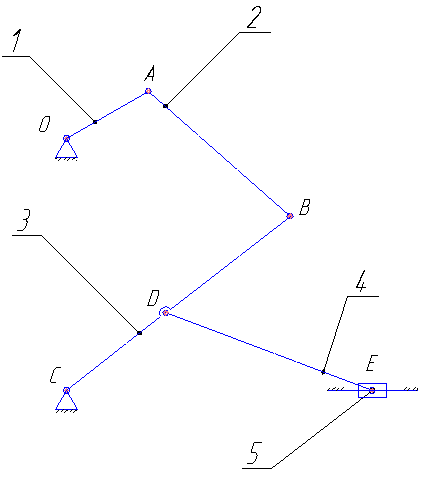    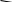 lOA=0,15м; lAB=0,35м; lСD=0,3м; lBC=0,4м; lDE=0,35м; xC=0м; yС=-0,3м; yE =-0,35 м; 1=10 с-1, φ0=80, Δφ=45, направление вращения - против часовой Требуется выполнить: провести структурный анализ механизма; построить два плана механизма; для каждого положения плана механизма построить план скоростей и план ускорений; вычислить линейные скорости и ускорения звеньев механизма. Результаты вычислений свести в таблицы; на планах механизма нанести направления угловых скоростей и ускорений соответствующих звеньев. 1.1 Структурный анализ механизма Определяем степень подвижности. Так как механизм плоский, то применяем формулу П.Л. Чебышева W = 3n – 2P5 – P4, где n – число подвижных звеньев; Р4, Р5 – число кинематических пар соответственно четвертого и пятого классов. n = 5; P5: O, A, B, D, C, Е45, Е56. P4 – нет. W = 3·5 – 2·7 – 0 = 1. Это значит, что данная кинематическая цепь является механизмом, в котором достаточно иметь одно ведущее звено. Для определения класса механизма разбиваем его на структурные группы, у каждой из которых определяем класс, порядок и вид. 3) 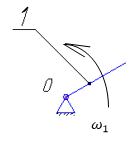 2) 2) 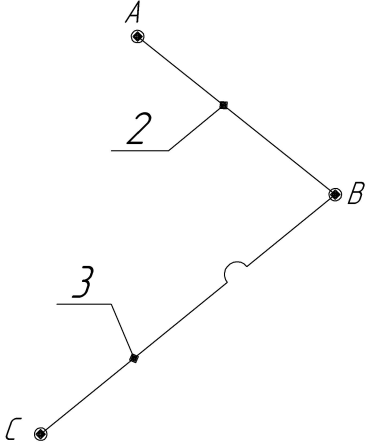 Механизм I класса II класс, 2 порядок, 1 вид. 1) 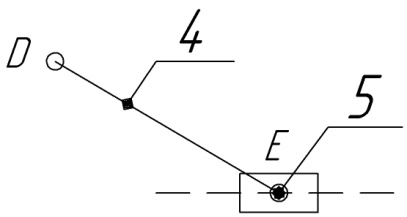 II класс, 2порядок, 2 вид. Имеем структурную группу ABС второго класса, второго порядка, первого вида, структурную группу DE второго класса, второго порядка, второго вида и механизм первого класса. Формула строения механизма имеет вид I (6,1) II (2,3) II (4,5). В целом механизм второго класса. Все механизмы второго класса исследуются методом планов. 1.2 Построение плана механизмаОпределяем масштаб для построения плана механизмаl = lOA/OA, где ОА – длина отрезка на плане механизма, изображающего кривошип. l = 0,15/30 = 0,005 м/мм. В принятом масштабе выражаем все остальные геометрические параметры и звенья механизма. АВ = lАB/l = 0,35/0,005 = 70 мм, XC = 0 мм, BC = lBC/l = 0,4/0,005 = 80 мм, YC = -60 мм, CD = lCD/l = 0,3/0,005 = 60 мм, YE = -70 мм DE = lDE/l = 0,35/0,005 = 70 мм, 1.3 Построение планов скоростей механизмаПостроение начинаем с определения линейной скорости точки А, принадлежащей ведущему звену ОА. VA = 1·lOA =10 ·0,15 = 1,5 м/с. Направление скорости точки А определится из векторного уравнения 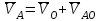 , ,где 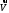 AO – вектор относительной скорости точки A относительно точки O, направлен перпендикулярно АO; AO – вектор относительной скорости точки A относительно точки O, направлен перпендикулярно АO;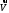 O - вектор абсолютной скорости точки O, скорость равна 0. O - вектор абсолютной скорости точки O, скорость равна 0.Из произвольно выбранной точки, называемой полюсом плана скоростей, проводим вектор Рa, перпендикулярный звену ОА, направленный в сторону угловой скорости 1. Длина отрезка принимается из условия получения «удобного» масштаба V. V=VA/PA=1,5 / 150 = 0,01(м/с)/мм. Скорость токи В определится из совместного решения двух векторных уравнений: 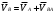 , , 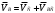 где 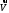 BA – вектор относительной скорости точки В относительно точки А, направлен перпендикулярно АВ; BA – вектор относительной скорости точки В относительно точки А, направлен перпендикулярно АВ;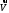 BС – вектор относительной скорости точки В относительно точки С, направлен перпендикулярно ВС; BС – вектор относительной скорости точки В относительно точки С, направлен перпендикулярно ВС;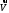 B - B - вектор абсолютной скорости точки В, принадлежащей звену 3 направлен перпендикулярно BC. вектор абсолютной скорости точки В, принадлежащей звену 3 направлен перпендикулярно BC.Из первого векторного уравнения следует, что для построения вектора 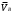 надо из конца известного вектора надо из конца известного вектора 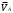 провести вектор провести вектор 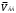 , который направлен перпендикулярно к звену АВ. Из второго векторного уравнения следует, что из точки С, которая совпадает с полюсом, нужно провести прямую, перпендикулярную СВ. Точка b найдется в пересечении этих двух прямых, а величина ее скорости из выражения , который направлен перпендикулярно к звену АВ. Из второго векторного уравнения следует, что из точки С, которая совпадает с полюсом, нужно провести прямую, перпендикулярную СВ. Точка b найдется в пересечении этих двух прямых, а величина ее скорости из выражения 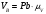 . .Скорость точки D определяем по теореме подобия из соотношения BC/CD=Pb/Pd. Pd лежит на отрезке Pb и имеет то же самое направление. 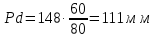 Для определения скорости точки Е, используем векторное уравнение 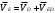 ; ;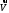 ED – вектор относительной скорости точки E относительно точки D, направлен перпендикулярно ED; ED – вектор относительной скорости точки E относительно точки D, направлен перпендикулярно ED;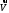 D - D - вектор абсолютной скорости точки D. вектор абсолютной скорости точки D.Через точку Р проводим линию, параллельную оси ОХ; из точки D проводим линию перпендикулярную ED. В пересечении находится точка e. Из плана скоростей определяем линейные скорости точек: VB=Pb·V=148·0,01=1,48м/с; VBA=ab·V=3·0,01=0,03м/с; VE=Pe·V=56·0,01=0,56м/с; VED=de·V =114·0,01=1,14м/с. и угловые скорости звеньев 2=VBA/lAB = 0,03/0,35=0,1с 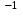 ; ;3=VB/lBC = 1,48/0,4=3,7с 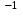 ; ;4=VED/lDE = 1,14/0,35=3,3с 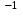 . .Полученные значения сводим в табл. 1. Таблица 1 - Значения линейных скоростей точек и угловых скоростей звеньев механизма
Направление угловой скорости звена определится, если вектор относительной скорости двух его точек мысленно перенести с плана скоростей на план механизма в точку, стоящую в индексе при скорости на первом месте. Например, для определения 2 прикладываем вектор VBA в точку В. Наносим направления угловых скоростей звеньев на план механизма. 1.4 Построение планов ускоренийУскорение точки А определяем из векторного уравнения 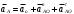 , ,где аО – абсолютное ускорение точки О, м/с², аО = 0, т.к. точка О неподвижна; аАОn – нормальное ускорение точки А относительно точки О, направлено вдоль звена к центру вращения, т.е. от точки А к точке О. аАОn = 1²·lOA = 10²·0,15 =15 м/с² где аАО - касательное ускорение точки А относительно точки О, аАО = 0, т.к. 1= const. Определяем масштаб плана ускорений А = аА/а = 15/150 = 0,1 (м/с²)/мм, где а=150мм – длина отрезка на плане ускорений, произвольно принятого нами длиной 150 мм из условия получения удобного масштаба. Из произвольно выбранной точки , называемой полюсом ускорений, проводим вектор а, длиной 150 мм параллельно звену ОА в направлении к точке О, как к центру вращения. Построение плана ускорений структурной группы (звенья 2, 3) II класса третьего вида проводим согласно системе уравнений 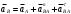 , ,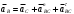 r, r,аВАn = 2²·lАВ = 0,1²·0,35 = 0 м/с². аВCn = 3²·lВc = 3,7²·0,4 = 6 м/с². Масштабная величина этого ускорения равна anВА= аВАn/А=0/0,1=0 мм;  nВС = аВCn/А=6/0,1=60мм; nВС = аВCn/А=6/0,1=60мм;Графическое решение векторных уравнений заключается в проведении из точек а и с на плане ускорений отрезков anВА и ,  nВС параллельных соответственно звеньям АВ и ВС и направленных к точкам А и С. nВС параллельных соответственно звеньям АВ и ВС и направленных к точкам А и С.Тангенциальные составляющие перпендикулярны к нормальным; в их пересечении определится точка В. Ускорение точки d на векторе 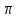 b определится по теореме подобия из соотношения CB/CD= b определится по теореме подобия из соотношения CB/CD=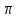 b/ b/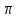 c. c.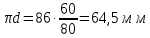 Ускорение точки Е, определится из векторных уравнений 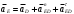 , ,где аD – абсолютное ускорение точкиD; аE – абсолютное ускорение точки Е; аEDn – нормальное ускорение точки E относительно точки D, направлено вдоль звена ED к точке D, как центру вращения аEDn = 4²·lCD = 3,3²·0,35=4м/с². Его масштабная величина dnED= аEDn /А=4/0,1=40мм; аED – касательное ускорение точки E относительно точки D, направлено перпендикулярно нормальному ускорению (его величина не известна). Для решения рассмотренной системы уравнений из точки D проводим вектор dnED, параллельный звену ED, в направлении точки e. Из конца вектора нормального ускорения dnED перпендикулярно ему проводим линию, а из точки проводим линию, параллельную оси ОХ. В пересечении проведенных направлений определится точка e. Из плана ускорений определяем величины абсолютных ускорений точек и касательных составляющих, которые необходимы для определения угловых ускорений звеньев. аВ=b·А=86·0,1=8,6м/с 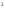 , аД=d·А=64·0,1=6,4м/с2, , аД=d·А=64·0,1=6,4м/с2,аЕ=e·А=107·0,1=10,7м/с2, aBA=nBАb·А=108·0,1=10,8м/с2, aBC=nBCb·А=62·0,1=6,2м/с2, аЕД 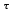 = nEDe·А=52·0,1=5,2м/с2. = nEDe·А=52·0,1=5,2м/с2.Определяем угловые ускорения звеньев 2, 3 и 4. 2=aBA/lAB =10,8/0,35=30,9c-2; 3 = aBC/lBC=6,2/0,4=15,5c-2; 4 = aED/lED =5,2/0,35=14,9c-2. Для определения направления углового ускорения звена необходимо вектор касательного ускорения мысленно с плана ускорений перенести параллельно самому себе на план механизма в точку, стоящую в индексе при а на первом месте. Результаты вычислений заносим в табл. 2. Таблица 2 - Значения линейных ускорений точек и угловых ускорений звеньев механизма
На звеньях 2, 3 и 4 в каждом положении наносим направления угловых скоростей и ускорений. 2 Анализ зубчатого механизма Исходные данные: 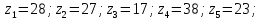 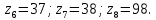 2.1 Определение передаточного отношения графическим методом Изображаем в масштабе зубчатый механизм, приняв произвольное стандартное значение модуля (m = 1,5 мм). Диаметры колес при этом находятся по формуле 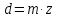 , ,где d – диаметр зубчатого колеса, мм, m – модуль колеса, мм, z – число зубьев. Для определения передаточного отношения графическим методом изображаем заданный механизм в масштабе, приняв произвольное значение модуля. Обозначим на механизме все характерные точки – полюса зацеплений и центры колес. Проводим линию, перпендикулярную осям вращения колес и на нее проецируем все характерные точки. Так как ведущим звеном является колесо 1, то изображаем линейную скорость его конца (точка А) вектором Аа произвольной длины. Соединив точки а и О1, получаем линию распределения линейных скоростей первого колеса. Соединяем точки а и О2-3, и проецируем т.В на эту линию. Получили линию распределения линейных скоростей 2 и 3 колес. Соединяем т.b с т О4, получаем линию распределения линейных скоростей 4 колеса. На продолжение этой линии проецируем т.С. Получили линию распределения линейных скоростей 4 и 5 колес. Соединяем т.с с т.D, получаем линию распределения линейных скоростей сателлитов 6 и 7. На эту линию проецируем т. О6-7. И соединяем О6-7 с т. ОН получаем линию распределения конечного звена – водила. Передаточное отношение определится через отрезки S1 и SН 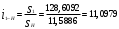 . .2.2 Определение передаточного отношения аналитическим методом Для определения передаточного отношения аналитическим методом разбиваем весь зубчатый механизм на две части. Первая часть со звеньями 1,2,3,4 – представляет собой ступенчатый ряд. вторая часть со звеньями 5,6,7,Н,8 – представляет собой собственно-планетарный механизм. 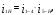 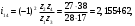 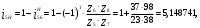 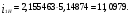 Вычисляем относительную ошибку  i = i = 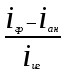 100% = 100% = 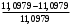 100%= 0%. 100%= 0%.2.3 Проверка выполнения условий соосности, соседства и сборки планетарного механизма Условие соосности представляет равенство межцентровых расстояний пар зубчатых колес r8 – r7 = r5 + r6 или z8 – z7 = z5 + z6 98 – 38 = 23 + 37 60 = 60 Условие соосности выполняется. Условие соседства определяет возможность размещения всех сателлитов по окружности их центров без задевания друг за друга. 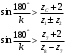 , ,где k–число сателлитов; zc - число зубьев большего из сателлитов. При k = 4 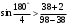 , ,0,707 > 0,667. Условие соседства выполняется. Для данной схемы планетарного механизма условие сборки выполняется при выполнении условия соосности. Условие сборки выполняется. Таким образом, планетарная часть заданного зубчатого механизма удовлетворяет всем требованиям проектирования. 3 Расчет маховикаИсходные данные: схема механизма  lOA=0,27 м, lAB=0,58 м, lAS=0,19 м, d=0,11 м, 1=60 с-1, J1=0,011кг∙м2, J2=0,023 кг∙м2, m2=2,3 кг, m3=2,2 кг, =0,16, Pimax=240000 Па, диаграмма 9. Требуется определить момент инерции маховика по методу избыточных работ рассчитать геометрические параметры маховика, его массу и вычертить эскиз. Строим план механизма при произвольном положении кривошипа в масштабе l = lOA/OA =0,27/50=0,0054 м/мм. Тогда АВ = 107,41 мм, AS = 35,19 мм. Строим восемь совмещенных планов механизма (через 45° угла поворота кривошипа). Поверх их накладываем повернутые на 90° планы скоростей в масштабе V = l1 = 0,0054∙60 = 0,324 (м/с)/мм . Строим индикаторную диаграмму и определяем её масштаб Pi = pimax/ypimax = 240000/200 = 1200 Па/мм, где yмах - максимальная ордината индикаторной диаграммы, мм. Проецируя крайние точки диаграммы вниз, на оси абсцисс получаем точки 1, 5' . Из точки 1 под произвольным углом проводим прямую и откладываем на ней отрезок 1-5, равный ходу ползуна (на плане механизма), откладываем на нем промежуточные точки 2, 3, 4, 6, 7, 8. Соединив точки 5 и 5', получаем масштабный треугольник, используя который, определяем значения индикаторного давления для различных положений угла поворота кривошипа. Из плана механизма, повернутых планов скоростей и индикаторной диаграммы составляем таблицу значений исходных данных для расчета на компьютере. Таблица 3 – Исходные данные для расчета
где X = Pbi, H = aibi – отрезки с планов скоростей в миллиметрах; aisi - расстояния расположения точек si, находим по теореме подобия aisi = aibi  AS / АВ; AS / АВ;S = Psi – расстояния между точками P и si с плана скоростей в миллиметрах; Y = Pi - индикаторное давление в паскалях. Дополнительные данные для расчета: 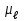 = 0,0054 м/мм – масштаб плана механизма; = 0,0054 м/мм – масштаб плана механизма;d = 0,11 м – диаметр поршня; 1 = 60 с-1 – угловая скорость кривошипа; J1 = 0,011 кг∙м2 – момент инерции кривошипа; J2 = 0,023 кг∙м2 – момент инерции шатуна; AB = 107,41 мм – длина шатуна на плане механизма; m2 = 2,3 кг – масса шатуна; m3 = 2,2 кг – масса поршня. Рассчитываем на компьютере значения приведенного момента движущих сил Мпр и кинетической энергии звеньев механизма Тзв по формулам 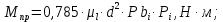 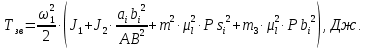 Результаты расчета представлены в приложении А. По результатам расчетов строим график приведенного момента от движущих сил в функции угла поворота кривошипа в масштабах: Мпр = Мпрмах/уМпрмах = 563,47/102,45 = 5,5 Н∙м/мм; = /x = 2/160 = 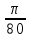 рад/мм. рад/мм.Принимаем условие, что при такте расширения совершается полезная работа, поэтому график Мпр( 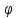 ) для первых четырех положений располагается выше оси абсцисс, а для остальных четырех - ниже. ) для первых четырех положений располагается выше оси абсцисс, а для остальных четырех - ниже. Графически интегрируя график Мпр = Мпр ( 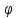 ), получаем график работы движущих сил Адв=Адв( ), получаем график работы движущих сил Адв=Адв(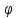 ). При этом произвольно принимаем расстояние от начала координат до полюса интегрирования h=45 мм. ). При этом произвольно принимаем расстояние от начала координат до полюса интегрирования h=45 мм. Учитывая, что при решении задачи расчета маховика рассматривается цикл установившегося неравновесного движения, график работы сил полезного сопротивления Ас = Ас( 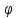 ) получаем в виде отрезка, соединяющего начало и конец графика работы движущих сил. ) получаем в виде отрезка, соединяющего начало и конец графика работы движущих сил.Масштаб полученных графиков определится: А = Мпрh = 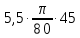 = 9,73 Дж/мм. = 9,73 Дж/мм.График изменения кинетической энергии - ∆Т = ∆Т() получаем как разность ординат графиков Адв() и Ас(), т.е ∆Т = Адв – Ас. В этой же системе координат по результатам расчетов вычерчиваем график изменения кинетической энергии звеньев механизма – Тзв = Тзв() с учетом Тзв=Т=А. Вычитая ординаты графика Тзв = Тзв() из ординат графика ∆Т = ∆Т() получаем график изменения энергии маховика Тм = ∆Т – Тзв. Проекции точек, соответствующих максимальному и минимальному значениям Тм , на ось ординат дадут отрезок (cd), по которому определяем момент инерции маховика JМ = cdT/(12)= 75,8∙9,73(0,16∙602)=1,28кг∙м 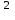 Диаметр обода маховика De определяем из условия, что для стальных маховиков окружная скорость не должна превышать 110 м/с Dе 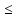 2Vд/1 2Vд/1 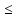 2110/60 = 3,667 м. 2110/60 = 3,667 м.Из конструктивных соображений принимаем диаметр Dе = 0,45 м. Внутренний и внешний диаметры обода маховика определяем по выражениям Di = 0,85De = 0,38 м, Dcp = (De + Di)/2 = 0,415 м. Определяем массу маховика и ширину его обода m = 4JM/Dcp2 = 41,28/0,415 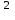 = 29,7 кг. = 29,7 кг.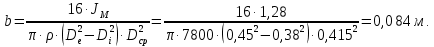 где = 7800 кг/м 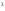 - плотность материала. - плотность материала.Вычерчиваем эскиз маховика. Курсовой проект выполнил: __________________ Чураков В.Э. Дата, подпись Литература1 Овчинников В.А. Курсовое проектирование по теории механизмов и машин. – Киров: Вятская ГСХА, 2000. – 173 с. 2 Овчинников В.А. Теория механизмов и машин. Курс лекций: Учебное пособие. – Киров: Вятская ГСХА, 2008. – 231 с. Приложение А (обязательное) Результаты расчета маховика 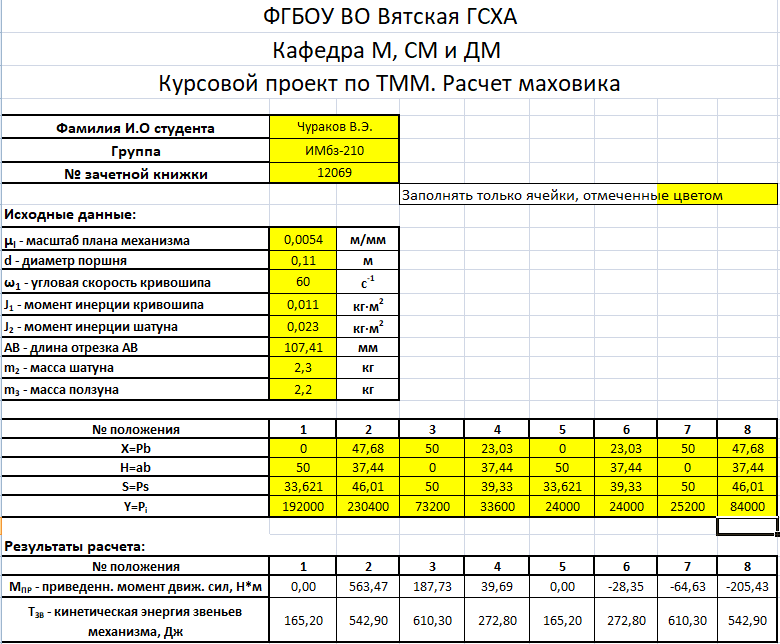 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
