Курсовая. Квадратурные методы вычисления определенных интегралов
 Скачать 145 Kb.
|
|
Курсовая работа на тему: Квадратурные методы вычисления определенных интегралов. Введение. Задача вычисления интегралов возникает во многих областях прикладной математики. В большинстве случаев встречаются определённые интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определёнными интегралами, сами подынтегральные функции не являются элементарными. Распространенными являются также случаи, когда подынтегральная функция задается графиком или таблицей экспериментально полученных значений. В таких ситуациях используют различные методы численногоинтегрирования, которые основаны на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью. Пусть требуется вычислить интеграл 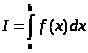 при условии, что a и b конечны и f(x) является непрерывной функцией на всем интервале (a, b). Значение интеграла I представляет собой площадь, ограниченную кривой f(x),осью x и прямыми x=a, x=b (Рис.1). Вычисление I проводится путем разбиения интервала от a до b на множество меньших интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок.1. Общая постановка и анализ задачи. 1.1. Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида 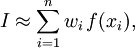 где  — число точек, в которых вычисляется значение подынтегральной функции. Точки  называются узлами метода, числа  — весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.Требуется найти определенный интеграл I = по квадратурной формуле Чебышева. Рассмотрим, что представляет из себя вообще квадратурная формула, и как можно с ее помощью вычислить приближенно интеграл. Известно, что определенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= Криволинейная трапеция. Если f(x) непрерывна на отрезке [a, b], и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по, известной всем, формуле Ньютона - Лейбница = F(b) - F(a) где F’(x) = f(x) Однако во многих случаях F(x) не может быть найдена, или первообразная получается очень сложной для вычисления. Кроме того, функция часто задается таблично. Поэтому большое значение приобретает приближенное и в первую очередь численное интегрирование. Задача численного интегрирования состоит в нахождении приближенного значения интеграла по заданным или вычисленным значениям подинтегральной функции f(x) в некоторых точках ( узлах ) отрезка [ a, b]. Численное определение однократного интеграла называется механической квадратурой, а соответствующие формулы численного интегрирования - квадратурными . Заменяя подинтегральную функцию каким-либо интерполционным многочленом, мы получим квадратурные формулы вида, где xk - выбранные узлы интерполяции; Ak - коэффициенты, зависящие только от выбора узлов, но не от вида функции (k=0,1,2,........, n). R - остаточный член, или погрешность квадратурной формулы. Отбрасывая остаточный член R, мы совершаем погрешность усечения. При расчете к ней добавляются еще различные погрешности округления. Разобьем отрезок интегрирования [a, b] на n равных частей системой точек xi= xo+ i..h; ( i = 0,1,2,......,n) xo= a; xn= b; h= (b-a)/n ; и вычислим подинтегральную функцию в полученных узлах yi= f(xi) ; ( i = 0,1,2,......,n) Количество параметров квадратурного выражения тесно связано со степенью подынтегральной функции, если последняя может быть описана степенным полиномом ограниченной степени. В общем случае это невозможно, например, когда подынтегральная функция терпит разрыв. Для устранения особенности интегрируемой функции, последнюю представляют произведением весового сомножителя, включающего в себя характерную особенность, и части подынтегральной функции, которая после исключения особенности может представляться степенным многочленом. Возможность представления подынтегральной функции полиномом позволяет оценить минимально необходимое число параметров в квадратурной формуле, исходя из критерия получения по ней абсолютно точного значения интеграла. Так, для подынтегральной функции, представленной полиномом нулевой степени, вычисление площади в интервале [a, b] достаточно одного значения функции (площадь прямоугольника). Для полинома первой степени - два значения (площадь трапеции). Для второй степени - три, и т.д. Последнее следует из того, что через (n+1) точку можно провести единственную кривую n-й степени. Параметрами квадратурных формул являются коэффициенты при значениях полиномиальной подынтегральной функции и значения независимой переменной, при которых вычисляется подынтегральная функция. где - параметры квадратурной формулы,- функция с выделенной особенностью,- весовая функция, включающая особенность.Для подынтегральных функций без особенностей p (x) =1.Квадратурные формулы строятся для пределов интегрирования и . Замена пределов интегрирования на или осуществляется линейным преобразованием, которое выше было уже рассмотрено. Построение любой квадратурной формулы начинается с решения вопроса о классе подынтегральных функций, для которых формула будет абсолютно точна. Если выбраны функции степенного базиса, то число параметров, которое необходимо ввести в квадратурную формулу, равно наивысшей степени n базисной функции, увеличенной на единицу. Если точки, в которых вычисляются значения подынтегральной функции, определены условиями удобного положения или простотой вычисления в них, то в квадратурной формуле число слагаемых будет равно числу параметров. Если положения точек тоже взяты в качестве параметров, то число слагаемых может оказаться и вдвое меньше. В квадратурную формулу можно ввести также значения производных подынтегральной функции в заданных точках, если вычисление производных проще, чем вычисление функции. Когда все условия построения квадратурной формулы оговорены, то, используя метод неопределенных коэффициентов (параметров), составляют систему алгебраических уравнений путем подстановки в интеграл и квадратурную формулу базисных функций. Так как число их равно числу параметров, то система будет определена.1.2. Вывод формул численного интегрирования с использованием интерполяционного полинома Лагранжа Пусть для y=f(x) известны в n+1 точках X0,X1,X2..Xn промежутка [a,b] соответствующие значения f(xi)=yi (i=0,1,2..n). Требуется приближенно найти По заданным значениям Yi построим полином Лагранжа. Заменим f(x) полиномом Ln(x). Тогда где Rn(f) – ошибка квадратурной формулы. Отсюда, воспользовавшись выражением для Ln(x), получаем приближенную квадратурную формулу: Для вычисления коэффициентов Аi заметим что: 1.коэффициенты Ai при данном расположении узлов не зависит от выбора функции f(x); 2.для полинома степени n последняя формула точная. Пологая y=xK (k=0,1,2..,n), получим линейную систему из n+1 уравнений: где (k=0,1,..,n), из которой можно определить коэффициенты А0,А1,..,АN. Определитель системы есть определитель Вандермонда Заметим, что при применении этого метода фактическое построение полинома Лагранжа Ln(x) является излишним. Простой метод подсчета погрешности квадратурных формул разработан С.М. Никольским. Теперь рассмотрим несколько простейших квадратурных формул. В качестве примера найдем квадратурную формулу с тремя плавающими узлами для функций , принадлежащих множеству , где n=5.Формула должна иметь 3 слагаемых с шестью параметрами. Интервал интегрирования возьмем .где - неизвестные весовые коэффициенты,- неизвестные узловые точки, в которых должнавычисляться подынтегральная функция.Вычисляются определенные интегралы для множества базисных функций:Подстановка базисных функций в выражение с параметрами и их приравнивание соответствующим значениям интегралов от базисных функций приводит к следующей системе нелинейных уравнений:Решение таких уравнений основано на существовании двух канонических форм записи нулей степенных уравнений:где - коэффициенты, выражаемые через корни .И первая и вторая формы обращаются в нуль, если .Чтобы выделить из системы уравнений узловые многочлены, умножим первые 4 уравнения системы на коэффициенты из левой колонки и найдем их сумму, затем умножим соответствующие уравнения на среднюю колонку и найдем их сумму и, наконец, - на правую колонку и тоже просуммируем: Все взятые в круглые скобки узловые многочлены обязаны быть равными нулю, так как в них подставлены значения узлов , в которых многочлен обязан обращаться в нуль. Поэтому правые части уравнений равны нулю и после подстановки в левые части числовых значений для получается система линейных алгебраических уравнений относительно пока неизвестных констант :Корни легко находятся и равны следующим значениям:.Теперь остается найти весовые коэффициенты, для чего в первые 3 уравнения подставим найденные значения узловых точек:. Отсюда: .В результате квадратурная формула наивысшей алгебраической степени точности приняла следующий окончательный вид:Оценить погрешность квадратурной формулы можно, если в этих же пределах проинтегрировать отбрасываемую часть разложения в ряд Тейлора подынтегральной функции. Первые n членов ряда определяют максимальную степень базисных функций, а значит, и алгебраическую степень точности полученной на их основе формулы.Прежде, чем перейти к формуле прямоугольников, сделаем следующее замечание: З а м е ч а н и е. Пусть функция f(x) непрерывна на сегменте [a, b], а  - некоторые точки сегмента [a, b]. Тогда на этом сегменте найдётся точка  такая, что среднее арифметическое    .В самом деле, обозначим через m и M точные грани функции f(x) на сегменте [a, b]. Тогда для любого номера k справедливы неравенства  . Просуммировав эти неравенства по всем номерам  и поделив результат на n, получим Так как непрерывная функция принимает любое промежуточное значение, заключённое между m и M, то на сегменте [a, b] найдётся точка такая, что .Первые формулы для приближенного вычисления определённых интегралов проще всего получаются из геометрических соображений. Определенный интеграл 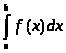 есть площадь некоторой фигуры, ограниченной кривой на [a,b], ставится задача об определении этой площади.Прежде всего, нужно разбить фигуру (рис. 2) на полоски, скажем, одной и той же ширины , а затем каждую полоску приближенно заменить прямоугольником, за высоту которого принята какая-либо из ее ординат. Это приводит нас к формуле 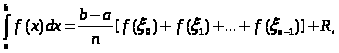 (1)где   , а R – дополнительный член. Здесь искомая площадь криволинейной фигуры заменяется площадью некоторой состоящей из прямоугольников ступенчатой фигуры (или – если угодно – определенный интеграл заменяется интегральной суммой). 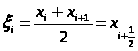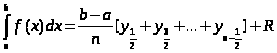Эта формула и называется формулой прямоугольников.На практике обычно берут  ; если соответствующую среднюю ординату  обозначить через  , то формула перепишется в виде .2.1.1. Дополнительный член в формуле прямоугольников. Перейдём к отысканию дополнительного члена в формуле прямоугольников. Справедливо следующее утверждение: У т в е р ж д е н и е. Если функция f(x) имеет на сегменте [a, b] непрерывную вторую производную, то на этом сегменте найдётся такая точка  , что дополнительный член R в формуле (1) равен (2)Доказательство. Оценим 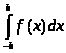 , считая, что функция f(x) имеет на сегменте [-h, h] непрерывную вторую производную Для этого подвергнем двукратному интегрированию по частям каждый из следующих двух интегралов: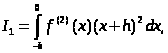 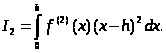 Для первого из этих интегралов получим 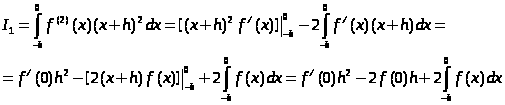 Для второго из интегралов аналогично получим Полусумма полученных для 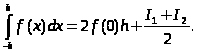 и  выражений приводит к следующей формуле: (3)Оценим величину  , применяя к интегралам и формулу среднего значения и учитывая неотрицательность функций  и  . Мы получим, что найдутся точка  на сегменте [-h, 0] и точка  на сегменте[0 ,h] такие, что В силу доказанного замечания на сегменте [-h, h] найдётся точка такая, что  Поэтому для полусуммы мы получим следующее выражение: Подставляя это выражение в равенство (3), получим, что 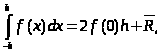 (4)где   . (5)Так как величина 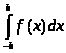 представляет собой площадь некоторого прямоугольника с основанием  (рис.1), то формулы (4) и (5) доказывают, что ошибка, совершаемая при замене указанной площадью, имеет порядок  Таким образом, формула 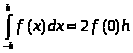 тем точнее, чем меньше h. Поэтому для вычисления интеграла 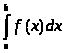 естественно представить это интеграл в виде суммы достаточно большого числа n интегралов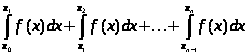 И к каждому из указанных интегралов применить формулу (4). Учитывая при этом, что длина сегмента равна  , мы получим формулу прямоугольников (1). При этом воспользовавшись формулой, доказанной в утверждении, для функции  и учитывая что,  получим дополнительный член в формуле прямоугольников 1.3 Формула трапеций и средних прямоугольников. Метод трапеций Если функцию на каждом из частичных отрезков представить прямой, проходящей через конечные значения, то получим метод трапеций. Пусть требуется вычислить интеграл 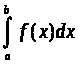 , где f(x) - непрерывная функция на [a,b]. Для простоты рассуждений ограничимся случаем, когда f(x)0. Разобьем отрезок [a, b] на n отрезков точками a=x0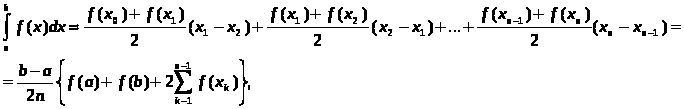 Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты. Таким образом, получена приближенная формула 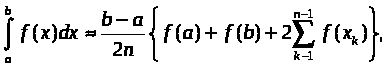 которая и называется формулой трапеций. Эта формула тем точнее, чем больше n. Погрешность формулы трапеций:  где  Заменим дугу АВ стягивающей ее хордой, получим прямолинейную трапецию аАВb, площадь которой примем за приближенное значение интеграла 0 a b x Метод средних прямоугольников. По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей — для метода трапеций: , для метода средних прямоугольников: . 1.4. Общая формула Симпсона (параболическая формула) Пусть n=2m есть четное число и yi=f(xi) (i=0,1,2...n) - значения функции y=f(x) для равноотстоящих точек а=x0,x1, ... ,xn=b с шагом Применив формулу Симпсона к каждому удвоенному промежутку [x0,x2], [x2,x4] ... [x2m-2,x2m] длины 2h и введя обозначения s1=y1+y2+ ... +y2m-1 s2=y2+y4+ ... +y2m получим обобщенную формулу Симпсона: Остаточный член формулы Симпсона в общем виде: где xk I (x2к-2,x2к) Формула Симпсона Если для каждой пары отрезков построить многочлен второй степени, затем проинтегрировать его на отрезке и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона. В методе Симпсона для вычисления определенного интеграла весь интервал интегрирования [a,b] разбивается на подинтервалы равной длины h=(b-a)/n. Число отрезков разбиения является четным числом. Затем на каждой паре соседних подинтервалов подинтегральная функция f(x) заменяется многочленом Лагранжа второй степени (рисунок 5). Рис. 5 Функция y=f(x) на отрезке заменяется многочленом 2-го порядка Рассмотрим подынтегральную функцию на отрезке . Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с y= в точках : Проинтегрируем на отрезке .: Введем замену переменных: Учитывая формулы замены, Выполнив интегрирование, получим формулу Симпсона: Полученное для интеграла значение совпадает с площадью криволинейной трапеции, ограниченной осью , прямыми , и параболой, проходящей через точки На отрезке формула Симпсона будет иметь вид: В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3, ..., х2n-1 имеет коэффициент 4, в четных точках х2, х4, ..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, хn =b - коэффициент 1. Геометрический смысл формулы Симпсона: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами. Если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем где М - наибольшее значение на отрезке [a, b]. Так как n4 растет быстрее, чем n2, то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций. Пример Вычислим интеграл Этот интеграл легко вычисляется: Возьмем n равным 10, h=0.1, рассчитаем значения подынтегральной функции в точках разбиения , а также полуцелых точках . По формуле средних прямоугольников получим Iпрям=0.785606 (погрешность равна 0.027%), по формуле трапеций Iтрап=0.784981 (погрешность около 0,054. При использовании метода правых и левых прямоугольников погрешность составляет более 3%. Для сравнения точности приближенных формул вычислим еще раз интеграл , но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках: у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000. По формуле Симпсона получаем Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f(4)(x)=24/(1+x)5 , откуда следует, что на отрезке [0, 1] . Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880 44)=0.0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций. 1.5. Квадратурная формула Чебышева Использовав три точки отрезка интегрирования можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. Докажем предварительно две леммы. Лемма 1.1. Через любые три точки М1 (х1; у1), М2 (х2; у2), М3 (х3; у3) с различными абсциссами можно провести единственную кривую вида у=Ах2+Вх+С (1) Доказательство. Подставляя в уравнение параболы (1) координаты точек М1 , М2 , М3 , получаем систему трех уравнений первой степени с тремя неизвестными А, В, С: 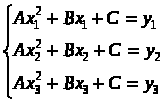 Так как числа х1, х2, х3 различны, то определитель этой системы отличен от нуля: 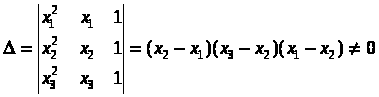 Следовательно, данная система имеет единственное решение, т.е. коэффициенты А, В, С определяются однозначно. Отметим, что если А0, то кривая (1) является параболой, если А=0, то прямой. Лемма 1.2. Площадь s криволинейной трапеции, ограниченной кривой у=Ах2+Вх+С, проходящей через точки М1 (-h; y1), M2 (0, y2), M3 (h, y3) (рис. 2) выражается формулой 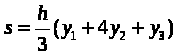 (2)Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что 2Аh2+2С=у1+у3; С=у2 (3) Учитывая соотношение (3), имеем 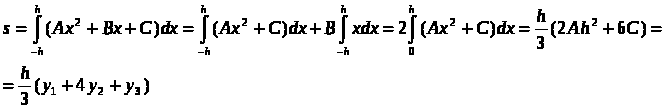 Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2 равных отрезков точками a=x0 Через каждую тройку точек М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей «параболической» трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)] 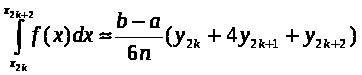 где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу 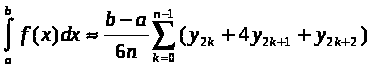 или в развернутом виде 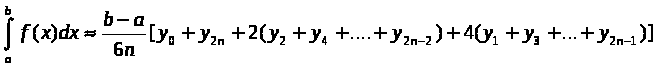 Эта формула называется формулой парабол или формулой Симпсона. В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3, ..., х2n-1 имеет коэффициент 4, в четных точках х2, х4, ..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, х1, х2n =b - коэффициент 1. Геометрический смысл формулы Симпсона очевиден: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами (прямыми). В высшей математике доказывается, что если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем 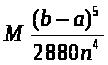 где М - наибольшее значение 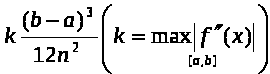 на отрезке [a, b]. Выше отмечалось, что погрешность формулы трапеций оценивается числом Так как n4 растет быстрее, чем n2, то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций. Этим и объясняется, что формула Симпсона позволяет получить большую точность, чем формула трапеций. Рассмотрим квадратурную формулу вида: функцию f(x) будем исать в виде когда f(x) многочлен вида f(x)=ao+a1x+...+anxn . Проинтегрировав, преобразовав и подставив значения многочлена в узлах f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n . . . . . . . . . . . . . . . . f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn получим формулу Чебышева. Значения х1,х2,..,хn для различных n приведены в таблице 3. Значения х1,х2,..,хn для различных n. где a=0 ; b= ; при n=5; f(x) = sin(x); x2= p/4+p/4*t2=p/4+p/4(-0,374341)=0,490985 x3= p/4+p/4*t3=p/4+p/4*0=0,785 x4=1- x2=1-0,490985 = 0,509015 x5=1- x1=1-0,131489=0,868511 y1=sin(x1) = sin(0,131489)=0,131118 y2=sin(x2) = sin(0,490985)=0,471494 y3=sin(x3) = sin(0,785)=0,706825 y4=sin(x4) = sin(0,509015)=0,487317 y5=sin(x5) = sin(0,868511)=0,763367 I = p/10(0,131118+0,471494+0,706825+0,487317+0,763367) = =p/10*2,560121=0,8038779. 3. Описание программы Integral. pas. Алгоритм. Процедура VVOD - заполняет массив, содержащий в себе аргументы xi Процедура FORM - используя массив, содержащий аргументы xi заполняет массив yi Процедура CHEB - используя массивы xi и yi, высчитывает по квадратурной формуле Чебышева приближенное значение интеграла. Процедура TABL - это подпрограмма, осуществляющая вывод таблицы узлов (аргумент - функция) При запуске программы нужно ввести границы интегрирования. После ввода границ интегрирования используется процедура VVOD, а затем высчитывается и выводиться на экран шаг табулирования функции h. После этого используем процедуры FORM и CHEB . Получив результат, выводим таблицу ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же очень важно то, какой будет взят шаг интегрирования. Хотя численные методы и не дают очень точного значения интеграла, но они очень важны, так как не всегда можно решить задачу интегрирования аналитическим способом. Листинг программы. Программа написана на языке Tubro Pascal 7.0 для MS-DOS. Ниже приведен ее листинг: program integral; uses crt; const n=5; k=-0.832498; l=-0.374541; z=0.0; type aa=array[1..n] of real; var x,y:aa; a,b,h,ich:real; { заполнение х-сов в массив х[5] } procedure vvod(var a,b:real;var c:aa); var i:integer; t:aa; Begin t[1]:=k; t[2]:=l; t[3]:=z; t[4]:=l; t[5]:=k; for i:=1 to n-1 do c[i]:=((b+a)/2+(b-a)/2*t[i]); for i:=n-1 to n do c[i]:=1 - c[n+1-i]; end; { заполнение y-ков в массиве у[5] } procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; { процедура для расчета интеграла по квадратурной формуле Чебышева } procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich:=0; for i:=1 to n do ich:=ich+y[i]*h; end; { процедура вывода таблицы} procedure tabl; var i:integer; Begin writeln(' ___________________________________ '); writeln('| i | t| x|y |'); writeln(' ___________________________________ '); writeln('| 1 |',k:9:6,'|',x[1]:9:6,' |',y[1]:9:6,'|'); writeln('| 2 |',l:9:6,'|',x[2]:9:6,' |',y[2]:9:6,'|'); writeln('| 3 |',z:9:6,'|',x[3]:9:6,' |',y[3]:9:6,'|'); writeln('| 4 |',l:9:6,'|',x[4]:9:6,' |',y[4]:9:6,'|'); writeln('| 5 |',k:9:6,'|',x[5]:9:6,' |',y[5]:9:6,'|'); writeln(' ___________________________________ '); end; Begin clrscr; writeln(' П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я'); writeln(' О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А '); writeln; writeln('Введите границы интегрирования a,b:'); readln(a,b); vvod(a,b,x); h:=(b-a)/n; writeln('h=',h:9:6); form(x,y); cheb(y,ich); tabl; writeln('I=',ich:8:6); end. 6. Приложения 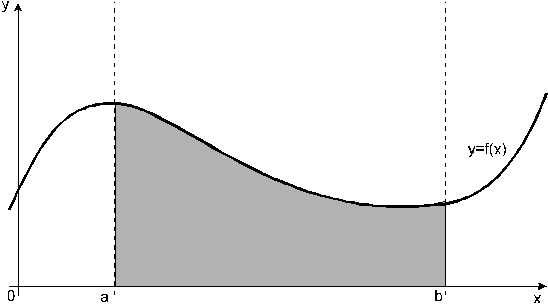 Рис. 1. Криволинейная трапеция. Р 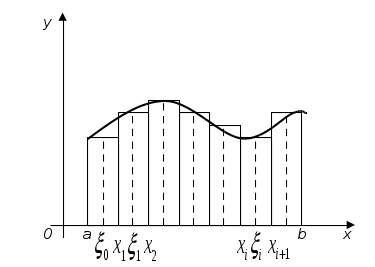 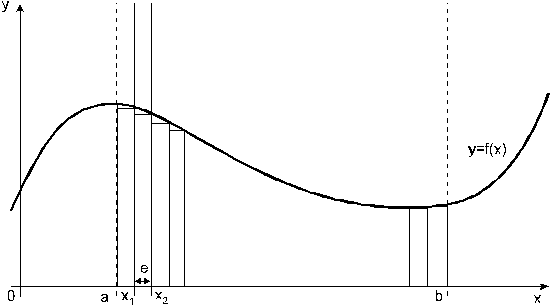  Вывод результата : П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А Введите границы интегрирования a,b: 0 1.5708 h= 0.314160 ____________________________ | i | t | x | y | ____________________________ | 1 |-0.832498| 0.131556 | 0.131177| | 2 |-0.374541| 0.491235 | 0.471716| | 3 | 0.000000| 0.785400 | 0.707108| | 4 |-0.374541| 0.508765 | 0.487099| | 5 |-0.832498| 0.868444 | 0.763325| ____________________________ I=0.804383 Список литературы: 1. Ракитин Т.А., Первушин В.А. “Практическое руководство по численным методам с приложением программ на языке Basic“ 2. Крылов В.И. “Приближенные вычисления интегралов“ - М. : Физмат. 3. Демидович и Марон “Основы вычислительной математики“ 4. Копченова и Марон “Вычислительная математика в примерах и задачах” 5. Вольвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для ПЭВМ ЕС. Минск.: 1989 г. 6. Зуев Е.А. Язык программирования Turbo Pascal. М.1992 г. 7. Скляров В.А. Знакомьтесь: Паскаль. М. 1988 г. 1. Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 1: Учебное пособие для втузов (Глава XI, пп.8,9). 8. Ильин В. А., Куркина А. В. Высшая математика: учебник (Глава XIII, пп.7). 9. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления в 3-х томах, том II. (пп. 332, 335). 10. Ильин В.А., Позняк Э.Г. Основы математического анализа, часть I. Москва «Наука», 1982г. (Глава 12, пп.1, 2, 5). |