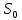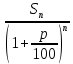Экономические задачи. Диплом Кирилл. Квалификационная работа методика обучения решению экономикоматематических задач в средней школе Работу
 Скачать 154.22 Kb.
|
|
Кроме указанных выше видов задач на простые проценты есть еще один - задачи на амортизационные отчисления. Для их решения используются знания по теме: «Арифметическая прогрессия». Использования этого вида задач на уроках алгебры в 9-ом классе позволяет не только разнообразить круг задач, решаемых школьниками, но и указать на прикладной характер арифметической прогрессии. Задача 7. Предприятие приобрело универсальный станок за 320 тыс.р. Срок службы станка — 8 лет, после чего он реализуется по остаточной стоимости 50 тыс.р., Составьте таблицу уменьшения стоимости по годам, если уменьшение стоимости станка происходит равномерно. На сколько процентов уменьшится стоимость станка к концу 5-го года? Решение: этап. Предмет исследования - вычисление ежегодных амортизационных отчислений. Цель исследования — определение величины амортизационных отчислений и стоимости оборудования на конец заданного периода. этап. Структурные элементы, описывающие данную экономическую ситуацию: первоначальная стоимость оборудования; конечная стоимость оборудования; срок службы оборудования; величина ежегодных амортизационных отчислений. этап. Если уменьшение стоимости оборудования происходит равномерно, то амортизационные отчисления равны отношению разности первоначальной и конечной стоимостей оборудования к сроку службы оборудования. этап. Обозначим через п — срок службы станка, через S— первоначальную стоимость станка, через Sn— остаточную стоимость станка, а через А - ежегодные амортизационные отчисления. Тогда амортизационные отчисления будут находиться по формуле:  5 этап. Полагая S= 320, п = 8,  = 50, получаемТаблица 5 Таблица уменьшения стоимости станка по годам
По окончанию 5-го года стоимость станка будет равна 151,25 тыс. р. Остаточные стоимости, представленные в табл. № 6, образуют арифметическую прогрессию с первым членом 320 и разностью -33,75. Это можно использовать для определения стоимости оборудования на конец какого-либо периода, не находя промежуточные значения. Одним из приложений простого процента в экономике является решение задач по налогообложению. По своему экономическому содержанию и математическому аппарату, используемому при их решении , они доступны, начиная уже с седьмого класса. Задача 8. Дана следующая условная схема налога на проценты: 8% с части дохода от 0 тыс. р. до 5 тыс. р. 12% с части дохода от 5 тыс. р. до 20 тыс. р. 16% с части дохода от 20 тыс. р. до 40 тыс. р. 22% с части дохода от 40 тыс. р. и выше. Предприниматель получил в качестве начисленных процентов сумму 41 тыс. р. Какой налог он должен уплатить? Чему равна в этом случае средняя ставка налога? Решение: этап. Предмет исследования - процесс налогообложения. Цель исследования - расчет средней ставки налога по предложенной схеме налогообложения. этап. Основные структурные элементы: налогооблагаемая сумма; процентная ставка; средняя ставка налога. этап. Для определения средней ставки налога налогооблагаемую сумму нужно разбить на части (каждая из которых соответствует предельной ставке налога) и рассчитать общую величину налога на проценты. этап. Если обозначим через S— всю сумму, а через S1, S2, ..., Sn— суммы, соответствующие предельным ставкам налога, через р1, р2, ..., рn— процентные ставки, a R- сумма налога, то:  +…+ Тогда для определения средней ставки налога достаточно сумму налога поделить на сумму начисленных процентов: 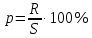 этап. Разобьем 41000 на части: 41000 = 5000 + 15000 + 20000 + 1000. Следовательно, 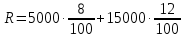 + +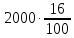 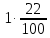Для определения р подставим полученную величину во вторую формулу: 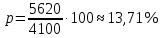 6 этап. Таким образом, если средняя ставка налога на проценты была бы неизменной и равной 13,71%, то величина налога на сумму 41 тыс. р. составила бы 5620 р. 2.2.2. Сложные проценты Разница между простыми и сложными процентами заключается в способе их начисления. Очень удобно объяснить сложные проценты с помощью экономических терминов. Процент является простым, если он начисляется только на исходную сумму, а сложным – если он начисляется на наращенный капитал, т.е. не только на основную сумму, но и на полагающиеся с неё проценты за предыдущий период. Мы уже указывали на то, что сложные проценты практически не рассматриваются на уроках математики, в любом, из рассмотренных нами, учебников математики это понятие отсутствует. Задач на их вычисление очень мало либо нет вообще. Это понятие можно встретить только в учебно-методических пособиях, предназначенных для подготовки к ЕГЭ, так как в российском ЕГЭ задание №17 является задачей с экономическим содержанием. До прошлого года и в Приднестровское ЕГЭ включалась аналогичная задача. Как было уже сказано, при решении математических задач с экономическим содержанием можно легко и доступно объяснить разницу между простыми и сложными процентами (между простым и сложным процентным ростом). Методика введения понятия сложного процента основывается на сравнении его с простым процентом. Если S0— первоначальная сумма, р — процентная ставка, выраженная в процентах, п — срок в годах, а 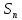 - наращенная сумма в конце п -го периода, тогда сумма в конце первого периода увеличилась до: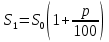 Так как в конце каждого периода сумма дохода прибавляется к основной сумме вклада, то сумма денежных средств по окончании п периодов рассчитывается по формуле: 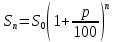 Эта формула предполагает выплату в конце каждого периода. Однако на практике часто встречаются ситуации, когда производятся дополнительные выплаты. Так, например, в течении года, выплаты могут производиться помесячно, т.е. 12раз в году. Для таких случаев вышеуказанную формулу следует изменить следующим образом: 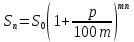 По этой формуле можно рассчитать сумму денежных средств по окончании п при т выплатах за период . Соотношение 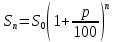связывает между собой такие величины как начальный вклад, годовую процентную ставку, срок хранения и наращенную сумму.Нижеприведенная таблица, в которой представлено выражение каждой из четырех величин, заимствована из книги А.С. Симонова [190, с. 78]. Таблица 6 Взаимосвязь компонентов формулы сложного процентного прироста
В следующей задачи покажем возможность использования указанных аналитических математических моделей сложных процентов, опуская первые три этапа математического моделирования, так как экономические ситуации, представленные текстом условия, нами рассмотрены были ранее. Задача 9. Какова наращенная сумма с вклада в 20 000 у.е., если вклад был положен на 6 лет под процентную ставку 25% годовых, при условии, что: а) ежегодного начисления процентов; б) ежеквартального начисления процентов. Решение: 4 этап. Для вычисления конченой суммы при условии ежегодного начисления сложных процентов будем использовать следующую модель: 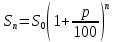а для ежеквартального 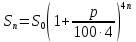 этап. а) Подставим в первую формулу известные величины, получим: 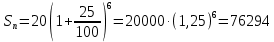 б) для ежеквартального начисления процентов, получим: 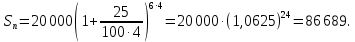 6 этап. В первом случае наращенная сумма будет равна 76294 у.е.., а во втором случае 85689 у.е. Следовательно, при увеличении количества выплат в течение периода наращенная сумма увеличивается. Введение сложных целесообразна начинать, решая задачи, в которых можно сравнить наращение вклада по схеме простых процентов и по схеме сложных. Их решение поможет ученикам увидеть разницу между простым и сложным процентным ростом, что в дальнейшем позволит более четко разделять эти понятия. Задача10. Рассчитайте наращенную сумму с исходной суммы вклада в 1000 тыс.р. при размещении ее в банк на условиях начисления простых и сложных процентов, если годовая процентная ставка равна 18%, а периоды наращения различны: 30 дней, 180 дней, 1 год, 3 года, 8 лет. В решении задачи полагать год равным 360 дням. Решение: Опускаем 1—4 этапы, так как модели начисления простых и сложных процентов были построены нами выше. 5 этап. Применяя формулы начисления простых и сложных процентов, при S0= 1000, р = 18 за различные периоды мы получим следующие результаты, для наглядности, представленные в табличном виде: Таблица 7 Начисления по формулам простых и сложных процентов
6 этап. Данная таблица помогает учащимся прийти к выводу о том, что если делается денежный вклад на срок менее одного года, то более выгодна схема простых процентов. Так, в частности, при сроке в 180 дней наращенная сумма составит: при использовании схемы простых процентов — 1 млн. 90 тыс. р., а при использовании схемы сложных процентов — 1 млн. 86 тыс. р., т.е. разница составит 4 тыс. р. Если срок размещения денежных средств превышает один год, ситуация изменяется: более выгодна становится схема начисления сложных процентов, причем наращение в этом случае идет более быстрыми темпами. Более наглядно это можно показать в графической форме: 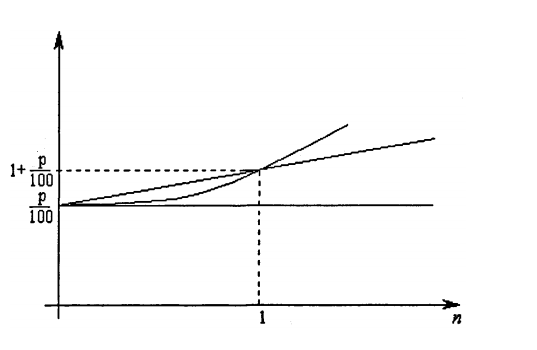 ВСТАВИТЬ РИСУНОК На рисунке приведены графики коэффициентов наращения в зависимости от срока п (в годах) для простых и сложных процентов при одинаковой годовой ставке р. Очевидно, что при п = 1 коэффициенты наращения совпадают и равны 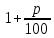 .Задачи такого рода наглядно демонстрируют необходимость интерпретирования и анализа результатов, полученных в ходе решения. Так в ходе решения выше рассмотренной задачи у учащихся создаётся положительная мотивация для исследовательской деятельности в ходе решения задач с экономико-математическим содержанием и закладывается умение видеть суть экономических ситуаций в дальнейшей жизни. Задача11. В банке получена ссуда в размере 40 тыс. долл. США на 8 лет на следующих условиях: для первых трех лет процентная ставка равна 28% годовых, на следующий год она увеличивается на 2%, и на последующие годы еще на 2,5%. Найдите сумму, которая должна быть возвращена банку по окончании срока ссуды при ежегодных начислениях сложных процентов. |
