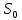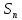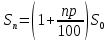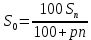Экономические задачи. Диплом Кирилл. Квалификационная работа методика обучения решению экономикоматематических задач в средней школе Работу
 Скачать 154.22 Kb. Скачать 154.22 Kb.
|
|
Глава 2. Методическое обеспечение обучения решению задач на уроках математики в средней школе 2.1. Использование задач с экономико-математическим содержанием на уроках математики в средней школе Задачи прикладного характера играют важную роль при изучении математических величин, объектов и понятий, их свойств и отношений между ними. Решение же прикладных задач с экономико-математическим содержанием способствует формированию экономической культуры и повышению финансовой грамотности учащихся. Кроме того, при решении задач с экономико-математическим содержанием, как и при любых других задачах прикладной направленности, учащиеся учатся строить математические модели реальных процессов, что приводит к более осмысленному восприятию окружающей действительности. Однако, не смотря на все выше указанные достоинства этих задач, как показывает анализ действующих учебников по математике и алгебре, в курсе математики практически нет прикладных задач, а задачи с экономическим содержанием в школьных учебниках, рекомендованных Министерством просвещения ПМР к использованию в общеобразовательных школах, практически отсутствуют. Кроме того, задачи, встречающиеся в школьных учебниках, в основном они не отражают реальную экономическую ситуацию, сложившуюся в современном мире. В нижеприведенной таблице № 1 отражено наличие задач прикладного (в частности, и экономико-математического) содержания в основных действующих учебниках алгебры VII-IX классов, действующих на территории ПМР. Таблица № 1 Данные из учебников математики относительно задач прикладного характера и задач с экономико-математическим содержанием
Как показывает анализ, количество прикладных задач, вообще, и с экономико-математическим содержанием, в частности, ничтожно мало. Но даже и в тех, что есть, не наблюдается адекватное отражение экономических реалий современного мира. При таких условиях говорить о возможности формирования экономической культуры учащихся невозможно. В связи с вышеизложенным возникает необходимость в составлении системы задач, которая могла бы соответствовать экономическим реалиям и при этом учитывать уровень владения соответствующим математическим аппаратом учащихся. С этой целью нами был проведен сравнительный анализ разделов элементарной математики, изучаемой в курсе основной школы, и разделов экономики, результаты которого приведены в таблице № 2. Таблица № 2 Использование экономико-математических задач при изучении курса математики в 7-9 классах
С нашей точки зрения, методически целесообразно в школьном курсе алгебры акцентировать внимание на задачах финансовой математики, так как, не смотря на всю ширину вопросов, которые она охватывает, соответствующий математический аппарат у школьников уже к VII классу сформирован. Покажем возможность применения задач данного вида, которые основаны на знании простых и сложных процентов. 2.2. Методические аспекты формирования у учащихся навыков решения экономико-математических задач Из раздела финансовой математики выбраны задачи, решение которых основано на применении знаний простых и сложных процентов. С понятием простого процента (или просто процента) учащиеся знакомятся в V-VI классах, однако, вопрос об использовании понятия сложного процента разработан недостаточно, во многих школьных учебных пособиях рассматриваются задачи, связанные с понятием сложного процента, однако, это в большинстве случаев происходит бессистемно и поверхностно. С понятием «процента» учащиеся впервые встречаются на уроках математики в V классе при изучении темы «Десятичные дроби». Они узнают, что 1% это одна сотая часть числа, т.е. процент – это одна из форм записи десятичной дроби. Кроме того (в зависимости от учебника, по которому ведется преподавание) в V или VI классах они учатся решать три типа задач на проценты: нахождение процента от числа, числа по его проценту и процентного соотношения. В школьных учебниках задач «на проценты» достаточно большое количество, но при этом, отрабатываются навыки применения процентов. Задач же со сложными процентами учащиеся почти не решают. Использование задач с экономико-математическим содержанием могло расширить область применения процентов. Например, это могут быть такие задачи как нахождение суммы вклада через определенный промежуток времени или задачи на кредитование, нахождение начальной или конечной суммы вклада при заданных условиях. Умение решать такие задачи не только бы повысило интерес к изучаемому предмету, но и понадобилось в дальнейшей жизни, так как практически каждому современному человеку приходится сталкиваться с такими экономическими понятиями, как начисление процентов, вклад, кредит. Полученные знания были бы хорошей основой для возможности верного анализа и принятия решений в будущем. Понятие сложных процентов, которое также используется в финансовой математике, можно рассматривать в IX классе при изучении таких тем, как «Арифметическая прогрессии» и «Геометрическая прогрессия». Представляется целесообразным, и дидактически оправданным включать задачи, содержащие простые и сложные проценты, при изучении различных разделов курса алгебры. Данные задачи не только обогащают стандартный набор текстовых задач, связывают математические методы и экономические понятия, расширяют кругозор учащихся, но и проигрывают реальные модели поведения в сложившейся экономической ситуации. 2.2.1. Простые проценты При рассмотрении некоторых математических задач с экономико-математическим содержанием можно продемонстрировать учащимся широту применения понятия простого процента, которое им известно уже с V класса. На основе этого понятия выводится формула (математическая модель) простого процентного роста. Наиболее понятные и доступные школьнику задачи, основанные на знании этой модели – являются задачи на депозиты. Поэтому знакомство с задачами с экономико-математическим содержанием рекомендуется начинать с задач начисления простого процента на вклады физических лиц. Например, следующая задача, вычисляющая будущую сумму вклада по схеме простых процентов, может использоваться при обучении уже в VII классе. Задача 3. Вкладчик открыл счет в банке на сумму в 3250 евро сроком на 2 года под простые проценты по ставке 7,8 % годовых. Какой будет сумма, которую вкладчик получит при закрытии вклада? На сколько вырастет вклад за два года? Чему равен коэффициент наращения? Решение: 1 этап. Предмет исследования — функционирование денежного капитала. Цель исследования — нахождение суммы вклада через заданный промежуток времени. 2 этап. Структурные элементы, соответствующие данной экономической ситуации: начальный вклад; годовая процентная ставка; способ начисления процентов - простые проценты; период вложения. 3 этап. Наращенная сумма получается путем сложения суммы начального вклада с соответствующим доходом, получаемым ежегодно. Так как указанная сумма зависит от времени, то нами будет простроена динамическая модель. 4 этап. Обозначим через S0— начальный вклад, р — процентную ставку, п — количество полных лет, Sn— сумма, полученную с начисленными процентами на конец п -го года. Тогда математическая модель функционирования вклада путем начисления простых процентов будет выглядеть следующим образом: 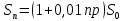 Данная формула является математической моделью ситуации, представленной текстом условия. 5 этап. Подставив соответствующие значения п = 2, р = 7,8, a S0= 3250, получаем 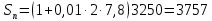 6 этап. Сумма вклада через 2 года будет равна 3757 евро, то есть вклад вырастет на 507 евро. Коэффициентом наращения простых процентов называют отношение 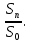 Он показывает, во сколько раз вырос первоначальный вклад S0за п лет хранения вклада по схеме простых процентов с годовой ставкой р %. Он показывает, во сколько раз вырос первоначальный вклад S0за п лет хранения вклада по схеме простых процентов с годовой ставкой р %.Исходя из данных текста условия и результата решения получаем, что этот коэффициент составляет 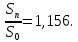 Данная экономико-математическая модель предлагается Замковым О.О. На ее основе можно составить учителю подобный ряд задач самостоятельно. В ходе педагогического эксперимента было установлено, что учащиеся испытывают трудности при выполнении первых трех этапов, но благодаря им школьники учатся применять методы ситуационного анализа, переходя от текста её условия к аналитической математической модели. Для самостоятельного построения системы задач, связанной с вычислением простого процентного роста можно использовать формулы, приведенные Симоновом А.С., которые выражают одну переменную через другую. [18] Также приведенную ниже таблицу можно заполнить вместе с учащимися при рассмотрении данного вида задач. Таблица 3 Взаимосвязь компонентов формулы простого процентного роста
В первой строке дана формула определения итоговой суммы по начальному вкладу, процентной ставке и количеству лет. Во второй – определение начального вклада по итоговой сумме, процентной ставке и количеству лет, в третьей – определение процентной ставки по начальной и итоговой суммам и количеству лети и, наконец, в четвертой - определение количества лет по начальной и итоговой суммам и процентной ставки. С нашей точки зрения, если ученики хорошо владеют знаниями о компонентах математических действий, то запоминать всю таблицу не имеет смысла. Любой неизвестный компонент из четырех можно вывести, зная три остальные. До этого мы рассматривали задачи, когда вклад находился в банке целое количество лет, но в жизни вкладчик может востребовать свой вклад и через 2, или через 3 месяца и 12 дней. Поэтому сучащимся будет интересно рассмотреть такие задачи, в которых количество лет не полное. Пусть годовая процентная ставка составляет 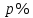 . Тогда за . Тогда за  часть года ставка составит часть года ставка составит 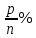 , а за , а за 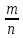 часть года составит часть года составит 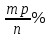 . .Отсюда следует, что, если банк начисляет р% годовых, то за один месяц он будет начислять 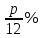 и за к месяцев величина вклада достигнет и за к месяцев величина вклада достигнет 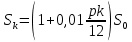 Если срок хранения выражается в днях, то очень важно знать, какое принято использовать количество дней в году и в каждом месяце. Например, в нашей стране и в России используется следующая система: предполагается, что длительность года составляет 360 дней, а длительность каждого месяца - 30 дней. Таким образом, если банк начисляет р% в год, то за один день он будет начислять 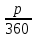 %. Тогда за к дней величина вклада составит: %. Тогда за к дней величина вклада составит: 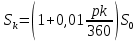 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||