Экономические задачи. Диплом Кирилл. Квалификационная работа методика обучения решению экономикоматематических задач в средней школе Работу
 Скачать 154.22 Kb. Скачать 154.22 Kb.
|
|
Решение: 4 этап. Разобьем весь срок на периоды равной годовой процентной ставки. В первый период идет начисление р1% годовых, длина периода — n1 лет, потом п2лет идет начисление р2% годовых, и в третий период продолжительностью п3года идет начисление р3% и т.д. Тогда за первый период будет начислена следующая сумма: 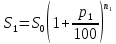 Тогда за второй и третий период соответственно: 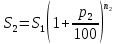 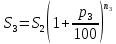 Значит, по прошествии 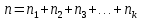 лет наращенная сумма будет равна: лет наращенная сумма будет равна: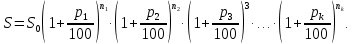 5 этап. В нашей задаче три периода. В первый период идет начисление 28% годовых, длина периода — 3 года, потом 1 год идет начисление 30%, и в третий период — 4 года — идет начисление 32,5%. Тогда за первый период будет начислена следующая сумма: S 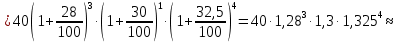 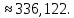 6 этап. Сумма возврата равна 336,122 тыс. долл. США с точностью до доллара. Одним из видов задач с экономико-математичеким содержанием, позволяющим не только овладевать математическими знаниями, но и повышать свою экономическую культуру, являются задачи на определение стоимости денег во времени. Стоимость денег во времени меняется. 1 рубль «сегодня» — это 1 рубль, который вложен «сегодня» под действующую ставку процента и который, следовательно, будет «завтра» и в дальнейшем иметь номинальную величину больше 1. Таким образом, 1 рубль «сегодня» - это вклад, который «завтра» станет равным по величине сумме первоначального вклада и процентов. То есть наряду с рассмотренными выше задачами экономистов интересует решение обратной задачи: какую сумму денежных единиц следует внести сегодня в банк по ставке р% годовых для того, чтобы через п лет накопить определенную сумму денежных единиц. Задача 12. Какую сумму нужно положить в банк под 12% годовых, чтобы через 3 года получить доход в 1000 долл. США? Решение: 1 этап. Предмет исследования — функционирование денежного капитала. Цель исследования — нахождение первоначального капитала. 2 этап. Структурные элементы, соответствующие данной экономической ситуации: наращенный капитал; годовая процентная ставка; способ начисления — сложные проценты; срок вложения. этап. Наращенная сумма получается путем сложения начальной суммы и дохода, полученного от вложения денег по схеме сложных процентов. этап. Модель данной экономической ситуации, выражена следующей формулой (взята из табл. № 7): 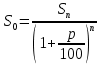 Подставим значения в формулу 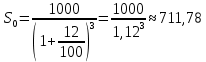 6 этап. Для накопления суммы в 1000 долл. США за 3 года по ставке 12% годовых вкладчику необходимо положить примерно 712 долл. США. Приложением сложных процентов в экономике также является дисконтирование. Дисконтирование - это процедура, определяющая сегодняшний аналог дохода, который может быть выплачен через определенный период при существующей норме процента. Основной вопрос дисконтирования при осуществлении различных проектов заключается в сопоставлении величины сегодняшних затрат с величиной будущих доходов. Задача 13. Землевладелец полагает, что сможет через 5 лет продать застройщику земельный массив площадью 80 га по цене 12 тыс. долл. США за гектар. Если не брать в расчет издержки по владению и продаже, то какая цена в денежном выражении, оплаченная сегодня, позволит землевладельцу получить накапливаемый ежегодный доход 12%? Решение: этап. Предмет исследования — текущая стоимость вложения. Цель исследования — определение стоимости на данный момент той единицы, которая будет получена в будущем. этап. Структурные элементы: первоначальная стоимость; срок вложения средств; процентная ставка дохода; сумма дохода. этап. Текущая стоимость вложения есть отношение будущей стоимости к начисленным процентам за весь период. этап. Модель, отражающая данную экономическую ситуацию, будет выглядеть следующим образом: 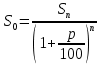 5 этап. Будущая стоимость данного участка земли равна 12*80 = 960 тыс. долл. США. Следовательно, 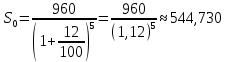 6 этап. Стоимость данного участка земли на данный момент составляет примерно 545 тыс. долл. США. Процесс нахождения сегодняшней стоимости платежа, осуществляемого через некоторое время, называется дисконтированием. На рассмотренном ниже примере можно объяснить следующую экономическую ситуацию — современную стоимость потока платежей (текущую стоимость аннуитета (ежегодной ренты), начинающихся с настоящего момента. Аннуитет - периодически выплачиваемые, равные по сумме денежные платежи в счет погашения полученного кредита и процентов по нему. Задача 14. Вы уезжаете за границу на два года и сдаете свою квартиру в аренду за 50 долл. США в месяц, идущих на ваш счет авансовыми платежами под 12% годовых. Какова текущая стоимость такой аренды? Решение: 1 этап. Предмет исследования — современная стоимость потока платежей. Цель исследования — определить современную стоимость аренды квартиры. 2 этап. Структурные элементы данной экономической ситуации: ежемесячная выплата; годовая процентная ставка; срок. 3 этап. Современная (текущая) стоимость будущих платежей есть сумма текущих стоимостей месячного платежа, осуществляемого в конце каждого срока, с учетом начисленных процентов. этап. Современная стоимость первого платежа 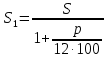 второго 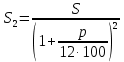 двадцать четвертого 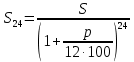 Современная стоимость рассматриваемого потока платежей является суммой современных стоимостей 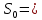 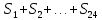 , а значит , а значит 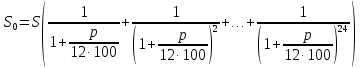 Выражение в скобках представляет собой сумму 24 членов геометрической прогрессии 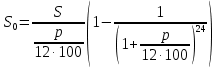 5 этап. Подставляя известные величины в построенную модель, получим: 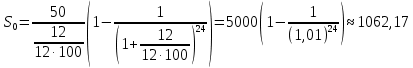 этап. Текущая стоимость такой аренды равна 1062,17 долл. США. Организация педагогического эксперимента и его результаты Экспериментальное обучение проводилось в 9 А классе МОУ «СШГ № 3», г. Каменка. В соответствии задачами исследования, нами был разработан план педагогического эксперимента. Он проводился традиционно, в три этапа. Целью констатирующего этапа было исследование использования экономико-математических задач на уроках математики в средней школе при традиционной методики преподавания, а также возможностей их использования, методических приемов, связанных сведением основных понятий, связанных с этими задачами. Во время констатирующего эксперимента педагогического эксперимента нами были использованы такие методы, как анкетирование учащихся и учителей, индивидуальная беседа, как с учителями, так и самими учащимися, наблюдение за учебной деятельностью девятиклассников и деятельностью учителей на уроках математики, наблюдение за индивидуальной учебной деятельностью учащихся при решении задач прикладного характера. Анкетирование среди учащихся показало, что им интереснее решать не абстрактные задачи, а задачи, которые связаны с реальной действительностью, задачи, в ходе решения которых появляются знания и умения, необходимые в повседневной жизни. На вопрос анкеты для учащихся «Как часто при изучении того или иного раздела математики ты понимаешь, связь этого материала с жизнью, с практикой, используешь знания, полученные на других предметах?» большинство учащихся ответило, что не задумывались об этом. При этом в своих ответах школьники указали на то, что понимание ими взаимосвязи изучаемого предмета с повседневной жизнью, повысило бы их интерес к этому предмету, активизировало бы познавательную деятельность. Также нами была предложена входная контрольная работа. Цель данной работы было получение информации об умении учащимися решать задачи прикладного характера, о знании основных этапах математического моделирования и умений осуществлять определенную деятельность на каждом этапе, в частности, умение анализировать задачу, конструировать простейшие модели реальных ситуаций, критически оценивать результаты задачи. Работа включала в себя три задачи, требующие как математических, так и определенных экономических знаний. С содержанием проверочной самостоятельной работы можно ознакомиться в Приложении № 1. Результаты входной работы приведены в таблице. Таблица 8 Результаты входной контрольной работы
Основные ошибки на этапе построения аналитических математических моделей были следствием выделять основные элементы текста условия, их взаимосвязи друг с другом. Кроме того, в ходе решения задач допускались ошибки и в процессе работы над самой математической моделью. Наряду с вычислительными ошибками, учащиеся допускали ошибки в построении математической модели, неверно упрощали полученные формулы. Также мы уделили особое внимание сформированности умения верно интерпретировать полученные результаты решения. Результаты проверочной самостоятельной работы показали, что 58 % школьников стремятся быстрее получить ответ, считая это самым главным при решении задачи. Более половины учащихся, участвующих в констатирующем эксперименте, допустили ошибки при интерпретации полученного результата, который у большинства сводился лишь к проверке вычислений, смысловая же проверка практически отсутствует. Нужно отметить, что полностью справились с заданием только 18% учащихся. Результаты констатирующего этапа эксперимента привели нас к следующим выводам: в условиях традиционной методики преподавания математики, умение решать задачи прикладного характера, и в частности, задачи с экономико-математическим содержанием, сформировано слабо или даже не сформировано вообще. Следствием этого является отсутствие интереса к решению задач и к самому предмету. Для повышения уровня сформированности умения решать задачи прикладного характера и задачи с экономико-математичеким содержанием, в частности, следует обратить особое внимание на использование школьниками последовательности этапов моделирования реальных процессов, и, как следствие, умение строить математические модели различных экономических процессов. Далее мы перешли ко второму этапу - обучающему эксперименту. Эффективность разработанной методики по отношению к качеству усвоения материала проверялась и оценивалась по результатам анализа самостоятельных и контрольных работ, которые проводились на этапах закрепления и обобщения изучаемого материала. В качестве критериев оценки эффективности было предложено: оценить объем знаний; оценить качество усвоения изученного материала. На данном этапе педагогического эксперимента перед нами стояли такие задачи, как проверка доступности содержания предлагаемого материала; проверка разработанных учебно-методические материалов на предмет формирования прикладной значимости понятий простого и сложного процента. После изучения каждой темы девятиклассникам предлагались самостоятельные работы, включающие в себя задачами финансовой математики, наиболее ярко характеризующими приложение данного математического аппарата. По окончании изучения простых процентов и простого процентного роста, с целью проверки уровня усвоения учебного материала школьниками, была предложена самостоятельная работа, рассчитанная на 20-25 минут урока. Нужно отметить, что большинство учащихся справилось с работой за более короткий промежуток времени. В заключение изучения раздела «Сложные проценты и сложный процентный рост» учащимся также была предложена вторая самостоятельная работа. Результаты решения учащимися этих двух самостоятельных работ представлены в таблице. Таблица 9 Результаты самостоятельных работ по темам «Проценты, простой процентный рост» и «Сложные проценты, сложный процентный рост»
После изучения этих тем учащимся была предложена контрольная работа, также содержащая три задачи, как и входная контрольная. Результаты контрольной работы приведены в таблице Таблица 10 Результаты итоговой контрольной работы
Оценки за контрольную работу были распределены следующим образом: 36 % учащихся написали работу на «отлично», 41 % — на «4», 17 % - на «3» и лишь 6 % - не справились с работой. Сравнительный анализ результатов решения задач с экономико-математическим содержанием до и после изучения материала по предлагаемой методике представлен на рисунке 2. 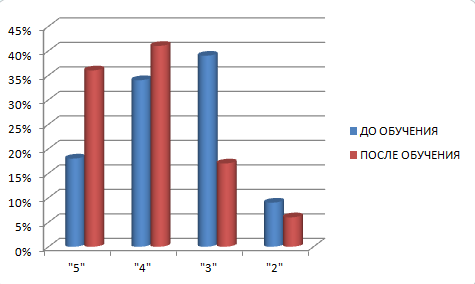 Результаты выполнения учащимися промежуточных самостоятельных работ и заключительной контрольной работы свидетельствуют о том, что большинство школьников успешно овладели полученными знаниями и смогли их применить в новых реальных ситуациях. В процессе эксперимента апробировались различные средства, формы и методы проведения занятий. Учащиеся позитивно реагировали на такое разнообразие в подаче материала, чувствовалась заинтересованность в приобретении ими знаний. Эксперимент также показал, что учащиеся стали более заинтересованно относиться и к другим прикладным задачам, не только к задачам с экономико-математическим содержанием. Таким образом, эксперимент показал реализуемость нашей гипотезы. Качественная оценка результатов педагогического эксперимента позволяет сделать вывод об эффективности разработанной методики. Апробация методики показала свою доступность и перспективность при обучении решению задач с экономико-математическим содержанием. Выводы по главе 2 Вопрос расширения прикладной направленности курса алгебры основной школы связан с решением задач с экономико-математическим содержанием. Раскрытие прикладного аспекта происходит двумя различными путями: во-первых, опираясь на математический аппарат, изучаемый в основной школе; и, во-вторых, путем введения некоторых дополнительных математических сведений в темы курса. Определены темы курса алгебры основной школы, в которые целесообразно включать задачи с экономико-математическим содержанием. Выбран математический аппарат и его место в курсе алгебры основной школы, дополняющий отдельные темы курса и позволяющий решать прикладные задачи с экономическим содержанием. Эффективность разработанной методики решения задач с экономико-математическим содержанием подтверждена проведенным педагогическим экспериментом. Заключение В ходе проведенного теоретического и экспериментального исследования получены следующие результаты. Проведенный анализ психолого-педагогической и научно-методической литературы по проблеме внедрения задач с экономическо-математическим содержанием в курс математики основной школы показал, что включение данного вида задач усиливает прикладную направленность обучения математики Выявлены особенности математических задач с экономико-математическим содержанием; проанализированы различные схемы построения математической модели их решения. Рассмотрены педагогические возможности использования компьютерных технологий обучения математике. Определено место включения рассматриваемых задач в курсе математики основной школы. Указан раздел экономики — финансовая математика, который опирается на математический аппарат, изучаемый в курсе математики основной школы. Разработана методика решения обучения решению задач с экономико-математическим содержанием, опирающаяся во-первых, на математический аппарат, изучаемый в основной школе и, во-вторых, на аппарат, дополнительно вводимый в темы курса математики основной школы. Рассмотрены задачи с экономическо-математическим содержанием, решение которых основано на аппарате сложных процентов. Проведен педагогический эксперимент по проверке эффективности методики решения задач с экономико-математическим содержанием на уроках алгебры в основной школе. Эксперимент подтвердил гипотезу исследования. Включение задач с экономико-математическим содержанием в курс математики основной школы способствует раскрытию и расширению прикладного аспекта изучаемого математического материала. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
