Экономические задачи. Диплом Кирилл. Квалификационная работа методика обучения решению экономикоматематических задач в средней школе Работу

• Название: Квалификационная работа методика обучения решению экономикоматематических задач в средней школе Работу
• Анкор: Экономические задачи
• Дата: 28.10.2021
• Размер: 154.22 Kb.
• Имя файла: Диплом Кирилл.docx
• Тип: Реферат; #258572
• страница: 3 из 5

Задача 3. Вкладчик внес на счет в банке 2700 долл. США. Банк выпла­чивает простые проценты по ставке 5,6 % годовых. Определите, какая сумма будет через 2 года 5 месяцев и 15 дней. На сколько процентов увеличится вклад?

Решение:

1 этап. Предмет исследования — функционирование денежного капитала.
Цель исследования - нахождение суммы капитала через определенный промежуток времени.

2 этап. Структурные элементы, соответствующие данной экономической ситуации:

• 
  первоначальный капитал;
  
• 
  годовая процентная ставка;
  
• 
  способ начисления — простые проценты;
  

3 этап. Наращенная сумма получается путем сложения начальной суммы и дохода, полученного от вложения денег.

4 этап. Модель, описывающая данную экономическую ситуацию, уже нам известна и выражена следующей формулой: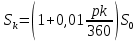



kкоторых хранится вклад.

5 этап. В нашей задаче к = 2 360 + 5 30 + 15 = 885, следовательно,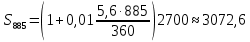


6 этап. Через заданный промежуток времени накопленная сумма соста­вит 3072,6 долл. США, при этом вклад вырастет приблизительно на 13,8%.

Существует еще целый ряд задач экономико-математического содержания, решение которых основывается на знании простых процентов. Но, кроме владения математическим аппаратом, для их решения необходимо знание определенной экономической терминологии. Учащиеся могут ее узнать из краткой справки учителя или им можно дать задание самостоятельно выяснить, что обозначают основные финансовые показатели процесса наращения, такие как процентная ставка, учетная ставка, дисконт-фактор, наращенная сумма, ставка наращения.

Процентная ставка — это цена использования денежной ссуды или капи­тала. Она определяется отношением процентных денег, уплаченных (полу­ченных) за единицу времени (обычно за год), к величине исходного капитала.

Учетная ставка - процент, взимаемый банком за предоставленный кре­дит; определяется отношением процентных денег, уплаченных (полученных) за единицу времени (обычно за год), к ожидаемой к получению (возвращае­мой) сумме денежных средств.

Дисконт-фактор — это процент, взимаемый банком.

Процесс, в котором заданы исходная сумма и ставка, в финансовых вы­числениях называется процессом наращения, искомая величина называется наращенной суммой, а ставка — ставкой наращения.

Также с использованием простых процентов решается часть задач на кредитования. Их решение основано на достаточно простом математическом аппарате, при этом они имеют прикладной характер. Кроме того они являются подготовительными для задач на кредитование при решении которых используются сложные проценты.

Задача 4. Предприниматель получил на полтора года кредит в размере 70 тыс. р. с условием возврата 90 тыс. р. Определите процентную ставку, учетную ставку и дисконт-фактор за два года. Чему равен индекс роста суммы кредита?

Решение:

1. 
   этап. Предмет исследования — процесс наращения. Цель исследования — определение основных финансовых показателей процесса наращения (про­центной ставки, учетной ставки и дисконт-фактора) за определенный про­межуток времени.
   
2. 
   этап. Структурные элементы, соответствующие данной экономической ситуации:
   

• 
  сумма кредита;
  
• 
  сумма долга;
  
• 
  процентная ставка;
  
• 
  учетная ставка;
  
• 
  индекс роста суммы кредита;
  
• 
  дисконт-фактор.
  

3 этап. Процентная ставка исчисляется как отношение суммы денег, выплачиваемых в качестве платы за пользование ссудой, к величине ссуды, а
учетная ставка есть отношение суммы денег, выплачиваемых в качестве платы за пользование ссудой, к величине возвращаемой суммы. Дисконт-фактор вычисляется как отношение суммы кредита к сумме выплаты.

4 этап. Обозначим через 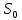- сумму ссуды, S_в— сумму возврата, r—

процентная ставка, d— учетный процент, v - дисконт-фактор.

Тогда значения данных экономических величин будут находиться по формулам : ; ;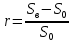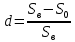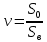

5 и 6 этапы. Проведем расчеты по перечисленным формулам, используя

данные задачи, и интерпретируем их.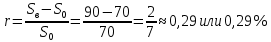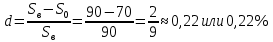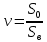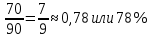

;

; ;

=

Задача 5. Предприниматель 18 апреля обратился в банк за ссудой до 19 ноября того же года под простую процентную ставку 25% годовых. Банк, удержав в момент предоставления ссуды проценты за весь ее срок, выдал предпринимателю 12 тыс. усл. д.ед. Какую сумму необходимо будет вернуть банку, если при расчете начисленных процентов использовались обыкновен­ные проценты с точным числом дней?

Решение:

1. 
   этап. Предмет исследования - процесс кредитования. Цель исследования - определение суммы возврата.
   
2. 
   этап. Элементы, участвующие в тексте условия данной задачи:
   

• 
  сумма кредита;
  
• 
  сумма процентных выплат;
  
• 
  процентная ставка;
  
• 
  количество дней, на которые берется кредит.
  

3 этап. Сумма процентных выплат это отношение суммы выданных денег к разности 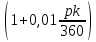, выражающей уменьшенный процентный рост на проценты, начисленные за время кредита.

4 этап. Обозначим через Sсумму, которую необходимо вернуть банку, через к - количество дней, на которые взят кредит, р — процентную ставку, S— выплаченные проценты, то: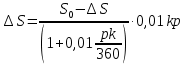

5этап.k=215,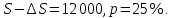

Значит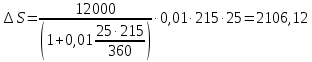
А так как S = S₀ + S, то S = 12000 + 2106,12 = 14106,12.

6 этап.19ноября предприниматель обязан будет вернуть банку14106,12 усл. д.ед.

Для проверки найдем простые проценты, начисленные за 215 дней на

сумму 14106,12 усл. д.ед. по ставке 25% годовых по формуле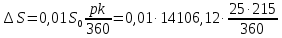

=2106,12, что подтверждает правильность вычислений.

Задача 6. Покупатель приобрел телевизор стоимостью 12,8 тыс. р. При этом он сразу уплатил 25% стоимости телевизора, а на остальную сумму получил кредит на 6 месяцев под простую процентную ставку 10% годовых. Кредит погашается ежемесячными платежами. Составьте план погашения кредита.

Решение:

1. 
   этап. Предмет исследования - погашение кредита. Цель исследования — составление плана погашения.
   
2. 
   этап. Структурные элементы, описывающие данную экономическую ситуацию:
   

• 
  первоначальная стоимость;
  
• 
  ежемесячный погасительный платеж;
  
• 
  срок погашения;
  
• 
  простая процентная ставка на остаток.
  

3 этап. При данном способе погашения кредита учитывается, что долг
не является постоянной величиной, а с течением времени уменьшается, процентные платежи за пользование потребительским кредитом рассчитыва­ются каждый раз на оставшуюся часть долга. Сам же долг рассчитывается равными суммами. Ежемесячные погасительные платежи представляют собой сумму выплаты части основного долга и процентного платежа данного меся­ца.

4 этап. Поскольку покупатель сразу уплатил 12,8 0,25 =3,2 тыс. р., то

он получил кредит 12,8-3,2 = 9,6 тыс. р. Каждый месяц выплачивается часть основного долга размером 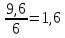тыс.р. Процентные платежи R для каждого месяца находятся с учетом постепенного уменьшения величины долга по формуле: 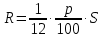, где S- сумма текущего долга, ар—годовая процентная ставка.

5 и 6 этапы. Найдем по выведенной формуле процентные платежи первого и последующих месяцев. За первый месяц начисляются проценты в размере: 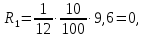08

За второй месяц начисляются проценты на остаток долга: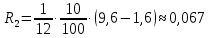



Аналогичным образом для третьего платежа получим: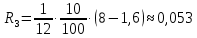

и т.д. Таким образом, R₄=0,04, R_s=0,027, и R₆=0,013. Следовательно,

общая величина процентного платежа (стоимость кредита):

R= 0,08 + 0,067 + 0,053 + 0,04 + 0,027 + 0,013 = 0,28.

Для наглядности представим план погашения кредита в табличном виде (таблица № 4).

Таблица № 4

План погашения кредита

Номер месяца	Остаток основно­го долга на нача­ло месяца	Процентный платеж	Ежемесячная выплата основ­ного долга	Величина ежемесячного погаситель­ного платежа
1	9600	80	1600	1680
2	8000	67	1600	1667
3	6400	53	1600	1653
4	4800	40	1600	1640
5	3200	27	1600	1627
6	1600	13	1600	1613
		280	9600	9880