все лабы. Все лабы. Лабораторная работа 1 1 Цель работы
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
и само число 38.15 ( 10 ) 100110.0010 ( 2 ) . Примечание – процесс перевода правильной дроби (или дробной части числа) нужно продолжать до тех пор, пока промежуточные дробные части не обратятся в нуль (как это имело место в первом примере), или не обнаружится период, или пока не будет достигнута желаемая точность (во втором примере перевод сделан с точностью до четвертого знака после точки). Тот же результат получается и при использовании (6.4): 38.15 ( 10 ) =11(1010)1+ 1000(1010)0+ 1(1010)-1+ 101(1010)-2 100110.0010 ( 2 ). 6.2.10 Пример 3. Перевести из десятичной системы счисления в шестнадцатеричную число 396.05 (10). В данном случае десятичная система является исходной, а шестнадцатеричная - новой, при этом основание новой системы в исходной q16 = 16 (10) .
и само число 396.05 ( 10 ) 18С.0СС ( 16 ) . Чтобы воспользоваться для перевода (6.4), нужно знать правила арифметических действий над шестнадцатеричными числами, поэтому такой вариант перевода не рекомендуется применять. 6.2.11 Пример 4. Перевести из шестнадцатеричной системы счисления в десятичную число F9E.A8 ( 16 ) . В данном случае шестнадцатеричная система является исходной, а десятичная - новой, при этом основание новой системы (q10 = 10) в исходной системе 10 ( 10 ) = А ( 16 ). В рассматриваемом примере, в отличие от предыдущего, проще выполнить перевод с использованием полинома (6.4). Тогда получается F9E.A8 ( 16 ) = 15 16 2 + 9 16 1 + 14 16 0 + 10 16 –1 + 8 16 –2 = = 3998.65625 ( 10 ); 6.2.12 Пример 5. Перевести шестнадцатеричное число в двоичное и наоборот. Для этого существуют простые правила, отличающиеся от рассмотренных ранее. При переводе шестнадцатеричного числа в двоичное достаточно заменить каждую цифру этого числа соответствующим четырехразрядным двоичным числом, отбрасывая ненужные нули в старших разрядах целой части и в младших разрядах дробной части:      1010 1110 0011 0000 1111 1010 1110 0011 0000 1111 АЕ3.0F ( 16 ) = А Е 3 0 F ( 16 ) = = 101011100011.00001111 ( 2 );     1D.9C ( 16 ) = 1 D 9 C ( 16 ) = 11101.100111 ( 2 ) . 1D.9C ( 16 ) = 1 D 9 C ( 16 ) = 11101.100111 ( 2 ) . 0001 1101 1001 1100 При переводе двоичного числа в шестнадцатеричное поступают следующим образом: двигаясь от точки влево и вправо разбивают двоичное число на группы по четыре разряда (тетрады), дополняя при необходимости нулями крайние левую и правую тетрады. Затем каждую тетраду заменяют шестнадцатеричной цифрой: 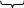 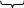 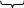 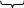 100110.0010011 ( 2 ) = 0010 0110 0010 0110 ( 2 ) = 26.26 ( 16 ); 100110.0010011 ( 2 ) = 0010 0110 0010 0110 ( 2 ) = 26.26 ( 16 );2 6 2 6 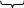 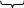 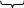 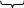 11101.01101 ( 2 ) = 0001 1101 0110 1000 ( 2 ) = 1D.68 (16 ) . 11101.01101 ( 2 ) = 0001 1101 0110 1000 ( 2 ) = 1D.68 (16 ) .1 D 6 8 Примечание – любое число х можно перевести из шестнадцатеричной системы счисления в десятичную и обратно, применив промежуточное преобразование:  Х ( 16 ) х ( 2 )х ( 10 ) или х ( 10 ) х ( 2 ) х ( 16 ) . Х ( 16 ) х ( 2 )х ( 10 ) или х ( 10 ) х ( 2 ) х ( 16 ) .6.2.13 Одно из применений шестнадцатеричной системы счисления в вычислительной технике - это индикация адресов ячеек внутренней памяти, куда входят оперативное запоминающее устройство (ОЗУ) и постоянное запоминающее устройство (ПЗУ). Каждая из М ячеек, обладающая емкостью N бит - двоичных разрядов, имеет свой адрес. Адреса начинаются с 0 и заканчиваются (М-1). Например, адрес первой ячейки 000000 h , второй – 000001 h и т.д., где латинская буква “h“ указывает на принадлежность числа шестнадцатеричной системе счисления (hex). 6.2.14 Двоичная арифметика. Правила выполнения арифметических операций над числами для позиционной системы счисления с любым основанием S задаются таблицами сложения, вычитания и умножения одноразрядных чисел. Ниже представлены таблицы 6.1 – 6.3 для двоичной арифметики.
Сложение двух единиц в любом разряде числа даёт единицу переноса в следующий, старший разряд. При займе единицы из следующего старшего разряда она даёт две единицы в текущем разряде. Умножение многоразрядных чисел производится путём образования частичных произведений и последующего их суммирования. 6.2.15 Пример 6. Вычислить в двоичной системе счисления x= (a+ b* c) / (d– e), где a = 10010111,001 ( 2 ); b = 1011,11 ( 2 ); c = 110 ( 2 ); d = 100010 ( 2 ); e = 11101,1 ( 2 ). Решение: а) d – e = 100,1;
б) b * c = 1000110,10;
в) a + b * c = 11011101,101;
г) x = (a + b * c) / (d – e) = 110001,01.
Приведённый пример показывает, что двоичная система очень удобна для вычислений. Операция умножения сводится к простому сложению со сдвигом множимого по позиции. Операция деления сводится к вычитанию со сдвигом делителя. 6.2.16 Рассмотрим формы представления чисел в позиционной системе счисления. Существует две формы записи чисел: форма FIXED – с фиксированной точкой (запятой) и FLOAT – с плавающей точкой (запятой). Форма FIXED характеризуется тем, что местоположение точки фиксируется либо перед старшим разрядом, либо после младшего разряда числа. В ряде ЭВМ первых поколений преимущественно применялась данная форма. В принципе, все вычисления над числами можно выполнить, представив их в форме FLOAT. Но есть задачи, где выгоднее использовать форму FIXED. В современных ЭВМ она применяется для записи целых чисел, при этом точка фиксируется после младшего разряда. В этом случае быстродействие процессора увеличивается. Форма FLOAT происходит от так называемой полулогарифмической формы для записи макро – и микровеличин. Например, скорость света С = 3*10 5 км /с; масса одного атома водорода m = 1,66*10 –24 г. В общем виде форма FLOAT записывается х = m q P, (6.6) где q – основание системы счисления; m – мантиса числа; р – порядок. В вычислительной технике применяется нормализованный вид FLOAT. При использовании этого вида нужно соблюдать условие: q – 1 m < 1, (6.7) (мантиса меньше единицы и первая цифра дробной части – значащая, то есть отличная от нуля). Например, числа 128,36 и 0,0078 будут представлены в нормализованном виде FLOAT: 0,12836 10 3 и 0,78 10 –2. Правила выполнения арифметических операций над числами, представленными в форме FLOAT, формулируются следующим образом: а) сложение: пусть требуется вычислить z = x + y , где x = m X 10 Px ; y = m Y 10 Py ; для этого: – выравниваются порядки чисел по p MAX = max ( p X , p Y) за счёт перемещения мантисы (сдвига) относительно запятой; – алгебраически складываются мантисы; – результат нормализуется, приводится к виду (6.7), при этом может возникнуть порядок нормализации; – порядок результата p Z = p MAX + p НОРМАЛИЗАЦИИ . б) вычитание: вычитание сводится к алгебраическому сложению уменьшаемого с вычитаемым, взятым с обратным знаком, поэтому не требует специального объяснения; в) умножение: нужно перемножить мантисы, нормализовать их произведение, а порядок будет p Z = p X + p Y + p НОРМАЛИЗАЦИИ ; г) деление: z = x / y = (m X q Px) / (m Y q Py ) = (m X / m Y) q Px – Py = = m Z q Pz и, если нужно, нормализовать m Z. 6.2.17 Пример 7. Вычислить z = x + y, где x = 0,512310 2, y = 0,86 10 2. Если порядки равны, то выравнивание не производится. m Z = m X + m Y = 0,5123 + 0,86 = 1,3723 , получили ненормализованную мантису. Нормализуем её и получим m Z = 0 , 13723 10 1 , где p НОРМАЛИЗАЦИИ = + 1 , тогда p Z = p MAX + p НОРМАЛИЗАЦИИ = 2 + 1 = 3 , и в итоге имеем z = x + y = m Z 10 Pz = 0 , 13723 10 3 . 6.2.18 Пример 8. Вычислить z = x + y, где x = 0 , 2567 10 2 , y = 0 , 26 10 –1. Выравниваем порядки: p MAX = p X = 2 , тогда x = 0 , 2567 10 2 , y = 0 , 00026 10 2 ; m Z = m X + m Y = 0 , 2567 + 0 , 00026 = 0 , 25696 (мантиса получилась в нормализованном виде). В итоге z = x + y = m Z 10 Pz = 0 , 25696 10 2 . 6.2.19 Обратный и дополнительный коды. При выполнении привычных алгебраических операций используются числа со знаком « + » и « – ». В устройствах ЭВМ коды чисел представляются в специальной беззнаковой форме. С этой целью введены обратный и дополнительный коды чисел. Тогда операция вычитания заменяется операцией сложения прямого кода уменьшаемого и дополнительного кода вычитаемого. Код числа со знаком вида (6.5) называется прямым кодом. В таком виде числа представляются в привычном для нас виде. Если система счисления двоичная, то для знака достаточно выделить один дополнительный двоичный разряд. Знак может принимать одно из двух значений: « + » обозначается 0 и « – » обозначается 1. Пусть имеется некоторое устройство (регистр, ячейка памяти ЭВМ), содержащее k разрядов в системе счисления q . Первый слева (старший) разряд хранит признак знака числа. В частности, если в нём 0 , то число положительное и в устройстве хранится прямой код числа. В качестве признака отрицательного числа используется старшая цифра базиса системы счисления (для q = 2 это 1; для q = 10 это 9 ; для q = 16 это F). В остальных разрядах устройства для отрицательного числа записываются цифры базиса, обратные цифрам прямого кода – так называемый обратный код числа. Две цифры базиса называются взаимно – обратными, если их сумма составляет старшую цифру базиса. Иногда употребляют понятие «обратный базис». Например, для базиса q = 10 (0 , 1 . 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9) обратным базисом будет 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 , и обратный код числа х = – 28,356 ( 10 ) в 10 – разрядном устройстве с запятой перед третьим разрядом (форма FIXED) будет представлен так:
 Признак знака числа (в данном случае отрицательного) [обр] Правило: чтобы получить из прямого кода отрицательного числа обратный код, нужно взять (k – 1) – разрядный прямой код числа без знака (то есть модуль числа), дополнив старшие разряды нулями (если потребуется) и заменить цифры в разрядах обратными. В этом же устройстве прямой код числа х1 = + 28,356 ( 10 ) будет представлен так:
 Признак знака числа (в данном случае положительного) [прямой] Если выполним действие х + х1 , то получим нуль: – 28,356 ( 10 ) + + 28,356 ( 10 ) = 0, а если сложим два кода этих же чисел, то во всех разрядах получим девятки:
то есть обратный код нуля. А это неудобно, поэтому был введён дополнительный код. Он позволяет представлять нуль всегда в прямом коде. Если к обратному коду прибавить единицу в младший разряд, то получится дополнительный код числа. Можно получить дополнительный код числа, минуя перевод его в обратный код, для чего следует руководствоваться следующим правилом. Правило: для получения дополнительного кода отрицательного числа нужно представить его модуль в устройстве и вычесть прямой код из единицы следующего старшего, по устройству, разряда (то есть (k + 1) – го разряда). Дополнительный код числа х = – 28,356 ( 10 ) в 10 – разрядном устройстве будет представлен так:
 Признак знака числа (в данном случае отрицательного) [доп] и теперь сложение его с прямым кодом числа х1 = + 28,356 ( 10 ) даёт чистый нуль:
при этом появляется единица переноса в несуществующий следующий старший разряд. Поскольку этого разряда в устройстве нет, то единица теряется, а в устройстве записывается правильный результат, то есть + 0. Подчеркнём дополнительно такие обстоятельства: а) использование дополнительного кода для изменения знака числа позволяет ограничиться технической реализацией только одной операции сложения (не требуется реализовывать техническую операцию вычитания), при этом вычитание просто сводится к сложению уменьшаемого с дополнительным кодом вычитаемого; б) если результат получается в прямом коде, то разность положительная, а в дополнительном коде, то разность отрицательная; в) перевод из обратного или дополнительного кода производится по рассмотренным выше правилам. 1.2.20 Пример 9. Вычислить в q = 10 y = x – x1, где x = + 13,13; x1 = = – 26,26. Решение: а) применив стандартные правила алгебры, получим y = x – x1 = + 13,13 – 26,26 = – 13,13; б) с применением дополнительного кода для 10 – разрядного устройства получим
а девятка в крайнем левом разряде указывает на то, что получен дополнительный код, следовательно, число y отрицательное; в) модуль числа y вычисляется
и окончательный результат: y = – 13,13. 6.2.21 Получение дополнительного кода отрицательных двоичных чисел осуществляется по тем же правилам. Пусть в качестве устройства, куда записываются коды, используется 32 – разрядный регистр, у которого первый слева разряд предназначен для хранения признака кода. Например, число – 38 (10 ) = = – 100110 ( 2 ) в регистре может быть представлено так:
[доп]
 Номер разряда Очень просто получается обратный двоичный код инвертированием каждого разряда (заменой 0 на 1 и 1 на 0). Для получения дополнительного кода достаточно прибавить к младшему разряду единицу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
