все лабы. Все лабы. Лабораторная работа 1 1 Цель работы
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
1 ИССЛЕДОВАНИЕ СПОСОБОВ ЛОГИЧЕСКОЙ МИНИМИЗАЦИИ ФУНКЦИЙ. ЛАБОРАТОРНАЯ РАБОТА № 11.1 Цель работы Целью работы является овладение практическими навыками преобразования логических функций до минимального вида, удобного для практической реализации устройств, которые описываются этими функциями. 1.2 Теоретические сведения 1.2.1 Под минимизацией понимается упрощение и преобразование логических функций до вида, приемлемого для их аппаратной реализации и создания простого по составу и эксплуатации узла или модуля вычислительного устройства. Существует два способа минимизации: аналитический и графический. 1.2.2 Аналитическая минимизация требует определенной интуиции проектировщика и применима для простых функций небольшого числа аргументов. Для сложных функций разработаны машинные алгоритмы. Можно рекомендовать теорему Квайна. Перед минимизацией по Квайну логическая функция должна быть развернута, если она задана в произвольной форме. Это означает, что она должна содержать все наборы, каждый из которых включает все логические переменные (с инверсией и без нее) и нет одинаковых наборов. Чтобы достичь этого, можно, например, умножить набор, не содержащий какого-либо аргумента, на логическую единицу (в частном случае x+ 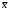 =1) и получить взамен одного два набора. В представленной в таком виде функции следует провести сначала все возможные операции склеивания и затем все возможные операции поглощения (смотри лабораторные работы дисциплины "Физические основы ЭВМ"), в результате получится сокращенная функция. В принципе, при аналитической минимизации можно использовать все соотношения алгебры логики. =1) и получить взамен одного два набора. В представленной в таком виде функции следует провести сначала все возможные операции склеивания и затем все возможные операции поглощения (смотри лабораторные работы дисциплины "Физические основы ЭВМ"), в результате получится сокращенная функция. В принципе, при аналитической минимизации можно использовать все соотношения алгебры логики.1.2.3 Для поиска лишних наборов используют метод испытаний: чтобы испытать некоторый набор функции, следует исключить его и подставить в оставшееся выражение такие значения аргументов, которые обращают исключенный набор в единицу (если функция составлена по истинным значениям наборов). Если при такой подстановке оставшееся выражение окажется тождественно равным единице, то испытываемый набор является лишним. Рассмотрим пример. Пусть задана логическая функция F = A C + 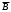 C + C +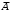 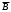 . .Испытаем набор AC, обращаемый в 1 при A = C = 1. Подставив в оставшееся выражение F = 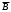 C + C + 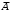 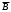 значения A = C = 1, получим F = значения A = C = 1, получим F = 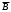 1+0 1+0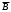 . При B = 0 последнее выражение равно 1, но при B= 1 оно равно 0. Следовательно, набор AC не является лишним и его исключить нельзя. Испытаем набор . При B = 0 последнее выражение равно 1, но при B= 1 оно равно 0. Следовательно, набор AC не является лишним и его исключить нельзя. Испытаем набор 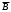 C, обращаемый в 1 при B = 0, C = 1. Подставив в оставшееся выражение F= AC + C, обращаемый в 1 при B = 0, C = 1. Подставив в оставшееся выражение F= AC +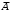 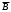 значения B = 0, C = 1, получим F = A1 + значения B = 0, C = 1, получим F = A1 + 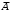 1. Последнее выражение равно 1 как при A = 1, так и при A = 0. Значит набор 1. Последнее выражение равно 1 как при A = 1, так и при A = 0. Значит набор 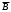 C можно опустить, и окончательно функция запишется F = AC + C можно опустить, и окончательно функция запишется F = AC +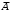 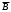 . .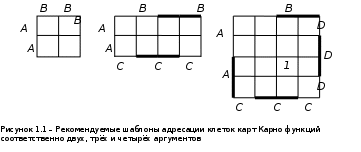 1.2.4 Графическая минимизация основана на применении карт Карно. Карта Карно - это прямоугольник, разбитый на клетки, число которых равно максимальному числу наборов функции, т.е. 2n, где n - число аргументов. Каждая клетка соответствует одному набору и туда записывается его значение: 1 или 0. В случае недоопределенной функции клетка может быть заполнена, например, символом (-) для неизвестного набора или символом () - для запрещенного набора. Каждая клетка имеет свой адрес. Ниже на рисунке 1.1 даны рекомендуемые шаблоны адресации клеток карт Карно двух (A,B), трёх (A,B,C) и четырёх (A,B,C,D) аргументов. После заполнения клеток значениями наборов (например, набору ABCD=1 принадлежит клетка правой карты рисунка 1.1, куда проставлена 1) выполняется минимизация функции. Отыскание минимальной ее формы сводится к объединению соседних клеток, при этом соседними считаются и все крайние клетки с учетом «цилиндричности» карты относительно вертикальной и горизонтальной осей. Можно сформулировать ряд общих правил: а) минимизировать можно как по единичным, так и по нулевым значениям наборов в зависимости от состава функции; б) объединять клетки можно по столбцам, по строкам, по квадратам (учитывая и «цилиндричность» карты); в) число клеток, объединяемых в одну группу, должно быть или 2, или 4, или 8, или 16 и никаким другим (для функций с количеством аргументов не более четырёх); г) количество групп объединяемых клеток может быть любым; д) нужно стремиться объединять в каждую группу как можно большее число клеток и сводить к минимуму количество групп объединяемых клеток. С этой целью полезным будет пункт (е) правил; е) в случае недоопределенной функции ее можно доопределить, проставив в клетки неизвестных или запрещенных наборов 1 или 0, если это необходимо для выполнения пункта (д) правил; ж) одна или несколько клеток могут входить в более чем одну группу объединяемых клеток. После объединения клеток можно записать минимальную форму функции, у которой количество наборов равно количеству групп объединенных клеток, т.е. каждый набор соответствует «своей» группе клеток. При этом каждый набор содержит те аргументы, которые являются общими для группы, т.е. не меняют своего значения (например, с 1 на 0 или наоборот).  Например, недоопределенная функция трёх аргументов содержит наборы, размещенные в клетках карты Карно на рисунке 1.2: один набор 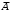 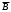 C является неизвестным, а другой набор ABC - запрещенным. Если не прибегать к доопределению функции, то количество групп объединенных клеток равно трем, и минимальная форма функции может быть записана в виде C является неизвестным, а другой набор ABC - запрещенным. Если не прибегать к доопределению функции, то количество групп объединенных клеток равно трем, и минимальная форма функции может быть записана в виде F= 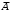 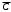 + + 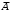 B + B B + B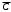 . .Если доопределить функцию (рисунок 1.3), то количество групп объединенных клеток будет равно двум, и минимальная форма функции может быть записана в виде F = 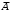 + B. + B.1.2.5 Если устройство имеет n входов и s выходов, то оно описывается s логическими функциями, каждая из которых может быть функцией n аргументов. Можно минимизировать каждую функцию в отдельности и по ним реализовать схему, которая будет состоять из s отдельных схем, имеющих одни и те же входы. Однако такой путь часто приводит к избыточности элементов в устройстве. Поэтому целесообразно рассматривать все s функций в совокупности. Это значит, что нужно стремиться выделить в них общие наборы или группы наборов, которые могут быть реализованы одним общим узлом. В случае использования карт Карно нужно выделять одинаковые группы клеток. При таком подходе некоторые функции могут оказаться не в минимальной форме, но с этим мирятся ради упрощения устройства. 1.3 Формулировка задания 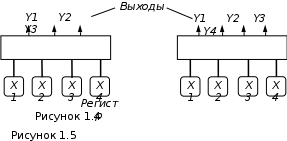 1.3.1 Задание 1. Спроектировать клавишный пульт (смотри рисунок 1.4), работающий по такому алгоритму: выходной трехэлементный код формируется с помощью нажатия одной из основных клавиш X1, X2, X3. Смена кода каждой из основных клавиш осуществляется с помощью клавиши X4 - РЕГИСТР, причем нажатому состоянию клавиши соответствует 1, отжатому - 0. Кодировка приведена в таблице 1.1. |
