все лабы. Все лабы. Лабораторная работа 1 1 Цель работы
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
2.2.3 Пусть минимальная функция представлена в виде суммы наборовF = AB + BC + AC. (2.1) Возьмем двойное отрицание и применим теорему де Моргана  F = F = AB + BC + AC = (AB)(BC)(AC),    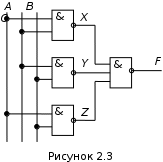 обозначим: (AB) = X; (BC) = Y; (AC) = Z. В преобразованной функции каждая пара входных переменных, заключенных в скобки с общим отрицанием, реализуется одним элементом И-НЕ с двумя входами. Получаемые на выходе каждого элемента промежуточные переменные также объединяются по закону И-НЕ. В результате схема устройства будет иметь вид рисунка 2.3. Как видно, для реализации устройства, описываемого функцией (2.1), достаточно применить элементы базиса И-НЕ. Пусть минимальная функция представлена в виде произведения наборов F = (A+B)(B+C)(A+C). (2.2) После преобразования, аналогичного предыдущему, получим  F = (A+B) + (B+C) + (A+C),    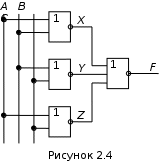 обозначим (А+В) =X; (В+С) = Y; (А+С) = Z. Каждая пара входных переменных, представленная суммой с общим отрицанием, реализуется одним элементом ИЛИ-НЕ с двумя входами, промежуточные переменные также объединяются по закону ИЛИ-НЕ. В результате схема устройства, описываемого логической функцией (2.2), будет иметь вид рисунка 2.4 и содержать элементы только одного базиса ИЛИ-НЕ. В рассмотренных выше примерах не учитывались ограничения на число входов элементов. С учетом такого ограничения (например, число входов у применяемых элементов равно двум) схемы рисунков 2.3 и 2.4 выглядели бы несколько по иному. Следует также учесть, что для сокращения числа входов элемента их можно объединять между собой. В заключении отметим без доказательства, что каждая из функций И-НЕ и ИЛИ-НЕ представляет функционально полный базис, т.е. позволяет реализовать любую булеву функцию и, следовательно, устройство, в том числе применяемое в ЭВМ. 2.3 Формулировка задания В лабораторной работе осуществляется синтез комбинационных схем, у которых выходные сигналы зависят только от значений входных сигналов в данный момент времени и не зависят от предыдущего состояния устройства (или предыстории). 2.3.1 Задание 1. Реализовать в базисе И-НЕ клавишный пульт, минимальная функция которого получена в заданиях 1 и 2 лабораторной работы № 1. Ограничения на число входов элементов отсутствуют. 2.3.2 Задание 2. Реализовать в базисе ИЛИ-НЕ клавишный пульт, минимальная функция которого получена в заданиях 1 и 2 лабораторной работы № 1. Ограничения на число входов элементов отсутствуют. 2.3.3 Задание 3. Построить мажоритарную ячейку (ячейку голосования) на три входа, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно 1, т.е. сигнал на выходе ячейки должен быть равен 1, когда на двух или трех входах присутствует сигнал, равный 1, в противном случае выходной сигнал должен быть равен нулю. Устройство реализовать в базисе:
2.4 Порядок выполнения работы 2.4.1 Выполняется при подготовке к работе: – изучить теоретические сведения; – сделать заготовку отчета, куда поместить минимальные функции устройств, рассмотренных в лабораторной работе № 1. 2.4.2 Выполняется в лаборатории: – получить задание у преподавателя. В зависимости от запланированного объема часов на данную работу для выполнения могут быть предусмотрены любые комбинации заданий, сформулированных в подразделе 2.3. Задания могут быть как индивидуальными, так и на бригаду в целом; – построить схемы комбинационных устройств. Если выдано задание 3, то осуществить полный синтез схемы в соответствии с изученными ранее правилами; – оформить отчет. Если согласно заданию проводился синтез одного и того же устройства на основе разных подходов (были взяты разные логические функции или оба элементных базиса и т.д.), то сравните полученные схемы и сделайте выводы. 2.5 Методические указания по выполнению работы 2.5.1 Перед технической реализацией логическая функция устройства должна быть подготовлена. Если минимизация проводилась с помощью карты Карно, то полученная минимальная функция уже является подготовленной, и достаточно применить теорему де Моргана, чтобы привести ее к окончательному виду (смотри теоретические сведения к данной лабораторной работе). Если функция минимизировалась аналитическим способом, то для подготовки ее к технической реализации дать однозначных рекомендаций невозможно. Например, после проведенных преобразований была получена функция вида F = A(B+C) + 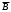 (A+C). (2.3) (A+C). (2.3)Можно предложить следующие варианты ее подготовки: а) вариант 1. К обоим скобкам применим теорему де Моргана:  (В+С) =   ; (A+C) = ; (A+C) = 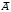 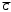 , ,в результате чего функция примет вид 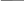 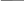 F = A F = A 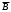 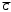 + + 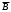 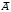 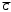 , ,и после вторичного применения теоремы де Моргана к функции в целом получим ее форму, пригодную для реализации в базисе И-НЕ; б) вариант 2. Раскроем скобки в правой части функции (2.3) F = AB + AC + A 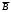 + + 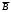 C, (2.4) C, (2.4)что сразу же дает желаемый результат, так как, применив теорему де Моргана к данной функции, получим ее форму, пригодную для реализации в базисе И-НЕ; в) вариант 3. Если в функции (2.4) испытать набор AС, то окажется, что он является лишним (это предлагается доказать студентам самостоятельно), в результате чего получим F = A + 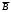 C. C.2.5.2 Ниже на примере показано, как реализовать схему устройства с несколькими выходами, если в описывающих его логических функциях есть общие члены. Пусть устройство имеет четыре входа, два выхода и соответствующие им две минимальные функции F1 = C D + 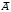 B B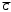 + ABC; F2 = A + ABC; F2 = A 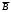 + +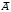 B B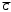 + ABC. + ABC.Применим к обоим функциям теорему де Моргана и получим  F1 = C D 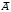 B B 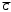 ABC; F2 = A ABC; F2 = A 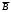 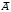 B B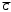 ABC. ABC.Схема устройства, реализованная на элементах базиса И-НЕ, имеет вид рисунка 2.5. 3 ИЗУЧЕНИЕ ВАРИАНТОВ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ ТРИГГЕРОВ. ЛАБОРАТОРНАЯ РАБОТА № 3 3.1 Цель работы Целью работы является закрепление теоретических знаний и приобретение практических навыков по применению триггеров в совокупности с другими логическими элементами для создания устройств. 3.2 Теоретические сведения 3.2.1 Триггеры (Тг) являются функциональными элементами, способными сохранять двоичную информацию (состояние 1 и 0) после окончания действия входных сигналов. Один Тг служит для хранения одного бита информации. При считывании информация сохраняется, а в случае отключения питания - теряется. Тг имеет один основной выход Q и дополнительный - инверсный основному или 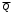 . Число входов Тг зависит от его типа. . Число входов Тг зависит от его типа.Триггеры применяются в качестве переключающих элементов; элементарных ячеек при создании счетчиков импульсов и оперативных запоминающих устройств (регистров и ОЗУ – статических запоминающих устройств); элементов временной задержки импульсов и т.д. На их долю приходится ориентировочно 20% - 40% от всех элементов средств вычислительной техники. Везде используется их основное свойство - сохранять состояние до прихода входных сигналов, в качестве которых выступают управляющие, синхронизирующие, информационные сигналы. Все многообразие прикладных задач по созданию логических устройств и узлов решается с помощью ограниченного числа типов триггеров. Перечислим основные типы триггеров, их отличительные характеристики и упрощенные условные обозначения.  3.2.2 Тг с двумя установочными входами – RS - триггер (SET – установка; RESET – сброс), асинхронный (несинхронизируемый). Тг устанавливается в единичное состояние (Q = 1) при подаче на установочный вход единицы (S = = 1). Сброс единицы на выходе Q осуществляется подачей единицы на вход сброс (R = 1). Данный тип триггера служит основой триггеров других типов; его синхронизируемый вариант используется для хранения промежуточной информации; он является неотъемлемой частью контактных клавишных устройств, т.к. обеспечивает ликвидацию явления "дребезга контактов".  3.2.3 Асинхронный (несинхронизируемый) Т - триггер со счетным входом, срабатывающий от положительного перепада входного импульса. Он служит для деления частоты входного сигнала на два. Триггер меняет свое состояние на противоположное с приходом каждого очередного входного импульса. Основная область применения - счетчики импульсов. Соединяя Т - триггеры последовательно, можно создать счетчик, который делит частоту входного сигнала на 4,8,16 и т.д. 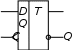 3.2.4 Синхронизируемый по входу C отрицательным перепадом синхроимпульса триггер задержки – D - триггер (delay – задержка). Он обеспечивает задержку во времени входного импульса на один - два такта последовательности синхронизирующих импульсов. Например, у однотактного D - триггера состояние логической 1 сохраняется после снятия входного сигнала до прихода очередного синхроимпульса. Данный тип триггеров широко применяется при построении регистров. 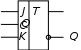 3.2.5 Универсальный синхронизируемый JK - триггер. Коммутируя внешние выводы этого Тг, можно получить аналог любого из трех рассмотренных выше типов триггеров, обладающий соответствующими качествами. В частности, подача на вход J сигнала S, а на вход K - сигнала R превращает JK -триггер в RS - триггер, только следует помнить, что набор R = S =1 является запрещенным. Если объединить входы J и K и подавать на них сигнал Т, то получится Т - триггер. Если собрать изображенную внизу схему, то получится D - триггер. 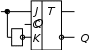 3.3 Формулировка задания 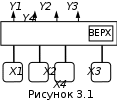 Спроектировать клавишный пульт (смотри рисунок 3.1), имеющий три символьные клавиши X1, X2, X3 и одну регистровую Х4 - переключатель регистров регистр, которая обеспечивает переход с верхнего регистра на нижний и наоборот при кратковременном нажатии. Предусмотреть индикацию смены регистра, например с помощью светового индикатора верх. На выходе пульта Y1,Y2,Y3,Y4 формируется 4-х элементный код в соответствии с таблицей кодировки (таблица 3.1). Минимизацию функций, описывающих проектируемое устройство, осуществить: – условие 1: по истинным значениям наборов; – условие 2: по ложным значениям наборов. |
