все лабы. Все лабы. Лабораторная работа 1 1 Цель работы

• Название: Лабораторная работа 1 1 Цель работы
• Анкор: все лабы
• Дата: 28.12.2021
• Размер: 0.74 Mb.
• Имя файла: Все лабы.docx
• Тип: Лабораторная работа; #320584
• страница: 4 из 13

Таблица 3.1 – Комбинации выходного кода

Регистр	Xi	Y1	Y2	Y3	Y4	Регистр	Xi	Y1	Y2	Y3	Y4
нижний	–	0	0	0	0	верхний	–	1	1	1	1
	X1	1	0	0	1		X1	1	1	1	0
	X2	1	1	0	0		X2	1	0	1	1
	X3	0	0	1	1		X3	0	1	1	1

В таблице 3.2 приведены задания, которые определяют различные подходы к проектированию одного и того же устройства. Например, задания 5 и 6 позволяют осуществить вариантное конструирование на этапе технической реализации; задания 7 и 8 - на этапе оптимизации логической модели; а задание 9 - на обоих перечисленных этапах.
Таблица 3.2 – Варианты заданий

№ задания		1	2	3	4	5	6	7	8	9
Условие		1	1	2	2	1	2	1,2	1,2	1,2
Базис	И-НЕ	+	–	+	–	+	+	+	–	+
	ИЛИ-НЕ	–	+	–	+	+	+	–	+	+

3.4 Порядок выполнения работы
3.4.1 Выполняется при подготовке к работе:

– изучить теоретические сведения подраздела 3.2 и соответствующий раздел лекционного курса;

– сделать заготовку отчета по работе, где поместить рисунок 3.1 и таблицу 3.1.
3.4.2 Выполняется в лаборатории:

– получить от преподавателя номер задания из таблицы 3.2. Для выполнения многовариантных заданий, таких, как 5-9, требуется более одного лабораторного занятия;

– выполнить поэтапный синтез устройства, начиная с составления таблицы состояний и заканчивая функциональной схемой;

– в случае многовариантного задания сделать сравнение вариантов решения между собой;

– оформить отчет.
3.5 Методические указания по выполнению работы
3.5.1 С понятием триггера, типами триггеров, особенностями их функционирования и логического синтеза можно ознакомиться в ПРИЛОЖЕНИИ Б.
3.5.2 Для фиксации регистра, выбираемого кратковременным нажатием клавиши регистр, включить в схему устройства триггер, вход которого связан с данной клавишей, при этом указать тип применяемого триггера.
3.5.3 Начать логический синтез нужно с составления таблицы истинности, где должен учитываться выходной сигнал триггера в качестве одной логической переменной.
3.5.4 Минимизацию эффективнее осуществить с помощью карт Карно, при этом в карты занести как единичные, так и нулевые значения наборов, имеющиеся в таблице. Это необходимо для того, чтобы в процессе минимизации было удобно доопределить функции.
3.5.5 Проводить минимизацию всех логических функций одновременно, чтобы получить в итоге как можно больше одинаковых наборов аргументов. Именно на этом этапе нужно воспользоваться возможностью доопределения функций.
4 ЛОГИЧЕСКИЙ СИНТЕЗ

ЦИФРОВОГО ВЫЧИСЛИТЕЛЬНОГО УСТРОЙСТВА.

ЛАБОРАТОРНАЯ РАБОТА № 4
4.1 Цель работы
Целью работы является приобретение практических навыков по анализу и синтезу цифровых устройств, способных решать практические задачи и содержащих типовые узлы различных модификаций.
4.2 Теоретические сведения
4.2.1 На практике нередко возникает задача выработки управляющих сигналов при произвольном порядке следования кодов этих сигналов. Произвольный порядок следования кодов можно осуществить с помощью счетчика с произвольным порядком счета, а выработку управляющих сигналов или, иными словами, расшифровку кодов – с помощью дешифратора. Таким образом, задача логического синтеза подобного устройства распадается на синтез счетчика с произвольным порядком счета и синтез дешифратора.
4.2.2 В теоретическом курсе дисциплины рассмотрены суммирующие двоичные счетчики с параллельным переносом. Работа одного из таких счетчиков с модулем счета Ксч = 8 описывается таблицей переходов – таблица 4.1. Подобные счетчики можно было бы еще назвать счетчиками с последовательным порядком счета, так как значение выходного кода в такте t+1 получается прибавлением единицы к младшему разряду кода в такте t. Любой иной порядок формирования выходного кода обеспечивают счетчики с произвольным порядком счета, причем последние не следует путать с вычитающими и реверсивными двоичными счетчиками. Последовательности значений трехразрядного кода 101, 110, 010, 011, 100, 001, 000, 111 соответствуют таблице переходов (таблица 4.2) счетчика, формирующего этот код.
Таблица 4.1 – Таблица переходов счётчика с последовательным счётом

x t	Q3 t	Q2 t	Q1 t	Q3 t+1	Q2 t+1	Q1 t+1	Выходной код счетчика
1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 1 1 1 0	0 1 1 0 0 1 1 0	1 0 1 0 1 0 1 0	0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Таблица 4.2 – Таблица переходов счётчика с произвольным счётом

x t	Q3 t	Q2 t	Q1 t	Q3 t+1	Q2 t+1	Q1 t+1	Выходной код счетчика
1 1 1 1 1 1 1 1	1 1 0 0 1 0 0 1	0 1 1 1 0 0 0 1	1 0 0 1 0 1 0 1	1 0 0 1 0 0 1 1	1 1 1 0 0 0 1 0	0 0 1 0 1 0 1 1	1 0 1 1 1 0 0 1 0 0 1 1 1 0 0 0 0 1 0 0 0 1 1 1

Для логического синтеза счетчиков с произвольным порядком счета можно применить табличный метод, как наиболее простой и наглядный.
4.2.3 Двоичный код, формируемый счетчиком, подается на вход дешифратора. Определение и назначение дешифратора даны в теоретическом курсе. Здесь обращается внимание на то, что дешифраторы могут быть линейные и пирамидальные. Если принимать во внимание только логические характеристики, то любую практическую задачу можно решить с помощью линейного дешифратора. Например, на рисунке 4.1 приведена схема линейного дешифратора трехразрядного кода, построенная в соответствии с таблицей состояний – таблица 4.3, где y_i – выходы дешифратора (i = 1, 2, ... , 8).
Таблица 4.3 – Таблица состояний линейного дешифратора

Входной код дешифратора	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	1 0 0 0 0 0 0 0	0 1 0 0 0 0 0 0	0 0 1 0 0 0 0 0	0 0 0 1 0 0 0 0	0 0 0 0 1 0 0 0	0 0 0 0 0 1 0 0	0 0 0 0 0 0 1 0	0 0 0 0 0 0 0 1

Примечание – синтез линейных дешифраторов рассмотрен в лекционном курсе.
Однако, ряд таких физических характеристик, как нагрузочная способность триггера (число логических элементов, одновременно подключаемых к одному выходу триггера); число входов логических элементов И-НЕ (ИЛИ-НЕ) и другое вынуждает применять пирамидальные дешифраторы.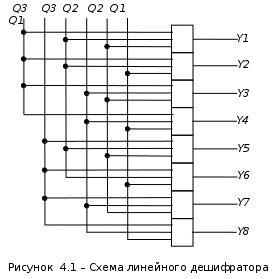


4.2.4 В основу синтеза пирамидального дешифратора положен следующий принцип построения:

а) рассматривается конечное число младших разрядов входного кода, как правило, равное двум, и для имеющихся комбинаций составляется таблица истинности, в которой каждая комбинация является выходной переменной первой ступени дешифратора;

б) на основании полученной в пункте (а) таблицы истинности синтезируется первая ступень дешифратора;

в) к двум младшим разрядам входного кода добавляется один следующий старший разряд и анализируется его конъюнктивная связь с выходными переменными первой ступени (в аналитической или графической форме), при этом каждая комбинация является выходной переменной второй ступени дешифратора;

г) на основании этого анализа синтезируется вторая ступень дешифратора;

д) к трем разрядам входного кода добавляется один следующий старший разряд и анализируется его конъюнктивная связь с выходными переменными второй ступени . . . и т. д., пока не будет рассмотрен последний старший разряд входного кода дешифратора.

Например, у трехразрядного кода Q₃, Q₂, Q₁, заданного таблицей 4.1, рассматриваем два младших разряда Q₂, Q₁, для которых составляем таблицу, учитывающую все имеющиеся комбинации – таблица 4.4.
Таблица 4.4 – Таблица состояний первой ступени пирамидального дешифратора

Q2	Q1	Комбинации	Z1	Z2	Z3	Z4
0 0 1 1	0 1 0 1	0 0 0 1 1 0 1 1	1 0 0 0	0 1 0 0	0 0 1 0	0 0 0 1

На основании данных таблицы 4.4 синтезируем первую ступень дешифратора, формирующую промежуточные переменные Z_i, подаваемые на входы второй ступени. Далее к двум младшим разрядам добавляем следующий, старший, и рассматриваем код Q₃, Q₂, Q₁ в соответствии с таблицей 4.3, где два младших разряда кода заменяем значениями Z_i:
Q₃Z₁ ; Q₃Z₂ ; Q₃Z₃ ; Q₃Z₄ ; Q₃Z₁ ; Q₃Z₂ ; Q₃Z₃ ; Q₃Z₄ .
В результате схема пирамидального дешифратора будет иметь вид рисунка 4.2.

Рассмотренный принцип синтеза пирамидального дешифратора позволяет использовать при его построении только двухвходовые конъюнкторы вне зависимости от разрядности дешифруемого кода. Другое достоинство заключается в уменьшении числа логических элементов, подключаемых одновременно к одному выходу триггера. Недостатком можно считать большое количество используемых логических элементов по сравнению с линейным дешифратором.

4.3 Формулировка задания
Синтезировать цифровое вычислительное устройство, вырабатывающее восемь управляющих сигналов при произвольном порядке следования кодовых комбинаций этих сигналов и содержащее счетчик и дешифратор. Задаются:

– тип триггеров счетчика;

– тип дешифратора;

– последовательность кодовых комбинаций сигналов, подлежащая выработке в указанном порядке, расшифровке и выдаче в цепи управления.

Предлагаются следующие варианты заданий:




– вариант 0. D - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃ Q₂Q₁, Q₃Q₂Q₁,Q₃ Q₂Q₁,

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁,Q₃ Q₂ Q₁,Q₃ Q₂ Q₁;

– вариант 1. JK - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁, Q₃ Q₂Q₁,Q₃Q₂Q₁,

Q₃ Q₂ Q₁, Q₃ Q₂Q₁,Q₃Q₂ Q₁,Q₃ Q₂ Q₁;

– вариант 2. D - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁, Q₃Q₂Q₁,Q₃Q₂Q₁,

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁,Q₃ Q₂ Q₁,Q₃Q₂ Q₁;

– вариант 3. JK - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁, Q₃Q₂Q₁,Q₃Q₂Q₁,

Q₃ Q₂ Q₁, Q₃ Q₂ Q₁,Q₃ Q₂ Q₁,Q₃Q₂Q₁;

– вариант 4. D - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂ Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃ Q₂Q₁,Q₃ Q₂Q₁,Q₃Q₂Q₁;
– вариант 5. JK - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁,Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 6. D - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 7. JK - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,

Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,Q₃Q₂Q₁;

– вариант 8. D - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂ Q₁, Q₃ Q₂Q₁,

Q₃Q₂Q₁, Q₃ Q₂ Q₁, Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 9. JK - триггер; дешифратор пирамидальный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁, Q₃Q₂ Q₁,Q₃ Q₂Q₁;

– вариант 10. JK - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁, Q₃Q₂ Q₁,Q₃ Q₂Q₁.

– вариант 11. D - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂ Q₁, Q₃ Q₂Q₁,

Q₃Q₂Q₁, Q₃ Q₂ Q₁, Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 12. JK - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,

Q₃Q₂Q₁, Q₃ Q₂Q₁, Q₃Q₂ Q₁,Q₃Q₂Q₁;

– вариант 13. D - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁, Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 14. JK - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃Q₂Q₁,Q₃ Q₂Q₁,Q₃Q₂Q₁;

– вариант 15. D - триггер; дешифратор линейный;

Q₃ Q₂ Q₁, Q₃Q₂ Q₁, Q₃Q₂Q₁,Q₃Q₂ Q₁,

Q₃ Q₂Q₁, Q₃ Q₂Q₁,Q₃ Q₂Q₁,Q₃Q₂Q₁;
4.4 Порядок выполнения работы
4.4.1 Выполняется при подготовке к работе:

– повторить разделы лекционного курса "Счетчики импульсов" и "Дешифраторы" и изучить теоретические сведения к данной лабораторной работе;

– сделать заготовку отчета по работе, где привести цель и по желанию выписки из теории.
4.4.2 Выполняется в лаборатории:

– получить у преподавателя номер варианта задания;

– в соответствии с заданным вариантом составить таблицу переходов счетчика и определить число входящих в него триггеров;

– по таблице переходов для каждого триггера счетчика составить карту переходов;

– с помощью карты переходов и матрицы переходов триггера для каждого его входа составить карту Карно;

– по каждому входу триггера (для JK - триггера по входам J и K, для D -триггера по входу D) выполнить минимизацию логических функций и записать их в виде функций возбуждения;

– в соответствии с полученными функциями возбуждения составить схему счетчика;

– выполнить синтез дешифратора. Выбираемая методика синтеза зависит от заданного типа дешифратора и может быть аналитической, табличной или комбинированной (на усмотрение студента);

– оформить отчет, куда поместить: вариант задания, все промежуточные и окончательные результаты синтеза счетчика и дешифратора, выводы по работе.
4.5 Методические указания по выполнению работы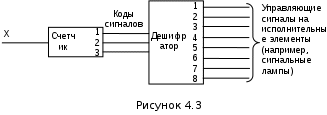

Функциональную схему синтезируемого цифрового вычислительного устройства можно представить в виде рисунка 4.3. Для синтеза счетчика с произвольным порядком счета может быть применен табличный метод без каких-либо корректировок. Его алгоритм подробно рассмотрен в ПРИЛОЖЕНИИ В. Здесь приводятся только матрицы переходов заданных типов триггеров (таблица 4.5 – для D - триггера и таблица 4.6 – для JK - триггера).