Физика ЛБ№1. Лабораторная работа 1 Изучение колебаний математического маятника
 Скачать 343.14 Kb.
|
|
Лабораторная работа №1 «Изучение колебаний математического маятника» I. Цель работы Наблюдения за колебательными движениями математического маятника, реализуемые на приборе, функциональная схема которого, представлена на рисунке 1. Измерение периода колебаний маятника при различных длинах и амплитудах. Определение режима изохронности колебаний математического маятника. Вычисление ускорения свободного падения шарика по результатам указанных измерений. II. Теоретическая часть Рассмотрим прибор, состоящий из шарика небольших размеров, прикреплённого к неподвижной точке подвеса с помощью невесомой нерастяжимой нити определённой длины. Если размеры шарика много меньше длины l нити, то шарик можно рассматривать как материальную точку; а если масса шарика много больше массы нити, то последнюю можно считать невесомой. Нить также можно считать нерастяжимой при условии, что сила тяжести шарика вызывает бесконечно малое удлинение нити. Данный прибор позволяет моделировать колебательные движения так называемого математического маятника. 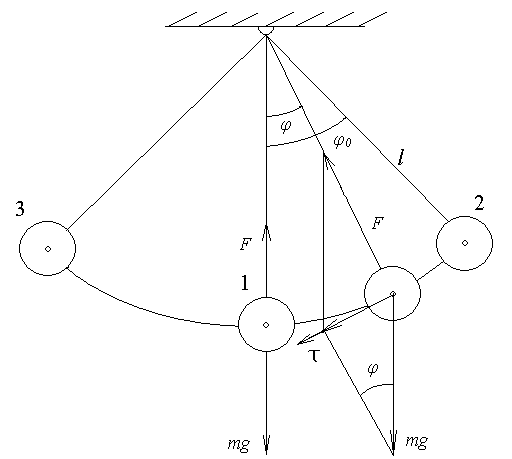 Рис.1 Действительно, в исходном состояние нить направлена вертикально вниз (положение 1 на рисунке 2). В этом случае сила F натяжения нити и сила mg тяжести шарика совпадают с направлением нити, но противоположно направлены. Так как нить нерастяжима, то обе силы уравновешивают друг друга, т.е. F = mg. Шарик находится в покое. Такое состояние маятника называется положением его равновесия. Очевидно, что траекторией движения шарика будет дуга окружности радиуса l. Такие движения называются колебаниями. Однако если наблюдать данный процесс в течение довольно короткого времени, то колебательный процесс можно признать незатухающим. maτ = - mgsin φ (1) Знак минус справа в (1) учитывает то обстоятельство, что при движении от положения равновесия вверх сила тяжести препятствует этому движению. Угловое ускорение ε шарика определяется как вторая производная по времени от угла φ, т.е.  (2)Между тангенциальным ускорением aτ и угловым ε имеет место очевидная связь    (3)Уравнение (1) с учётом формул (2) и (3) принимает вид:  (4)Такое уравнение в математике называют обыкновенным дифференциальным уравнением второго порядка. Его можно упростить, если учесть, что при малых углах φ, измеренных в радианах  . Тогда вместо (4) будем иметь (5)Уравнение (5) описывает движение маятника. Его ещё называют уравнением гармонического осциллятора. Таким образом, видно, что изменения угла φ по времени происходит по синусоидальному закону. Величина φ0, равная максимальному углу отклонения от положения равновесия, называется амплитудой гармонических колебаний. Величина амплитуды в данном случае зависит от первоначального отклонения. Величина же  стоящая под знаком синуса называется фазой. Фаза растёт пропорционально времени. Величина  под знаком синуса называется начальной фазой, которая в рассматриваемом движении равна нулю.Теперь с учётом  (6)  (7)для периода Т будем иметь:   (9)Такие колебания называются изохронными. Формулу (8) можно ещё представить так:  kl , (10)где через  (11)обозначен угловой коэффициент линейной функциональной зависимости функции T2 от аргумента l. Функциональная зависимость  , построенная по экспериментальным точкам, позволяет определить угловой коэффициент k, через числовое значение которого ускорение g свободного падения шарика вычисляется так: (12)Кроме того, по единичным измерениям T и l ускорение g можно вычислить ещё из такого соотношения:  (13)III. Порядок проведения эксперимента Так как линеаризация уравнения (4), приведшая к уравнению (5), описывающего изохронные колебания, основана на предположении, очевидно, что диапазон изохронности определяется значениями угла φ0 при которых имеет место линейная зависимость  .Следовательно, чтобы определить диапазон значений φ0 , при которых справедливо соотношение (10), необходимо для нескольких значений φ0 произвести измерения, позволяющие построить зависимости , далее из указанных функциональных зависимостей вычислить угловой коэффициент k и для выбранных углов φ0 вычислить значения g по (12), и сравнить их с общепринятым значением g = 9,8 м/с2. Те углы φ0, для которых вычисленная величина g с учётом погрешности измерений сохранит одинаковые числовые значения и определяет диапазон изохронности колебаний, реализуемых данным прибором.Порядок измерений таков: выбирается конкретное значение угла φ0, на которое необходимо отклонить шарик от положения равновесия, устанавливается длина маятника, производится опыт, в процессе которого измеряется период T. Опыт производится несколько раз так, что при фиксированном угле φ0 необходимо иметь от трёх до пяти измеренных значений l и T. Это будет первая серия измерений, которая на плоскости (T2l) даст только одну точку. Для проверки формулы (10) при данном угле φ0 необходимо произвести несколько таких серий. Предлагается сделать по пять таких серий измерений для каждого из углов φ0, в качестве которых выбираются следующие три угла: φ0 = 10о; φ0 = 20о; φ0 = 30о. По многократно измеренным значениям l и T для выбранного угла φ0 вычисляются их средние арифметические по формулам:  ,  , (14)IV. Обработка результатов измерений Любое из измеренных значений l и T, представленных в таблицах 1-3 не являются точными величинами, так как они измерены с определёнными погрешностями. В таких случаях в качестве точных значений указанных величин принимаются их средние арифметические, вычисляемые по формулам (14). Тогда под погрешностью измерения будем подразумевать модуль величины максимального отклонения всех измеренных величин от их среднего арифметического. А именно, погрешность ∆1 измерения длины маятника будем определять, как ∆1 = max |li - lср|(15) а погрешность ∆2 - периода колебаний маятника следует вычислять так: ∆2 = max |Ti – Tср| (16) В формулах (15) - (16) индекс i = 1,2,3 … пробегает все номера измерений соответствующих величин. Обработку результатов измерений будем производить на компьютере в программе Microsoft Excel и продемонстрируем технологию необходимых при этом расчётов на конкретных результатах измерений. А. (для φо = 10˚) Таблица 1.
Для каждой серии измерений необходимо по формулам (14) вычислить lср и Tср, а затем построить зависимость Tср2 = f(lср). Для удобства введём обозначения: Tср2 = y1, lср = x1. Таблица 2. 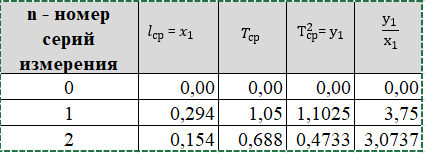 В этой таблице «lср=x1»-среднее арифметическое L для каждой серии измерений по формуле (14); «Tср» - среднее арифметическое Т для каждой серии измерений по формуле (14). Данные таблицы 2 позволяют с помощью программы Excel построить график функциональной зависимости y1 = f(x1).  Рис 1. Из рисунка 4 следует, что зависимость y1 = f(x1) имеет линейный характер и описывается уравнением y1 = 3,7419 x + 0,0357 (17) Уравнение 17 показывает, что угловой коэффициент k из уравнения (10) оказывается равным: k = 3,7419. Если это значение k подставить в формулу (12), то получим величину ускорения свободного падения. Угловой коэффициент k в уравнении (10) можно вычислить и из данных таблицы 4 по формуле 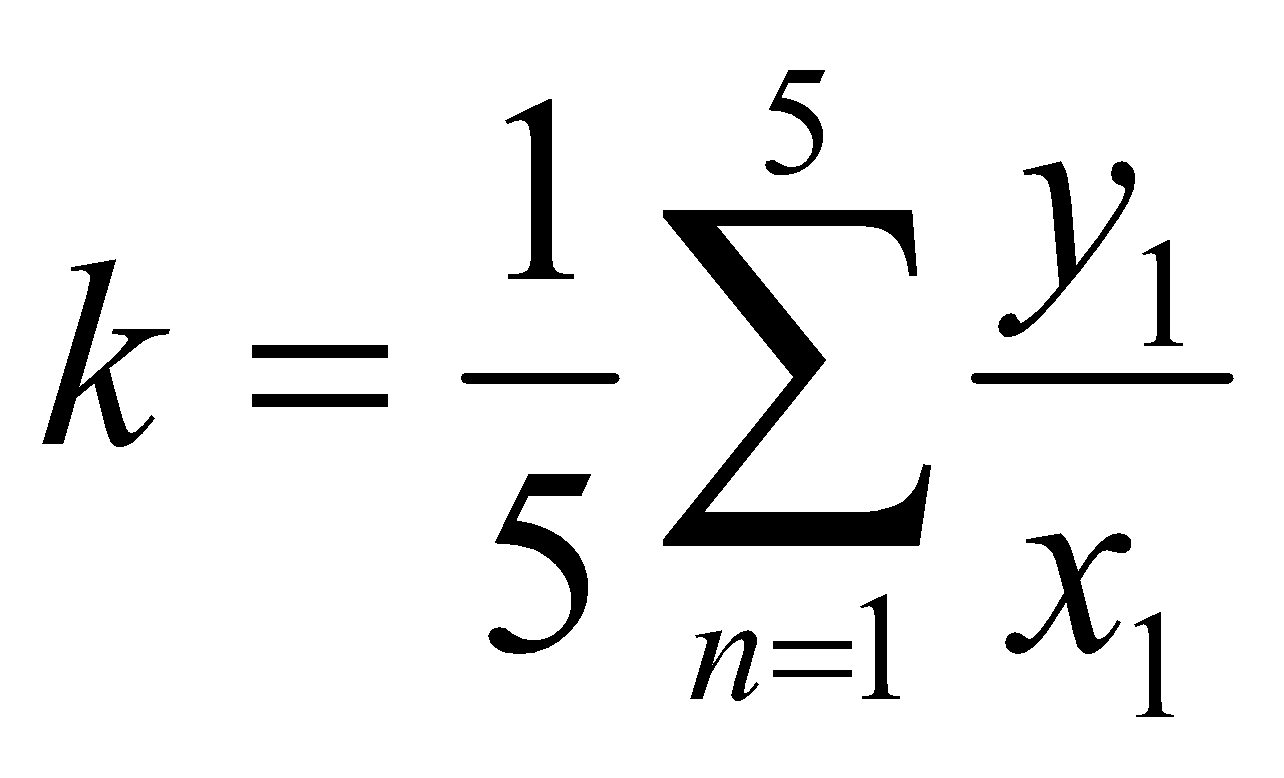 (18)получим k = 3,45048, т.е. число близкое к числу k, полученному из графика, изображённого на рисунке 4. Очевидно, что число  , полученное по формуле (12) с использованием величины k из уравнения (17) будет обладать некоторой погрешностью.Чтобы вычислить эту погрешность вернёмся к данным таблиц 1 и 2. При расчете формул (15) и (16) необходимо li и Ti, каждой серии измерений брать из таблицы 3, а lср и Tср из данных таблицы 1. Таблица 3.  Из данных таблицы 2 очевидно, что для каждой серии измерений точные значения длины l маятника и периода T колебаний маятника определяются так l = lср ± ∆1, T = Tср ± ∆2 (19) При этом оказывается, что ∆1 и ∆2 различны для каждой из длин маятника. Из формул (19) следует, что прямая линия рисунка 4 проведена с погрешностью и в её окрестности имеет место так называемый разброс экспериментальных данных. Чтобы учесть разброс опытных данных, вычислим ещё две функциональные зависимости: (Tср + ∆2)2 = f(lср + ∆1) (20) (Tср - ∆2)2 = f(lср - ∆1) (21) Для вычисления зависимости (20) введём новые обозначения: x2 = (lср + ∆1) (22) y2 = (Tср + ∆2)2 (23) Прежде чем приступить к вычислениям по формулам (22) и (23) образуем новую таблицу. При вычислении x2 и y2 по (22) и (23) необходимо пользоваться данными таблиц 2 и 3. Вначале вычисляем x2 и полученные числа заносим таблицу 4. Таблица 4. (Значение Х1 и У1 +∆) 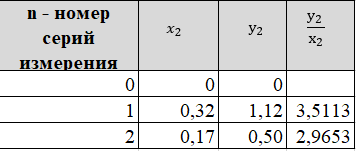 По данным таблицы строим график зависимости y2 = y2(x2) (см. рис. 5)  Рис.2 Из рисунка 5 видно, что зависимость y2 = y2(x2) определяется уравнением y2 = 3,254984 x2 +0,0546 (24) Переходим к вычислению функциональной зависимости (21). Для этого введём две вспомогательные формулы x3 = lср - ∆1 (5) y3 = (Tср - ∆2)2(26) Вычисление по этим формулам производится по данным таблиц 3 и 4, а результаты указанных вычислений заносятся в таблицу 8. Таблица 5. (Значение Х1 и У1 +∆)  Функциональная зависимость y3 = y3(x3), построенная по данным таблицы 6 указана на рисунке 6. 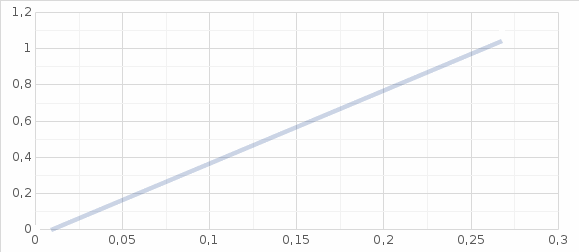 Рис.3 Из рисунка 6 следует, что y3 = 3,695288 x3 + 0,0162 (27) Значения углового коэффициента k по данным уравнений (17), (24), (27) заносим в таблицу 5. Таблица 6. 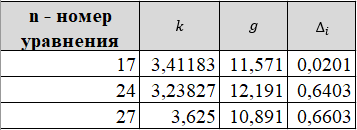 Для получения g используем формулу (12), соответствующую каждому значению k. Теперь вычисляем среднее значение g по формуле 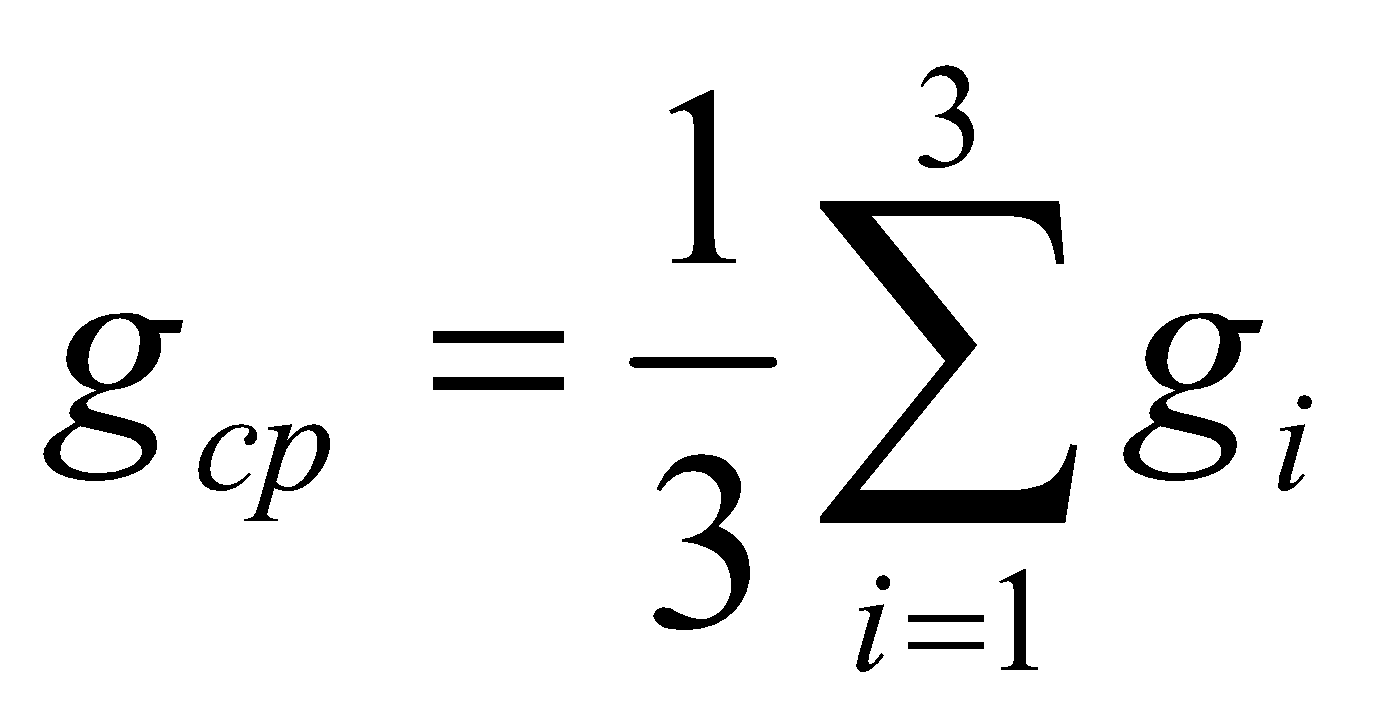 Оно оказывается равным 11,41794, которое принимаем за точное значением. Погрешность определения данного значения g вычисляем по формуле Δ3 = max |gi – gср| = max |Δi| (28) Из данных таблицы 6 следует, что Δ3 =0,42665. Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным: g =11,41794 ± 0,734491 Б. (для φо = 20˚) Таблица 7.  Для каждой серии измерений необходимо по формулам (14) вычислить lср и Tср, а затем построить зависимость Tср2 = f(lср). Для удобства введём обозначения: Tср2 = y1, lср = x1. Таблица 8. 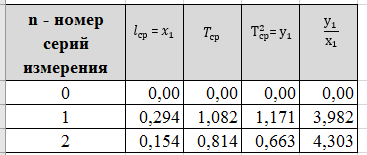 В этой таблице «lср=x1»-среднее арифметическое L для каждой серии измерений по формуле (14); «Tср» - среднее арифметическое Т для каждой серии измерений по формуле (14). Данные таблицы 8 позволяют с помощью программы Excel построить график функциональной зависимости y1 = f(x1). 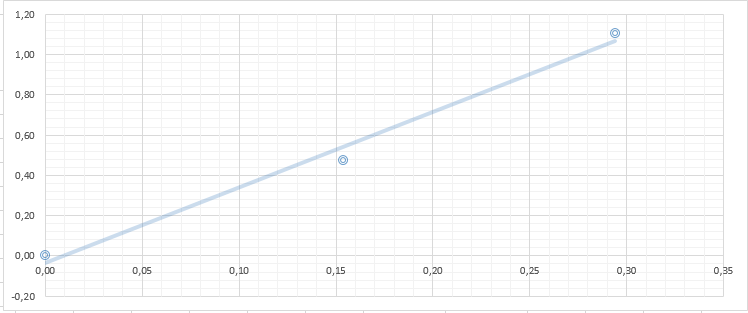 Рис.4 Из рисунка 4 следует, что зависимость y1 = f(x1) имеет линейный характер и описывается уравнением y1 = 3,74 x + 0,05 (17) Уравнение 17 показывает, что угловой коэффициент k из уравнения (10) оказывается равным: k = 3,74. Если это значение k подставить в формулу (12), то получим величину ускорения свободного падения. Угловой коэффициент k в уравнении (10) можно вычислить и из данных таблицы 4 по формуле (18) получим k = 4,142312925, т.е. число близкое к числу k, полученному из графика, изображённого на рисунке 4. Очевидно, что число, полученное по формуле (12) с использованием величины k из уравнения (17) будет обладать некоторой погрешностью. Чтобы вычислить эту погрешность вернёмся к данным таблиц 6 и 7. Таблица 9.  При расчете формул (15) и (16) необходимо li и Ti, каждой серии измерений брать из таблицы 8, а lср и Tср из данных таблицы 9. Из данных таблицы 9 очевидно, что для каждой серии измерений точные значения длины l маятника и периода T колебаний маятника определяются так l = lср ± ∆1, T = Tср ± ∆2 (19) При этом оказывается, что ∆1 и ∆2 различны для каждой из длин маятника. Из формул (19) следует, что прямая линия рисунка 7 проведена с погрешностью и в её окрестности имеет место так называемый разброс экспериментальных данных. Чтобы учесть разброс опытных данных, вычислим ещё две функциональные зависимости: (Tср + ∆2)2 = f(lср + ∆1) (20) (Tср - ∆2)2 = f(lср - ∆1) (21) Для вычисления зависимости (20) введём новые обозначения: x2 = (lср + ∆1) (22) y2 = (Tср + ∆2)2 (23) Прежде чем приступить к вычислениям по формулам (22) и (23) образуем новую таблицу 9. При вычислении x2 и y2 по (22) и (23) необходимо пользоваться данными таблиц 8 и 9. Вначале вычисляем x2 и полученные числа заносим таблицу 7. Таблица 10. (Значение Х1 и У1 +∆) 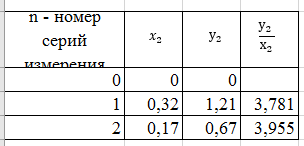 По данным таблицы 10 строим график зависимости y2 = y2(x2)  Рис.5 Из рисунка 8 видно, что зависимость y2 = y2(x2) определяется уравнением y2 = 3,868272059x2+0,0437 (24) Переходим к вычислению функциональной зависимости (21). Для этого введём две вспомогательные формулы x3 = lср - ∆1 (25) y3 = (Tср - ∆2)2 (26) Вычисление по этим формулам производится по данным таблиц 9 и 10, а результаты указанных вычислений заносятся в таблицу 11. Таблица 11. (Значение Х1 и У1 +∆) 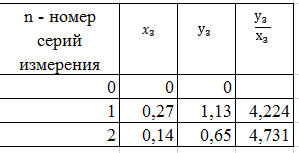 Функциональная зависимость y3 = y3(x3), построенная по данным таблицы 11 указана на рисунке 6. 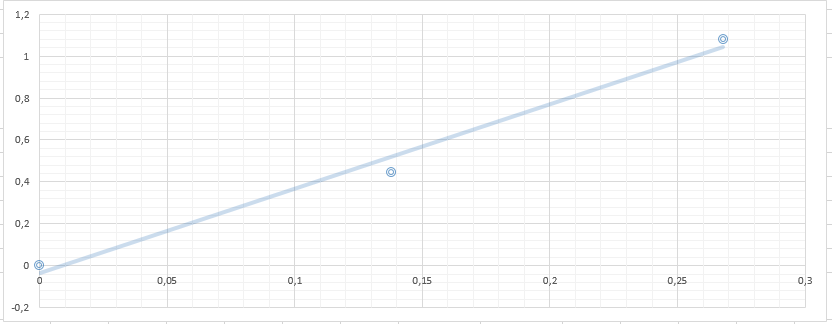 Рис.6 Из рисунка 6 следует, что y3 = 4,477568678 x3 + 0,0552 (27) Значения углового коэффициента k по данным уравнений (17), (24), (27) заносим в таблицу. 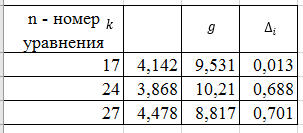 Для получения g используем формулу (12), соответствующую каждому значению k. Теперь вычисляем среднее значение g по формуле Оно оказывается равным 9,517718422, которое принимаем за точное значением. Погрешность определения данного значения g вычисляем по формуле Δ3 = max |gi – gср| = max |Δi| (28) Из данных таблицы 11 следует, что Δ3 = 0,700786636. Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным: g = 9,517718422 ± 0,700786636 В. (для φ=30˚) Таблица 12. 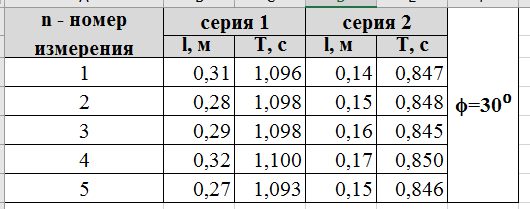 Для каждой серии измерений необходимо по формулам (14) вычислить lср и Tср, а затем построить зависимость Tср2 = f(lср). Для удобства введём обозначения: Tср2 = y1, lср = x1. Таблица 13.  В этой таблице «lср=x1»-среднее арифметическое L для каждой серии измерений по формуле (14); «Tср» - среднее арифметическое Т для каждой серии измерений по формуле (14). Данные таблицы 13 позволяют с помощью программы Excel построить график функциональной зависимости y1 = f(x1). Рис.7  Рис.7 Из рисунка 7 следует, что зависимость y1 = f(x1) имеет линейный характер и описывается уравнением: Угловой коэффициент k в уравнении (10) можно вычислить и из данных таблицы 13 по формуле (18) получим k = 4,376964075, т.е. число близкое к числу k, полученному из графика, изображённого на рисунке 7. Очевидно, что число, полученное по формуле (12) с использованием величины k из уравнения (17) будет обладать некоторой погрешностью. Чтобы вычислить эту погрешность вернёмся к данным таблиц 12 и 13. Таблица 14. 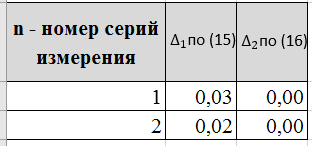 l = lср ± ∆1, T = Tср ± ∆2 (19) При этом оказывается, что ∆1 и ∆2 различны для каждой из длин маятника. Из формул (19) следует, что прямая линия рисунка 10 проведена с погрешностью и в её окрестности имеет место так называемый разброс экспериментальных данных. Чтобы учесть разброс опытных данных, вычислим ещё две функциональные зависимости: (Tср + ∆2)2 = f(lср + ∆1) (20) (Tср - ∆2)2 = f(lср - ∆1) (21) Для вычисления зависимости (20) введём новые обозначения: x2 = (lср + ∆1) (22) y2 = (Tср + ∆2)2 (23) Прежде чем приступить к вычислениям по формулам (22) и (23) образуем новую таблицу 15. При вычислении x2 и y2 по (22) и (23) необходимо пользоваться данными таблиц. Вначале вычисляем x2 и полученные числа заносим таблицу 15. Таблица 15. (Значение Х1 и У1 +∆)  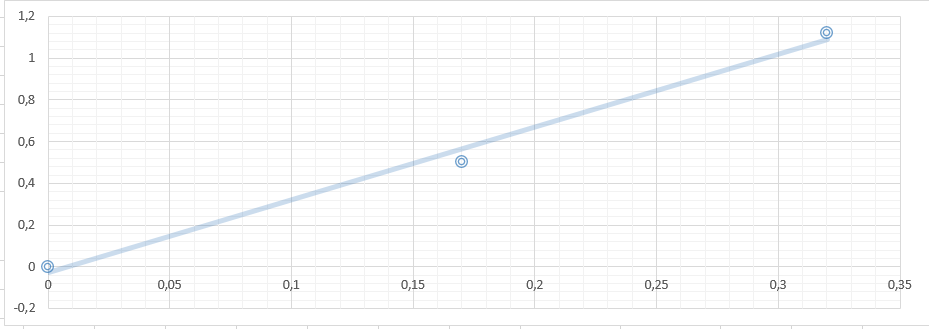 Рис 8. Из рисунка 8 видно, что зависимость y2 = y2(x2) определяется уравнением y2 = 4,018x + 0,0284 (24) Переходим к вычислению функциональной зависимости (21). Для этого введём две вспомогательные формулы x3 = lср - ∆1 (25) y3 = (Tср - ∆2)2 (26) Вычисление по этим формулам производится по данным таблиц 13 и 14, а результаты указанных вычислений заносятся в таблицу 16. Таблица 16. (Значение Х1 и У1 -∆) 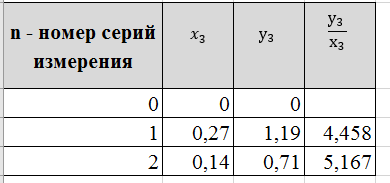 Функциональная зависимость y3 = y3(x3), построенная по данным таблицы 16 указана на рисунке 9.  Рис.9 Из рисунка 9 следует, что y3= 4,812197254 x + 0,0405 (27) Значения углового коэффициента k по данным уравнений (17), (24), (27) заносим в таблицу 17. Таблица 17. 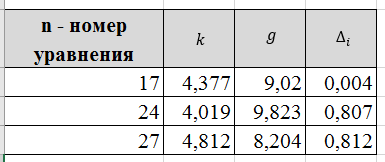 Для получения g используем формулу (12), соответствующую каждому значению k. Теперь вычисляем среднее значение g по формуле Оно оказывается равным 9,0154, которое принимаем за точное значением. Погрешность определения данного значения g вычисляем по формуле Δ3 = max |gi – gср| = max |Δi| (28) Из данных таблицы 17 следует, что Δ3 = 0,811576894. Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным: g = 9,0154 ± 0,811576894 V. Выводы Таким образом, после проведенных расчетов для каждого угла мы смогли определить значение g учитывая погрешность измерений. Для более точного ответа я решила посчитать среднее арифметическое g со всех 3 углов. Для этого воспользуемся формулой: 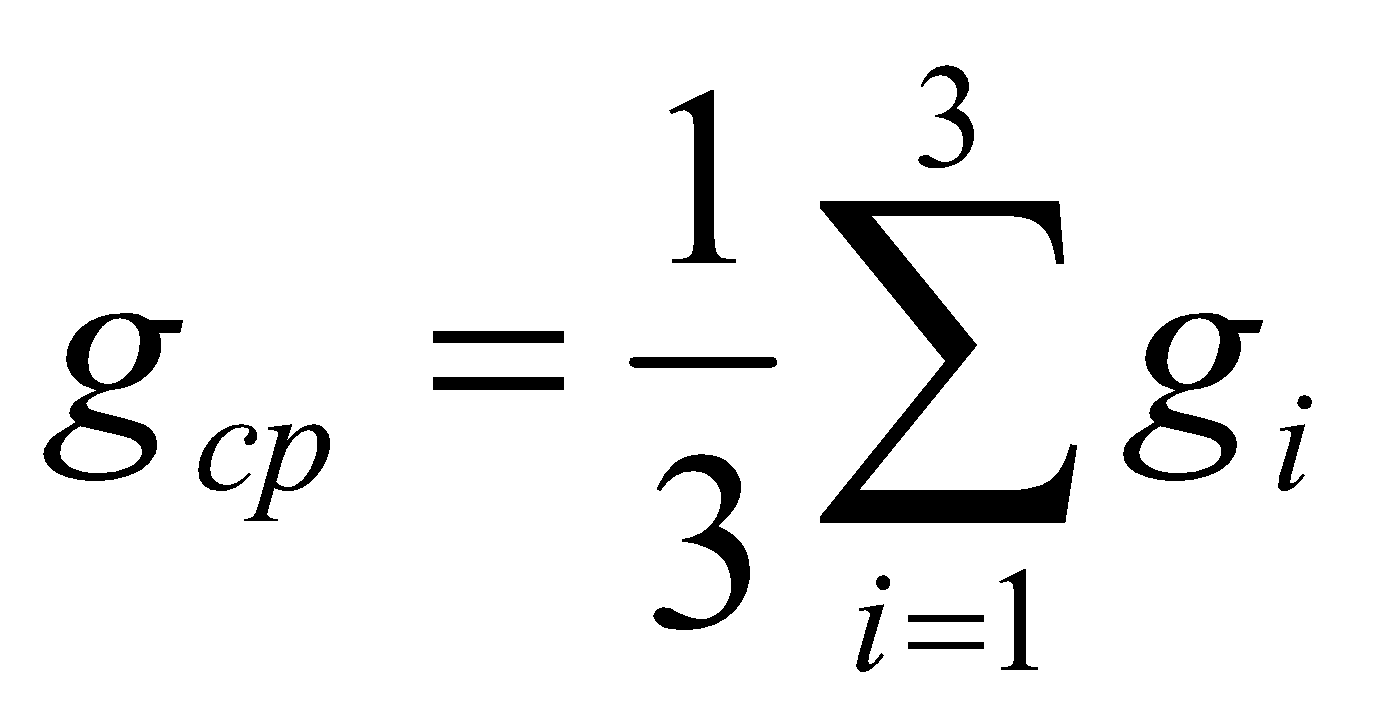Произведя расчеты получаем: g ср = 10,028 Погрешность определения данного значения g вычисляем по формуле: Δ3 = max |gi – gср| = max |Δi| (28) Δ3= 0,724 Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным: g =10,028 ± 0,724. Колебания являются изохронными. Ответы на контрольные вопросы: Из каких элементов состоит прибор для изучения колебаний математического маятника. Ответ: Математический маятник - это идеализированная система, состоящая из невесомой и нерастяжимой нити длины l, на которой подвешен шарик массы т, сосредоточенной в одной точке (так как размеры шарика 𝑑 ≪ 𝑙). Изохронное колебание – это колебания, период которых не зависят от амплитуды Математический маятник - это материальная точка, подвешенная на невесомой и нерастяжимой нити. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь. Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником. Причинами свободных колебаний математического маятника являются: 1. Действие на маятник силы натяжения и силы тяжести, препятствующей его смещению из положения равновесия и заставляющей его снова опускаться. 2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше. . Период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник. Период свободных колебаний математического маятника На базе какого закона механики составляется уравнение движения маятника. Ответ: Это уравнение образуется из уравнения движения mW=F+N где F - действующая на точку активная сила, а N - реакция связи. Второй закону Ньютона, дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. При каких ограничениях получается уравнение, моделирующее движение математического маятника. Ответ: 1) амплитуда колебаний мала (мал угол отклонения) ; 2) нет сопротивления воздуха; 3) вес нити, по сранению с весом грузика мал; 4) тело маленькое , (не работает собственный момент инерции) ; Все зависит от требуемой точности решения. 1) Нить не растяжима.2) Тело на подвесе считаем материальной точкой. Какие колебания называются гармоническими. Ответ: Величина φ0, равная максимальному углу отклонения от положения равновесия, называется амплитудой гармонических колебаний. Дайте определение амплитуды, фазы и частоты колебаний. Ответ: Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия. Величина φ0, равная максимальному углу отклонения от положения равновесия, называется амплитудой гармонических колебаний. Величина амплитуды в данном случае зависит от первоначального отклонения. Величина же стоящая под знаком синуса называется фазой. Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с. Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно. | |||||||||||||||||||||||||||||||||||