ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы

• Название: Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
• Дата: 20.04.2018
• Размер: 1.61 Mb.
• Имя файла: ФИНАНСОВЫЕ ФУНКЦИИ лаб работы.docx
• Тип: Лабораторная работа; #41737
• страница: 11 из 14

ЛАБОРАТОРНАЯ РАБОТА № 11
Решение задач методом оптимизации

Цель работы: изучение методики решения задач линейного программирования с использованием инструмента поиск решения.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Прежде чем обращаться к инструменту поиск решения, нужно проанализировать задачу и построить математическую модель. Для построения модели необходимо:

а) определить, каковы переменные модели;

б) выбрать целевую функцию;

в) задать ограничения, которым должны удовлетворять переменные.

При подготовке рабочего листа к решению задачи нужно:

1. 
   Отвести диапазон ячеек для хранения переменных величин.
   
2. 
   В отдельную ячейку ввести функцию цели. Функция цели всегда зависит от переменных, поэтому в ячейке с целевой функцией будут использованы ссылки на ячейки, где хранятся переменные.
   
3. 
   Подготовить значения и формулы для задания ограничений. Поскольку ограничения накладываются на переменные, то в формулах для задания ограничений будут использованы ссылки на ячейки, где хранятся переменные.
   

Рисунок 40 – Окно диалога Поиск решения
После построения математической модели можно обратиться к средству поиск решения. Для этого нужно воспользоваться командой Данные → Анализ → Поиск решения. (Если эта команда недоступна, то нужно выполнить такую последовательность действий: Кнопка Office → Параметры Excel → Надстройки → Перейти и установить флажок Поиск решения.) Появится окно диалога Поиск решения (рисунок 40).

В поле Установить целевую ячейку нужно указать ссылку на ячейку с целевой функцией. Если перед вызовом инструмента поиск решения выделить ячейку с целевой функцией (рекомендуется), то это поле уже будет заполнено.

Ниже расположены элементы управления – переключатели, позволяющие задать значение целевой функции, которое должно быть достигнуто при решении задачи: минимальное, максимальное или некоторое конкретное значение.




Рисунок 41 – Окно диалога для задания
ограничений
Поле Изменяя ячейки позволяет задать диапазон, в котором располагаются неизвестные величины, влияющие на целевую функцию.

Список Ограничения представляет все ограничения, накладываемые на переменные. Чтобы добавить ограничение, нужно воспользоваться кнопкой Добавить. На экране появится диалоговое окно (рисунок 41).

Поле Ссылка на ячейку появившегося окна предназначено для указания ссылки на ячейки, где хранятся переменные или формулы, используемые для задания ограничений. В поле Ограничение можно задать константу, ссылку на ячейки со значениями или формулами. Значения из полей Ссылка на ячейку и Ограничение сравниваются с помощью операций (>=, <=, =, цел, двоич), которые можно выбрать из списка, расположенного между этими двумя полями.

Кнопка Добавитьпозволит задать несколько ограничений, кнопка ОКдобавляет ограничение и закрывает это окно.

Кнопка Изменитьдиалогового окна Поиск решения позволяет модифицировать выделенное в списке Ограничения ограничение. При этом на экране появится диалоговое окно Добавление ограничения (см. рисунок 57) с уже заполненными элементами управления.

Кнопка Удалитьдиалогового окна Поиск решения позволяет удалить выделенное ограничение.

После того как все данные для инструмента поиск решения будут заданы, следует воспользоваться кнопкой Выполнить. Если решение будет найдено, Excel выдаст об этом сообщение и результаты расчета задачи будут помещены в соответствующие ячейки. Если решение не может быть найдено, то Excel также выдаст об этом сообщение.

Чтобы изменить параметры поиска решения исследуемой задачи, нужно воспользоваться кнопкой Параметрыдиалогового окна Поиск решения для вызова окна диалога Параметры поиска решения, в котором можно произвести настройку необходимых опций для осуществления поиска решения.

ПРАКТИКУМ

Задача 1. Планом развития региона предполагается ввести в действие 3 нефтяных месторождения с суммарным объемом добычи, равным 9 млн. т. На первом месторождении объем добычи составляет не менее 1 млн. т, на втором – 3 млн. т, на третьем – 5 млн. т. Для достижения такой производительности необходимо пробурить не менее 125 скважин. Для реализации данного плана выделено 25 млн. руб. капитальных вложений (показатель К) и 80 км труб (показатель L). Требуется определить оптимальное (максимальное) количество скважин для обеспечения максимальной производительности всех месторождений. Исходные данные задачи приведены в таблице 10.

Таблица 10 – Исходные данные задачи

Месторождение	Добыча, млн.т	Фонд скважин	Дебет 1 скважины	Длина трубопровода для 1 скважины	Стоимость строительства 1 скважины	К	L
1	1	10	100	1,0	300
2	3	15	200	2,0	200
3	5	100	50	0,5	150
Итого:	9	125	350			25,0	80,0

Алгоритм решения задачи

Целью решения данной оптимизационной задачи является нахождение максимального значения добычи нефти при оптимальном количестве скважин для каждого месторождения с учетом существующих в задаче ограничений.

Целевая функция в соответствии с требованиями задачи примет вид

100*Х₁+200*Х₂+50*Х₃→mах,

где X₁, Х₂, и X₃, — количество скважин для каждого месторождения, коэффициенты при неизвестных представляют собой производительность скважин.

Выполним формализацию существующих в задаче ограничений в виде системы неравенств следующего вида:

• ограничения на длину прокладки труб:

Х₁+2·Х₂+0,5Х₃≤80;

• ограничения на число скважин на каждом месторождении:

X₁≤10;

Х₂≤15;

Х_з≤100;

• ограничения по капитальным вложениям по всему месторождению с учетом стоимости на одну скважину:

0,3·X₁ +0,2·X₂ + О,15Х₃≤25.

Решение задачи в системе Excel опишем в несколько этапов, и начнем с представления и формирования исходных данных.

• начальные значения искомых переменных поместить в ячейки с адресами С9, D9, Е9;

• значения единичной добычи поместить в ячейки С7, D7, Е7;

• в ячейку В11 поместить целевую функцию C7*C9+D7*D9+E7*E9;

• значения протяженности трубопровода для строительства одной скважины ввести в ячейки С5, D5, Е5;

• стоимость строительства скважины ввести в ячейки С6, D6, Е6;

• формулу расчета общей протяженности C5*C9+D5*D9+E5*E9 поместить в ячейку В5;

• формулу расчета общей стоимости C6*C9+D6*D9+E6*E9 сформировать в ячейке В6;

• тип ограничений ввести в ячейки F5, F6;

• значения ограничений ввести в ячейки G5, G6;

• ограничения количества скважин С8, D8, Е8.

Исходные данные для решения задачи приведены в виде таблицы описания математической модели на рисунке 42.




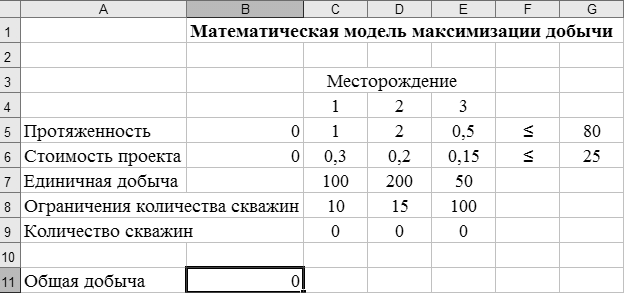
Рисунок 42 – Таблица описания математической модели задачи



Для решения задачи будем использовать модуль Поиск решения, который находится на вкладке Анализ ленты Данные. Следует заметить, что опция Поиск решения оперирует с тремя основными компонентами построенной оптимизируемой модели. Таким образом, исходная задача описывается в виде матрицы (см. рисунок 42).




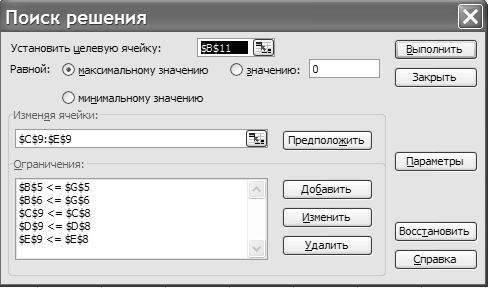
Рисунок 43 – Окно диалога Поиск решения с
решением задачи
В диалоговом окне Поиск решения (см. рисунок 43) требуется задать необходимые параметры. В поле Установить целевую ячейку нужно указать адрес ячейки, которая содержит формулу для расчета целевой функции. Очень важно, чтобы эта формула была связана с изменяемыми ячейками, выражающими искомые переменные задачи – в нашем примере ячейка В11. В поле Изменяя ячейки ввести область, содержащую изменяемые ячейки – С9:Е9. Кнопкой Добавить вызвать диалоговое окно Добавление ограничения (см. рисунок 41) и сформировать в нем 5 ограничений: ограничение на длину труб, ограничение по капитальным вложениям и 3 ограничения на число скважин. Кнопкой Параметры открыть диалоговое окно Параметры поиска решения и задать переключатель Линейная модель и нажать копку ОК. Диалоговое окно Поиск решения с результатом решения задачи примет вид (рисунок 44).




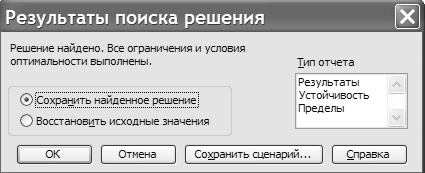
Рисунок 44 – Диалоговое окно
Результаты поиска решения
Запуск на решение модели и вычисления результатов осуществляется нажатие кнопки Выполнить. В строке состояния будут отображены некоторые шаги процесса вычислений. После окончания поиск решения завершен, новые значения будут вставлены в таблицу, а на экране появится диалоговое окно Результаты поиска решения которое будет содержать информацию о завершении процесса поиска решения, (рисунок 44). Здесь можно указать, должен ли быть представлен в таблице новый результат и нужно ли составить отчет. Если установлена опция Восстановить исходные значения и не задано составление отчета, то найденные значения будут удалены. При задании режима составления отчета следует выбрать тип отчета в поле Тип отчета (отчет по результатам, отчет по устойчивости и отчет по пределам) и нажать ОК.

Таким образом, программа выполнила расчет определения оптимального количества скважин для обеспечения плановой производительности каждого месторождения (Количество скважин и Общая добыча на рисунке 45).



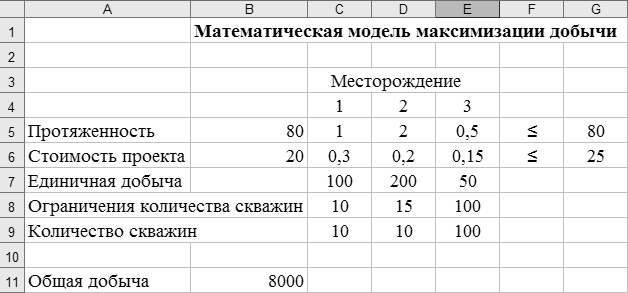
Рисунок 45 – Решение модели по параметрам Общая добыча и
Количество скважин



Задача 2. Задача максимизации прибыли. Предприятие выпускает 4 вида продукции: П1, П2, ПЗ, П4. Для ее изготовления используется 3 вида ресурсов: p1, р2, р3, объем которых ограничен. Известны потребность в ресурсах для каждого вида продукции, а также прибыль, получаемая от ее реализации. Требуется определить оптимальное количество выпуска каждого вида продукции, при котором будет получена максимальная прибыль для предприятия. Исходные данные представлены в таблице 11.

Таблица 11 – Исходные данные

Показатель	Виды продукции				Тип огранич.	Знач., огранич.
	П1	П2	П3	П4
Един. прибыльРесурс p1 Ресурс р2 Ресурс рЗ	60 1 4 6	70 1 6 5	120 1 10 4	130 1 13 3	≤ ≤ ≤	16 100 110
Нижняя граница	1	2	2	1
Верхняя граница	4	-	-	1

Алгоритм решения задачи

Разработаем математическую модель задачи.

Целевая функция:

60*n1 + 70*n2 + 120*n3 + 130*n4 → mах

1. Введем в таблицу исходные данные:

• 
  начальные значения искомых переменных (П1-П4) разместить в ячейках В6:Е6;
  
• 
  значения единичной прибыли – в ячейках В7:Е7;
  
• 
  нормы расходов ресурсов (p1-р3) на каждый вид продукции поместить соответственно в ячейки В10:В12 для П1, С10:С12 для П2; D10:D12 для П3; Е10:Е12 дляП4;
  
• 
  в ячейку G5 ввести целевую функцию В7*B6+С7*C6+D7*D6+E7*E6;
  
• 
  задать формулы подсчета объема потребления каждого вида ресурса:
  

• 
  в ячейке Н10 для p1 B10*B6+C10*C6+D10*D6+E10*E6;
  
• 
  в ячейке Н11 для р2 B11*B6+C11*C6+D11*D6+E11*E6;
  
• 
  в ячейке Н12 для р3 B12*B6+C12*C6+D12*D6+E12*E6;
  

• 
  тип ограничений помещается в ячейки F10:F12, значения ограничений – в ячейки G10:G12;
  
• 
  граничные условия задаются в ячейках: В14:Е14 – значения нижних границ В15:Е15 – значения верхних границ.
  

Исходные данные представлены на рисунке 46.




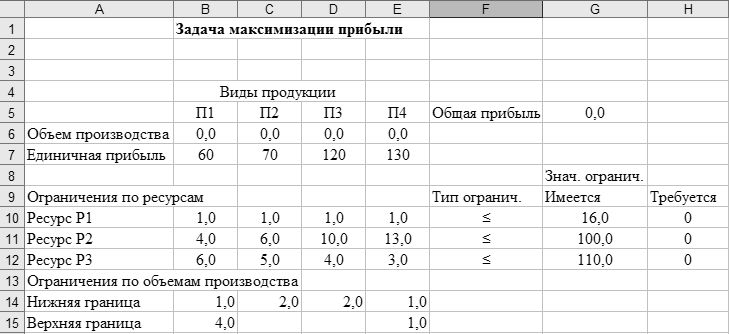
Рисунок 46– Таблица описания математической модели задачи


После формирования исходных данных откроем диалоговое окно Поиск решения (рисунок 47) и введем необходимые значения целевой функции, изменяемых ячеек, ограничений, в поле Параметры выберем Линейную модель, нажмем ОКи Выполнить.

Таким образом, получен результат: программа определила значения объемов производства для каждого вида продукции и соответствующее значение целевой функции, выражающее получаемую при этом прибыль (таблица решения на рисунке 48).




Рисунок 48 – Результат решения задачи максимизации прибыли



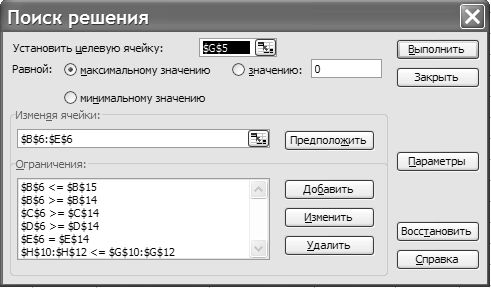
Рисунок 47 – Диалоговое окно Поиск решения для
задачи максимизации прибыли


Задача 3.