|
|
ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
ЛАБОРАТОРНАЯ РАБОТА № 2
Оценка инвестиционных проектов
Цель работы: изучение функций, использующихся при оценке инвестиционных проектов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
При оценке инвестиционных проектов используются функции текущей стоимости, чистой текущей стоимости, внутренней ставки доходности, индекс рентабельности.
Понятие текущей (современной) стоимости будущих доходов и расходов базируется на положении о том, что на начальный момент времени полученная в будущем сумма денег имеет меньшую стоимость, чем ее эквивалент, полученный в начальный момент времени. Согласно концепции временной стоимости денег, расходы и доходы, не относящиеся к одному моменту времени, можно сопоставить путем приведения к одному сроку (т. е. путем дисконтирования). Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени.
Excel содержит ряд функций, которые позволяют рассчитать:
текущую стоимость единой суммы вклада (займа) и фиксированных периодических платежей (функция ПС);
чистую текущую стоимость будущих периодических расходов и поступлений переменной величины (функция ЧПС).
Заметим, что расчеты с использованием функций ПС и ЧПС являются частными случаями вычисления текущей стоимости ожидаемых доходов и расходов, которые в общем случае могут быть переменной величиной и происходить в разные периоды времени. Расчет при помощи функции ПС требует денежных потоков равной величины через равные интервалы между операциями. Функция ЧПС доводит денежные потоки переменной величины через равные периоды времени.
Функция ПС предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Этот расчет является обратным к определению будущей стоимости при помощи функции БС.
Синтаксис ПС(ставка;кпер;плт;бс;тип).
Эта функция может быть полезна в следующих расчетах:
1. Допустим, известно будущее (наращенное) значение вклада (займа). Требуется определить текущее значение этого вклада, т. е. сумму, которую необходимо положить на счет сегодня, чтобы в конце n-го периода она достигла заданного значения. Это значение можно получить из формулы (1):
 . (5) . (5)
Такой же расчет при использовании функции ПС в общем виде запишется так: =ПС(ставка;кпер;;бс;).
2. Предположим теперь, что требуется найти текущую стоимость будущих периодических постоянных платежей, которые производятся в начале или в конце каждого расчетного периода. Согласно концепции временной стоимости, чем дальше от настоящего момента будет поступление или расходование средств, тем меньшую текущую ценность оно представляет. Таким образом, при равных условиях текущая стоимость вкладов пренумерандо больше, чем текущая стоимость вкладов постнумерандо.
Расчет текущей стоимости серии будущих постоянных периодических платежей, пренумерандо каждого периода и дисконтированных нормой дохода r, ведется по формуле:
 , (6) , (6)
где pv – текущая стоимость фиксированных периодических платежей;
pmt – фиксированная периодическая сумма платежа;
п – общее число периодических выплат (поступлений);
r – постоянная процентная ставка.
В общем виде для решения этой задачи функция имеет вид =ПС(ставка;кпер;плт;;1)
Для расчета текущей стоимости постоянных периодических выплат постнумерандо формулу (6) следует модифицировать:
 (7) (7)
Соответствующая этому расчету функция в Excel имеет вид: =ПС(ставка;кпер;плт;;). По умолчанию аргумент тип = 0, поэтому его можно не указывать.
Функция ЧПС вычисляет чистую текущую стоимость (NPV) периодических платежей переменной величины как сумму ожидаемых доходов и расходов, дисконтированных нормой процента r. Формула для вычисления (NPV):
 , (8) , (8)
где NPV– чистая текущая стоимость периодических выплат и поступлений;
r– норма дисконтирования (средняя цена капитала);
п – количество выплат и поступлений;
value– значение выплат и поступлений.
Метод определения чистой текущей стоимости часто применяется при оценке эффективности инвестиций. Он позволяет определить нижнюю границу прибыльности и использовать ее в качестве критерия при выборе наиболее эффективного проекта. Дисконтирование ожидаемых доходов и расходов позволяет учесть издержки привлечения капитала. Положительное значение NPVявляется показателем того, что проект приносит чистую прибыль своим инвесторам после покрытия всех связанных с ним расходов. Если NPV < 0, то заданная норма прибыли не обеспечивается и проект убыточен. Если NPV = 0 – инвестиции окупаются, но проект не приносит сверхприбыли.
Свойства NPV
Аддитимности 
Чем выше процентная ставка (норма дисконта) тем ниже NPV.
Чем выше r тем больше срок окупаемости n.
Чем больше платежей поступает вначале экономической жизни проекта тем больше NPV
Синтаксис: ЧПС(ставка;значение1;значение2;. . . ;значениеN).
Считается, что инвестиция, чистую текущую стоимость которой вычисляет функция ЧПС, начинается за один период до даты аргумента значение 1 и заканчивается с последним значением в списке. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить (вычесть, если это затраты) к результату функции ЧПС, но не включать в список аргументов.
Для выбора наиболее эффективного проекта из нескольких предложенных при ограниченном инвестиционном бюджете целесообразно использовать индекс рентабельности (Profitability index PI):
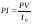 , (9) , (9)
где PV – текущая (современная стоимость);
I0 – первоначальные инвестиции.
Экономический смысл – показывает сколько единиц современной величины денежного потока приходится на единицу предполагаемых затрат.
Правила:
Если PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивает тем самым наличие положительной величины NPV. И проект следует принять.
Если PI = 1, то величина NPV равна первоначальным инвестициям, т. е. инвестиции окупаются, но проект не приносит сверхприбыли
Если PI < 1, то проект не обеспечивает заданного уровня рентабельности и его следует отклонить.
Поскольку для большего значения NPV не всегда соответствует большее значение PI, для оценки эффективности используют еще одну характеристику – внутреннюю скорость оборота для ряда последовательных периодических поступлений и выплат переменной величины (функция ВСД).
Функция ВСД вычисляет итеративным методом норму дисконтирования, при которой чистая текущая стоимость равна 0. Правило – чем выше величина ВСД тем больше эффективность инвестиции. Если известна рыночная норма дохода r, то вычисленное значение можно использовать в качестве оценки целесообразности принятия того или иного проекта вложения средств.
Проект принимается, если ВСД > r, и отвергается, если ВСД< r. Основанием для такого решения является то, что при ВСД < rожидаемых доходов от проекта оказывается недостаточно для покрытия всех финансовых платежей, и принятие такого проекта оказывается экономически нецелесообразным. Соответственно, при ВСД > rинвестор за счет доходов от проекта сможет не только выполнить все финансовые обязательства но и получить дополнительную прибыль. Такой проект экономически целесообразен и его следует принять.
Функция ВСД вычисляет внутреннюю скорость оборота инвестиции для ряда периодических выплат и поступлений переменной величины. Значение функции вычисляется из формулы (8) для NPV= 0:
 , (10) , (10)
где п – количество выплат и поступлений;
valuei – значения выплат и поступлений;
R – внутренняя скорость оборота.
Синтаксис: ВСД (значения;предположение).
Начиная со значения предположение, функция ВСД выполняет циклические вычисления, пока не получит результат с точностью 0,00001 %. Если функция ВСД не может получить результат после 20 попыток, то возвращается значение ошибки #ЧИСЛО!
В большинстве случаев нет необходимости задавать аргумент предположение для вычислений с помощью функции ВСД. По умолчанию аргумент предположение полагается равным 0,1 (10 %). Если ВСД выдает значение ошибки #ЧИСЛО! или если результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз с другим значением аргумента предположение.
Функция ВСД позволяет оценить предел безопасности, т. е. если ВСД = 20 %, а r = 10 % то предел безопасности равен 10 %.
ПРАКТИКУМ
Задача 1. Фирме требуется 500 000 руб. через два года. Определить, какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500 000 руб., если процентная ставка составляет 12 % годовых при полугодовом начислении процентов.
Алгоритм решения задачи
Для расчета суммы текущего вклада зададим исходные данные в виде таблицы, диапазон ячеек A3:B7. При вводе формулы в ячейку В10 вызовем функцию ПС и в полях ее панели укажем адреса требуемых параметров (рисунок 3). В результате вычислений получим отрицательное значение, так как указанную сумму фирме потребуется внести.
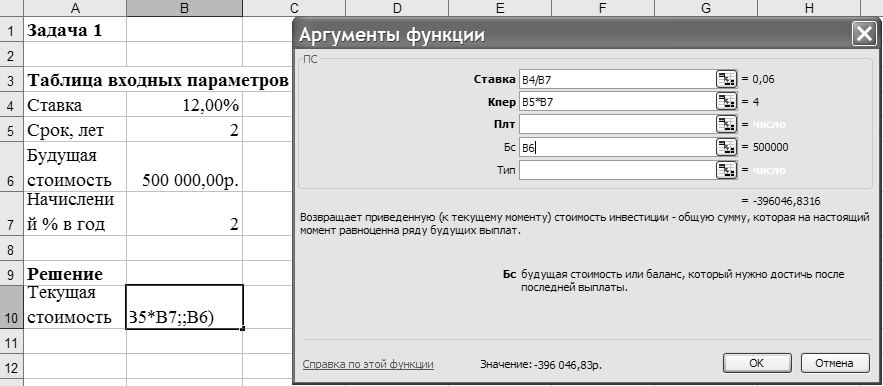
Рисунок –Фрагмент листа Excel с решением задачи о нахождении
текущей стоимости
Задача 2. Пусть инвестиции в проект к концу первого года его реализации составят 20 000 руб. В последующие четыре года ожидаются годовые доходы по проекту: 5 000 руб., 9 000 руб., 12 000 руб., 20 200 руб. Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 11 % годовых.
Алгоритм решения задачи
Иллюстрация решения задачи представлена на рисунке 4.
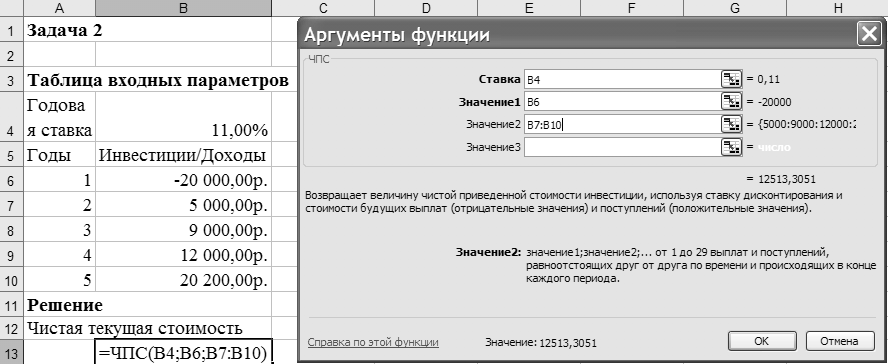
Рисунок –Фрагмент листа Excel с решением задачи о нахождении
чистой текущей стоимости
Чистая текущая стоимость проекта для периодических денежных потоков переменной величины рассчитывается с помощью функции ЧПС. Так как по условию задачи инвестиция в сумме 20 000 руб. вносится к концу первого периода, то это значение следует включить в список аргументов функции ЧПС со знаком «минус» (инвестиционный денежный поток движется «от нас»). Остальные денежные потоки представляют собой доходы, поэтому при вычислениях укажем их со знаком «плюс».
Задача 3. Определить внутреннюю ставку доходности проекта, если затраты по нему составят 100 млн руб., а ожидаемые в течение последующих четырех лет доходы будут: 40, 10, 20, 60 млн руб. Дать оценку проекта, если рыночная норма дохода составляет 11 %.
Алгоритм решения задачи
Внутренняя ставка доходности проекта рассчитывается с использованием функции ВСД. Подставив исходные данные в функцию, получим результат, представленный на рисунке 5.
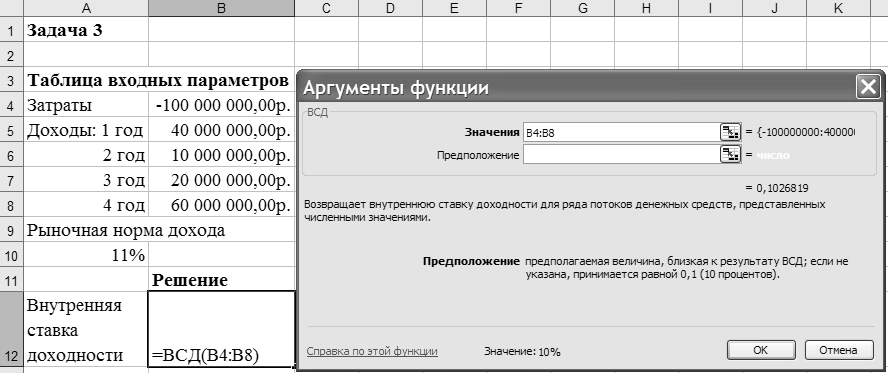
Рисунок –Фрагмент листа Excel с решением задачи о нахождении
внутренней ставки доходности
Вывод: проект следует считать невыгодным, поскольку в нашем случае внутренняя норма дохода 10,27 % меньше рыночной нормы дохода – 11 %.
|
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.