Цель работы: изучение функций Excel, предназначенных для финансовых расчетов по ценным бумагам.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
При расчетах по ценным бумагам с периодическими выплатами купонного дохода требуется определить длительность интервалов купонных выплат, а также их календарные даты.
Временной интервал купона разбивается на дни, предшествующие моменту приобретения ценной бумаги, и дни, следующие до очередной оплаты купона после приобретения ценной бумаги.
Функция ДНЕЙКУПОН вычисляет число дней в периоде купона для ценных бумаг.
Синтаксис: ДНЕЙКУПОН(дата_соглашения; дата_вступления_в_силу; периодичность; базис),
где дата_соглашения – дата приобретения ценной бумаги, дата инвестиций в ценные бумаги (более поздняя, чем дата выпуска); Дата соглашения не может превышать дату вступления в силу.
дата_вступления_в_силу – дата погашения ценной бумаги;
периодичность (частота) – задается как число, принимающее следующие значения в зависимости от количества выплат по купонам за год:
1 – один раз в год (ежегодная выплата);
2 – два раза в год (полугодовая выплата);
4 – четыре раза в год (ежеквартальная выплата).
Иных значений периодичности не допускается;
Аргумент базис не является обязательным, однако играет важную роль, по�скольку влияет на точность вычислений. В зависимости от способа вычисления временного периода аргумент базис может принимать следующие значения:
0 – US(NASD) – американский стандарт, согласно которому месяц равен 30, а год – 360 дням; принимается по умолчанию;
1 – фактический/фактический – фактическая длина месяца и года;
2 – фактический/360 – фактическая длина месяца, год равен 360 дням;
3 – фактический/365 – фактическая длина месяца, год равен 365 дням;
4 – европейский 30/360 – европейский стандарт, длина месяца равна 30 дням, длина года принимается 360 дней.
Замечания:
Все даты должны быть выражены в числовом формате. Для этих целей служит функция ДАТА (год; месяц; день), которая преобразует заданную дату в числовой формат или, если дата задана текстом, – функция ДАТАЗНАЧ (дата_как_текст). Кроме того, Excel предоставляет возможность автоматически преобразовывать дату в числовой формат, если в рассматриваемых функциях используется ссылка на ячейку, в которой содержится дата. Например, дату 3 января 2006 г. следует вводить в числовом формате как 38720.
Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона. Пусть, например, облигация со сроком действия 30 лет выпущена 1 января 2009 года и была приобретена покупателем через шесть месяцев после своего выпуска. Датой выпуска будет являться 1 января 2009 года, датой расчета – 1 июля 2009, а срок погашения такой облигации – 1 января 2039 года, то есть через 30 лет после даты выпуска.
Функция ЧИСЛКУПОН рассчитывает количество купонов, которые могут быть оплачены между датой соглашения (покупки) и датой вступления в силу (погашения) ценной бумаги, округленное до ближайшего целого количества купонов.
Синтаксис: ЧИСЛКУПОН(дата_соглашения; дата_вступления_в_силу; пе�риодичность; базис).
Число купонных выплат зависит от даты приобретения ценной бумаги и периодичности.
Функция ДАТАКУПОНДО вычисляет последнюю дату выплаты купона, предшествующую покупке (дате соглашения) ценной бумаги.
Синтаксис: ДАТАКУПОНДО(дата_соглашения; дата_вступления_в_ силу; периодичность; базис).
Функция ДНЕЙКУПОНДО определяет количество дней, прошедших от момента купонного платежа до даты соглашения (покупки) ценной бумаги:
Синтаксис: ДНЕЙКУПОНДО(дата_соглашения; дата_вступления_в_ силу; периодичность; базис).
За указанное время идет накопление купонного дохода, который влияет на цену покупки (курс) облигации.
Функция ДАТАКУПОНПОСЛЕ определяет дату оплаты купона, следующую за датой приобретения ценной бумаги.
Синтаксис: ДАТАКУПОНПОСЛЕ(дата_соглашения; дата_вступления_в _силу; периодичность; базис).
Функция ДНЕЙКУПОНПОСЛЕ рассчитывает число дней от момента приобретения ценной бумаги до оплаты очередного купона. За указанный срок осуществляется накопление купонного дохода, который будет выплачен владельцу облигации:
Синтаксис: ДНЕЙКУПОНПОСЛЕ(дата_соглашения; дата_вступления_в _силу; периодичность; базис).
При одинаковых параметрах ценных бумаг выполняется соотношение:
ДНЕЙКУПОН = ДНЕЙКУПОНДО + ДНЕЙКУПОНПОСЛЕ.
Функция ДОХОД позволяет рассчитать годовую ставку помещения по операциям с ценными бумагами при заданной купонной ставке и разности курсов покупки и погашения за указанный период действия ценной бумаги.
Синтаксис: ДОХОД(дата_соглашения; дата_вступления_в_силу; ставка; цена; погашение; частота; базис).
Дополнительными аргументами в этой функции являются:
ставка – годовая ставка выплат по купонам, в %;
цена – рыночная цена (в абсолютном выражении) или курс (в относительном выражении) ценной бумаги при покупке инвестором;
погашение – цена (в абсолютном выражении) или курс (в относительном выражении) продажи ценной бумаги инвестором.
Расчет ведется согласно формуле годовой ставки помещения. Функция учитывает, сколько периодов купонов укладывается до даты погашения, а также накопленный купонный доход от момента последней оплаты купона до даты приобретения (соглашения). Если ценная бумага имеет более одного оплачиваемого купона, то функция ДОХОД вычисляется итерационным методом (но не более 100 итераций), используя метод Ньютона на основе формулы для функции ЦЕНА. Доход изменяется до тех пор, пока вычисляемая цена для данного дохода не станет близкой к указанному значению аргумента цена.
С ростом купонной ставки годовая ставка дохода ценной бумаги растет, с увеличением курса покупки ценной бумаги – падает. Если курс покупки ценной бумаги равен 100, то годовая ставка помещения равна купонной ставке. При курсе ценной бумаги больше 100 (выше номинала) годовая ставка помещения меньше купонной ставки, при курсе ценной бумаги меньше 100 годовая ставка помещения выше купонной ставки. Отрицательное значение годовой ставки помещения означают нецелесообразность инвестиций.
Функция ЦЕНА рассчитывает курс (цену) покупки ценной бумаги с периодическими выплатами купонных процентов.
Синтаксис: ЦЕНА(дата_соглашения; дата_вступления_в_силу; ставка; доход; погашение; частота; базис).
ПРАКТИКУМ
Задача 1. Облигации выпущены на следующих условиях: дата приобретения облигации (дата_соглашения) – 6.09.12; дата окончания действия облигации (дата_вступл_в_силу) – 12.09.14; периодичность равна 2, базис – 1. Определить число дней в периоде купона
Алгоритм решения задачи
Введем аргументы функции в ячейки электронной таблицы: дату соглашения – в ячейку В1, дату вступления в силу – в ячейку В2, периодичность – в ячейку В3 и базис – в ячейку В4, тогда функция примет вид: ДНЕЙКУПОН(В1; В2; В3; В4) = 184.
Задача 2. По данным задачи 1 определить количество купонов, которые могут быть оплачены между датами покупки и погашения ценной бумаги.
Алгоритм решения задачи
Обращаясь к данным из указанных ячеек сформируем функцию: ЧИСЛКУПОН(В1; В2; В3; В4) = 5.
Над этими данными можно провести манипуляции, обращаясь и к таким функциям, как ДНЕЙКУПОНДО, ДНЕЙКУПОНПОСЛЕ, ДАТАКУПОНДО, ДАТАКУПОНПОСЛЕ.
Задача 3. Определить размер купонной ставки, если годовая ставка помещения составляет 15 %, облигации приобретены 6.09.12 по курсу 89, купоны выплачиваются с периодичностью раз в полугодие. Предполагаемая дата погашения облигации – 12.09.17 по курсу (погашение) 100. Базис = 1.
Алгоритм решения задачи
В ячейки В4:В10 введем исходные данные. Размер купонной ставки введем в произвольную ячейку (например, В11), в другую ячейку (например, А14) – формулу расчета ставки помещения и установим курсор в ячейку с формулой. Вид ячейки с формулой следующий: =ДОХОД(B5;B6;B11;B7;B8;B9;B10)
Далее выполните команду Данные → Работа с данными → Анализ «что-если» → Подбор параметра. В поле Значение нужно ввести 15 %, в поле Изменяя ячейку указать адрес ячейки, содержащей значение купонной ставки (В11), и нажать кнопку ОК.
Рисунок – Результат подбора параметра функции ДОХОД
Результат определения дохода с помощью средства EXCEL Подбор параметраприведен на рисунке 14.
В ячейке, содержащей значение купонной ставки (в данном случае – В11), будет находиться величина 11,8%. При нажатии кнопки ОК подобранное значение аргумента сохраняется
Задача 4. Облигации приобретены (дата_соглашения) 6.09.2012 года и будут погашены (дата _погашения) 12.09.2017 года. Размер купонной ставки (купон) – 9 % с выплатой раз в полугодие. Ожидаемая годовая ставка помещения (доход) – 12,57 %, номинал облигации (погашение) – 100, базис расчета – 1. Определить цену облигации.
Алгоритм решения задачи
Пример решения задачи приведен на рисунке 15.
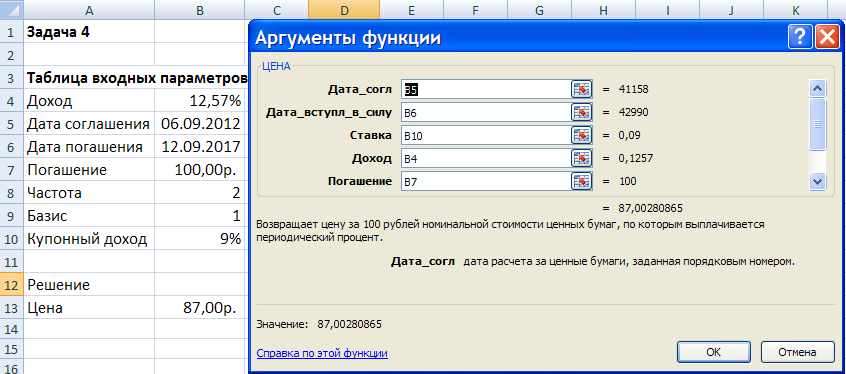
Рисунок – Пример использования функции ЦЕНА
С помощью команды Данные → Работа с данными → Анализ «что-если» → Подбор параметра решается обратная задача определения значения одного любого аргумента (ставка купонных выплат, доход, частота и др.) при заданном курсе (цене) ценной бумаги и сохранении значений прочих параметров. Поэтому целесообразно проверить решение задачи через функцию ДОХОД, а цену подобрать через Данные → Работа с данными → Анализ «что-если» → Подбор параметра, а задачи на функцию ДОХОД нужно проверять через функцию ЦЕНА, а доход подбирать через Данные → Работа с данными → Анализ «что-если» → Подбор параметра.
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.