ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
|
| Метод начисления процентов | Общее число периодов начисления процентов | Ставка процента за период начисления, % |
| Годовой | п | к |
| Полугодовой | п·2 | к/2 |
| Квартальный | п·4 | к/4 |
| Ежемесячный | п·12 | к/12 |
| Ежедневный | п·365 | к/365 |
Рассмотрим различные варианты использования функции БС при решении конкретных задач.
1. Допустим, необходимо рассчитать будущую стоимость единовременной суммы вклада, по которой начисляются сложные проценты определенное количество периодов. Эту величину можно рассчитать по формуле
где fv – будущая стоимость вклада или займа;
pv – текущая стоимость вклада (займа);
n – общее число периодов начисления процентов;
r – процентная ставка по вкладу (займу).
В этом случае на рабочем листе Excel формула примет вид: =БС(ставка;кпер;;пс;).
2. Рассмотрим ситуацию, когда платежи производятся систематически, а не один раз, как в предыдущем примере. Эти платежи могут осуществляться в начале каждого расчетного периода – обязательные платежи или платежи пренумерандо,в конце периода – обычные платежи или платежи постнумерандо в течение п периодов. Допустим, что в каждом периоде вносится одинаковая сумма. Требуется найти совокупную величину вложений, т. е. их будущую стоимость в конце п-го периода для обоих случаев. Отличие в расчете при этом заключается в том, что в каждом случае не происходит начисления процентов на последний вклад, т.е. все вклады пренумерандо увеличиваются на сложные проценты на один расчетный период больше, чем вклады постнумерандо.
Для расчета будущей стоимости пренумерандо используется формула
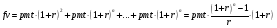 , (2)
, (2)где fv – будущая стоимость серии фиксированных платежей;
pmt – фиксированная периодическая сумма платежа;
п – общее число периодов выплат;
r – постоянная процентная ставка.
Этой формуле соответствует формула расчета наращенной суммы постоянной ренты пренумерандо. Тогда при расчете БС значение аргумента тип = 1 и формула примет вид =БС (ставка;кпер;плт;пс;1).
Результат должен совпадать с расчетом по формуле (2).
Для расчета будущей стоимости постнумерандо формула примет вид:

 . (3)
. (3)Соответствующая расчету по формуле (3) запись на рабочем листе Excel имеет вид: =БС(ставка;кпер;плт;пс;0).
Аргумент тип = 0 можно опустить и записать: =БС(ставка;кпер;плт;пс)
Если процентная ставка меняется с течением времени, то для расчета будущего значения инвестиции (единой суммы) после начисления сложных процентов можно использовать функцию БЗРАСПИС.
Синтаксис: БЗРАСПИС(инвестиция,{ставка1; ставка2; ...; ставкаN}).
Если применяется массив процентных ставок – {ставка1; ставка2; …ставкаN} , то ставки необходимо вводить не в виде процентов, а как числа, например, {0,1; 0,15; 0,05}. Но проще записать вместо массива ставок соответствующий интервал ячеек, содержащих значения переменных процентных ставок.
Функция БЗРАСПИС (FvSchedule) вычисляется по формуле:
FvSchedule = uнвестиция · (1+ставка1) · (1+ставка2) ·… · (1+cmaвкаN) (4).
ПРАКТИКУМ
Задача 1. На банковский счет под 11,5 % годовых внесли 37 000 руб. Определить размер вклада по истечении трех лет, если проценты начисляются каждые полгода.
Алгоритм решения задачи
Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем функцию БС (ставка; кпер; плт; пс; тип). Опишем способы задания аргументов данной функции.
В связи с тем, что проценты начисляются каждые полгода, аргумент ставка равен 11,5 % / 2. Общее число периодов начисления равно 3*2 (аргумент кпер). Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада), равный 37 000 руб., задается в виде отрицательной величины (-37000), поскольку для вкладчика – это отток его денежных средств (вложение средств). Если рассматривать решение данной задачи с точки зрения банка, то данный аргумент (пс) должен быть задан в виде положительной величины, т. к. означает поступление средств в банк.
Аргумент плт отсутствует, т. к. вклад не пополняется. Аргумент тип равен 0, т. к. в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Тогда к концу 3-го года на счете имеем (рисунок 1):
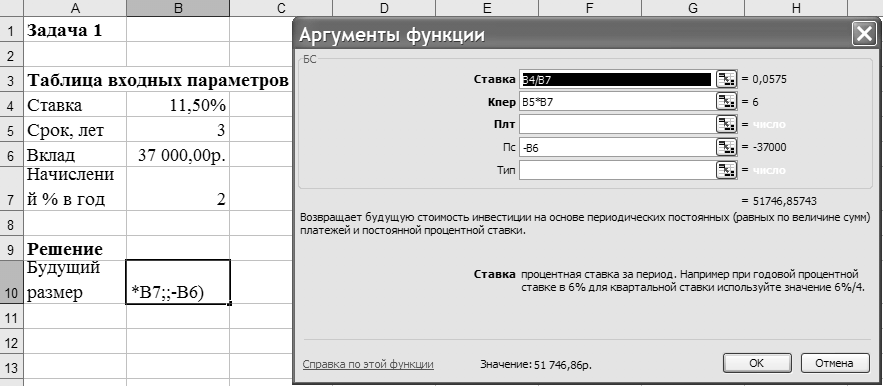
Рисунок –Фрагмент листа Excel с решением задачи о нахождении
будущего размера вклада
Задача 2. По облигации номиналом 100 тыс. руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10 %, в два последующих года – 20 %, в оставшиеся три года – 25 %. Рассчитаем будущую стоимость облигации по сложной процентной ставке.
Алгоритм решения задачи
Пусть в ячейки А1:А6 введены числа 10 %, 20 %, 20 %, 25 %, 25 %, 25 % соответственно, а в ячейку В1 – номинал облигации. Тогда наращенная стоимость облигации равна: =БЗРАСПИС(В1;А1:А6) = 309,38.
Задача 3. Исходя из плана начисления процентов, приведенного в задаче 2, рассчитаем номинал облигации, если известно, что ее будущая стоимость составила 1546,88 тыс. руб.
Алгоритм решения задачи
Для решения такой задачи необходимо использовать аппарат подбора параметра, вызываемый командой на ленте Данные → Работа с данными → Анализ «что-если» →Подбор параметра.

Рисунок – Диалоговое окно
Подбор параметра
Пусть в ячейки А1:А6 введен план начисления процентов. В ячейку В1 запишем формулу =БЗРАСПИС(В2; А1:А6). Так как ячейка В2 пустая, то в В1 окажется нулевое значение. Установив курсор в ячейку В1, выбираем команду Данные → Работа с данными → Анализ «что-если» →Подбор параметра и заполняем диалоговое окно следующим образом (рисунок 2). В результате в ячейке В2 появится значение номинала облигации – 500 тыс. руб.

