|
|
ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
Цель работы: освоение навыков применения функций Excel для расчета срока платежа и процентной ставки.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Функции этой группы позволяют находить величины, расчет которых весьма затруднен, если ведется вручную. К ним относятся:
общее число периодов постоянных выплат, необходимых для достижения заданного будущего значения; число периодов, через которое начальная сумма займа (вклада) достигает заданного значения (функция КПЕР);
значение постоянной процентной ставки за один период для серии фиксированных периодических платежей; значение ставки процента по вкладу или займу (функция СТАВКА).
Функция КПЕР вычисляет общее число периодов выплат, как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, найденное значение необходимо разделить на число расчетных периодов в году, чтобы найти число лет выплат.
Синтаксис: КПЕР(ставка;плт;пс;бс;тип).
Функция может применяться в следующих расчетах:
Если рассчитывается общее число периодов начисления процентов, необходимых для того, чтобы начальная сумма размером пс достигла указанного будущего значения бс, то формула примет вид: =КПЕР(ставка;;пс;бс;). В этом случае вычисляетcя п из формулы (1), выполнив преобразования и прологарифмировав обе части уравнения:
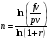 . (11) . (11)
Если эти платежи производятся в начале каждого расчетного периода, то соответствующий расчет в Excel имеет вид: =КПЕР(ставка;плт; ;бс; 1). Если платежи производятся в конце каждого периода, то формула примет вид: =КПЕР(став-ка;плт;;бс;).
При погашении займа размером пс равномерными постоянными платежами в конце каждого расчетного периода число периодов, через которое произойдет полное погашение, равно: =КПЕР(ставка;плт;пс;;).
Полученное значение можно также использовать как показатель срока окупаемости при анализе инвестиционного проекта. При этом предполагается, что поступление доходов происходит периодически равными величинами в конце или в начале каждого расчетного периода. Рассчитанное значение будет представлять число расчетных периодов, через которое сумма доходов, дисконтированных на момент завершения инвестиций, будет равна величине инвестиций.
Функция СТАВКА определяет значение процентной ставки за один расчетный период. Для нахождения годовой процентной ставки полученное значение следует умножить на число расчетных периодов, составляющих год.
Синтаксис: СТАВКА(кпер;плт;пс;бс;тип;предположение).
Функция СТАВКА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО! В этом случае можно попытаться задать другой аргумент предположение, по умолчанию равный 10 %. В большинстве случаев не требуется задавать аргумент предположение.
Рассмотрим три варианта практического применения этой функции:
Допустим, необходимо рассчитать процентную ставку по формуле (1) при известной текущей стоимости пс, будущей стоимости бс, числе периодов кпер. В этом случае формула в Excel в общем виде записывается так:
СТАВКА(кпер;;пс;бс;;предположение).
При расчетах по фиксированным обязательным или обычным периодическим платежам процентная ставка за расчетный период в Excel вычисляется так: СТАВКА(кпер;плт;;бс;тип;предположение).
Расчет процентной ставки по займу размером пс при равномерном погашении обычными периодическими платежами, при условии, что заем полностью погашается, ведется так: СТАВКА(кпер;плт;пс;;; предположение).
ПРАКТИКУМ
Задача 1. Рассчитать, через сколько лет вклад 10 000 руб. достигнет размера 100 000 руб., если годовая процентная ставка по нему – 13 % годовых и начисление процентов производится ежеквартально.
Алгоритм решения задачи
При квартальном начислении процентов ставка процента за период начисления равна 13 % / 4. Чтобы определить общее число периодов выплат для единой суммы вклада, воспользуемся функцией КПЕР со следующими аргументами: ставка = 13 % / 4; пс = -10 000; бс = 100 000.
Значением функции КПЕР является число периодов, необходимое для проведения операции, в данном случае – число кварталов. Для нахождения числа лет в ячейке В11 полученный результат разделим на 4.
Иллюстрация решения задачи приведена на рисунке 6.
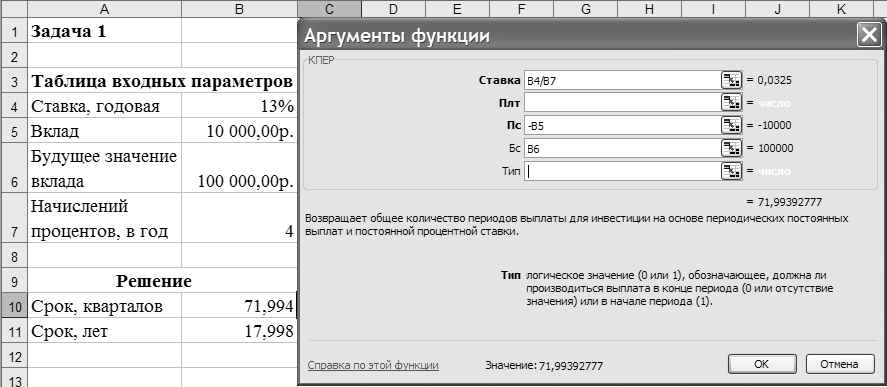
Рисунок –Иллюстрация применения функции КПЕР
Задача 2. Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Сумма разового платежа – 16 000 руб. На поступившие взносы начисляются 11,2 % годовых. Определить, когда величина фонда будет равна 100 000 руб.
Алгоритм решения задачи
Для определения общего числа периодов, через которое будет достигнута нужная сумма, воспользуемся функцией КПЕР с аргументами: ставка = 11,2 %; плт = -16 000; бс = 100 000. Если ставка занесена в ячейку В3, платеж – в ячейку В4 и фонд – в ячейку В5, то в результате вычислений получим, что через пять лет величина фонда достигнет отметки 100 000 руб.:
=КПЕР(B3;-B4;;B5)=5.
Задача 3. Предположим, что для получения через два года суммы в 1 млн. руб. предприятие готово вложить 250 тыс. руб. сразу и затем каждый месяц по 25 тыс. руб. Определить годовую процентную ставку.
Алгоритм решения задачи
В данной задаче сумма в 1 млн. руб. формируется за счет приведения к будущему моменту времени начального вклада 250 тыс. руб. и фиксированных ежемесячных выплат. В ячейке В11 определим значение процентной ставки за месяц с помощью функции СТАВКА, имеющей аргументы: Кпер = 2 · 12 = 24 (месяца); Плт = -25 000; Пс = -250 000; Бс – 1 000 000. Иллюстрация применения функции СТАВКА приведена на рисунке 7. Для вычисления годовой процентной ставки значение, выданное функцией СТАВКА, следует умножить на 12: 1,05 % · 12 = 12,63 %. Процент на вклад должен быть не меньше этой величины.
Обратим внимание, что функция СТАВКА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Сначала рассчитывается текущий объем инвестиции при ставке, задаваемой аргументом функции СТАВКА предположение, по умолчанию равным 10 %. Если результат получается больше 0, то значение процентной ставки увеличивается, и расчет текущего объема инвестиции повторяется. Если результат оказывается меньше 0, то для следующего приближения значение процентной ставки уменьшается. Процесс завершается, когда решение получится с точностью до 0,0000001 или когда количество итераций превысит 20. В последнем случае считается, что решения нет (формируется ошибка #ЧИСЛО!), и для повторного поиска решения следует изменить значение аргумента предположение. Это можно сделать, добавив его значение из интервала между 0 и 1 в строке формул или, сдвинув ползунок в панели функции СТАВКА, в появившейся строке ввести новое значение аргумента предположение.
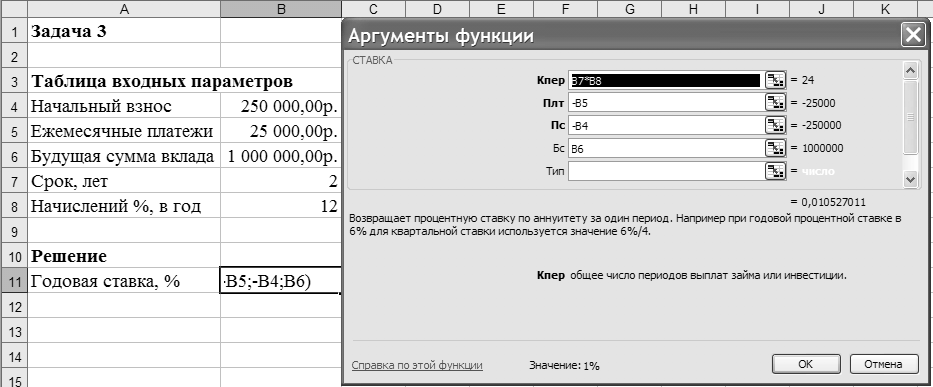
Рисунок – Фрагмент экрана при использовании функции СТАВКА
|
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.