|
|
ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
ЛАБОРАТОРНАЯ РАБОТА № 4
Расчет периодических платежей, анализ чувствительности
Цель работы: изучение функций Excel, предназначенных для расчета платежей, решение задач с помощью Таблицы подстановки.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Функции Excel позволяют вычислять следующие величины, связанные с периодическими выплатами.
Периодические платежи, осуществляемые на основе постоянной процентной ставки и не меняющиеся за все время расчета (функция ПЛТ).
Платежи по процентам за конкретный период (функция ПРПЛТ).
Основные платежи по займу (за вычетом процентов) за конкретный период (функция ОСПЛТ).
Все эти величины вычисляются, например, при расчете схемы равномерного погашения займа. Допустим, что заем погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость этих платежей будет равна сумме займа с начисленными процентами, к концу последнего расчетного периода, если в нем предполагается полное погашение займа.
С другой стороны, текущая стоимость выплат по займу должна равняться настоящей сумме займа. Если известна сумма займа, ставка процента, срок, на который выдан заем, то можно рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа с помощью функции ПЛТ. Функция ПЛТ вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставки.
Вычисленные платежи включают в себя сумму процентов по непогашенной части займа и основную выплату по займу. Обе величины зависят от номера периода и могут быть рассчитаны при помощи функций ПРПЛТ, ОСПЛТ.
Синтаксис: ПЛТ(ставка;кпер;пс;бс;тип).
Функция ПЛТ применяется в следующих расчетах:
1. Допустим, известна будущая стоимость фиксированных периодических выплат, производимых в начале или в конце каждого расчетного периода. Требуется рассчитать размер этих выплат. Для этого можно использовать формулы (2) и (3) (аргумент pmt). Соответствующая запись в Excel имеет вид: ПЛТ(ставка;кпер;;бс;тип).
2. Предположим, рассчитываются равные периодические платежи по займу величиной пс, необходимые для полного погашения этого займа через кпер периодов. Текущая стоимость этих выплат должна равняться текущей сумме займа, поэтому для расчета можно использовать формулу (1), выразив из нее аргумент pmtчерез текущую сумму займа, ставку процента и число периодов. Соответствующий расчет в Excel выполняется по формуле: ПЛТ(ставка;кпер; пс;;тип). Обычно погашение происходит в конце каждого расчетного периода. Для этого случая формула имеет вид: ПЛТ(ставка;кпер;пс;;), так как аргумент тип = 0.
Если заем погашается не полностью, т. е. его будущее значение не равно 0, то следует указать аргумент бс, который будет равен непогашенному остатку займа после всех выплат.
Функция ПРПЛТ. вычисляет платежи по процентам за заданный период на основе периодических постоянных выплат и постоянной процентной ставки. Синтаксис: ПРПЛТ(ставка;период;кпер;пс;бс;тип).
Функция предназначена для следующих расчетов:
При равномерном погашении займа постоянная периодическая выплата включает в себя платежи по процентам по непогашенной части займа и выплату задолженности. Так как непогашенная часть займа уменьшается по мере его погашения, то уменьшается и доля платежей по процентам в общей сумме выплаты и увеличивается доля выплаты задолженности. Чтобы найти размер платежа по процентам на конкретный период, следует использовать формулу: ПРПЛТ(ставка;период;кпер;пс;;), если погашение займа производится равными платежами в конце каждого расчетного периода.
Допустим, необходимо вычислить доход, который приносят постоянные периодические выплаты за конкретный период. Этот доход представляет собой сумму процентов, начисленных на накопленную (с процентами) к данному моменту совокупную величину вложений. Расчет ведется по формуле ПРПЛТ(ставка;период;кпер;;бс;тип).
Функция ОСПЛТ. вычисляет величину основного платежа (выплаты задолженности) по займу, который погашается равными платежами в конце или начале каждого расчетного периода, на указанный период.
Синтаксис: ОСПЛТ(ставка;период;кпер;пс;бс;тип).
ПРАКТИКУМ
Задача 1. Клиенту банка необходимо накопить 200 тыс. руб. за два года. Он обязуется вносить в начале каждого месяца постоянную сумму под 10 % годовых. Какой должна быть эта сумма?
Алгоритм решения задачи
Для определения ежемесячных выплат применяется функция ПЛТ с аргументами: Ставка = 10 % / 12 (ставка процента за месяц); Кпер = 2 * 12 = 24 (общее число месяцев начисления процентов); Бс = 200 000 (будущая стоимость вклада); Тип – 1, так как вклады пренумерандо. Иллюстрация решения задачи приведена на рисунке 8.
Результат со знаком «минус», так как 7 499,82 руб. клиент ежемесячно вносит в банк
=ПЛТ(В6/В8;В4*В8;;В5;В7)
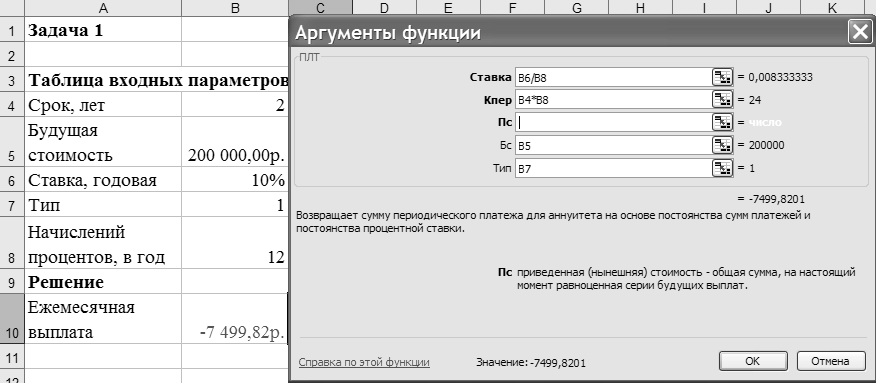
Рисунок – Иллюстрация применения функции ПЛТ
Задача 2. Определить платежи по процентам за первый месяц от трехгодичного займа в 100 000 руб. из расчета 8 % годовых.
Алгоритм решения задачи
Для определения платежа по процентам за первый месяц заданного периода применим функцию ПРПЛТ со следующими аргументами: Ставка = 8 % / 12 (процентная ставка за месяц); Период = 1 (месяц); Кпер= 3 · 12 = 36 (месяцев), Пс =100 000 (величина займа). Тогда платежи по процентам за первый месяц составят, как показано на рисунке 9, -666,67 руб.
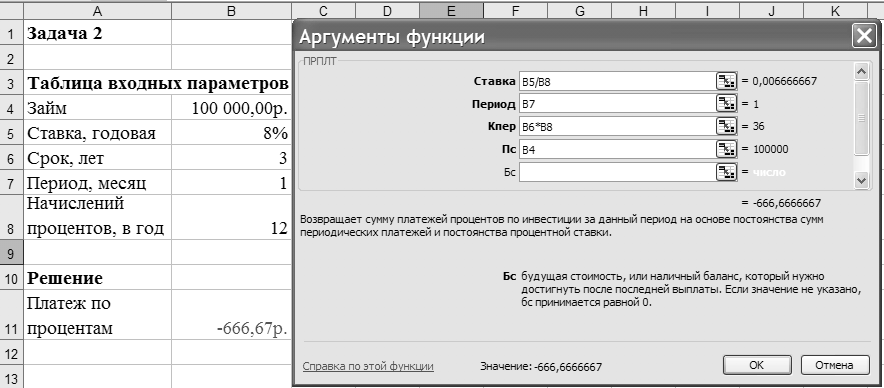
Рисунок – Фрагмент окна с использованием функции ПРПЛТ
Знак «минус» означает, что платеж по процентам необходимо внести.
Задача 3. Определить значение основного платежа для первого месяца двухгодичного займа в 60 000 руб. под 12 % годовых.
Алгоритм решения задачи
Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ. Иллюстрация решения показана на рисунке 10, в ячейке В11 показан результат вычислений.
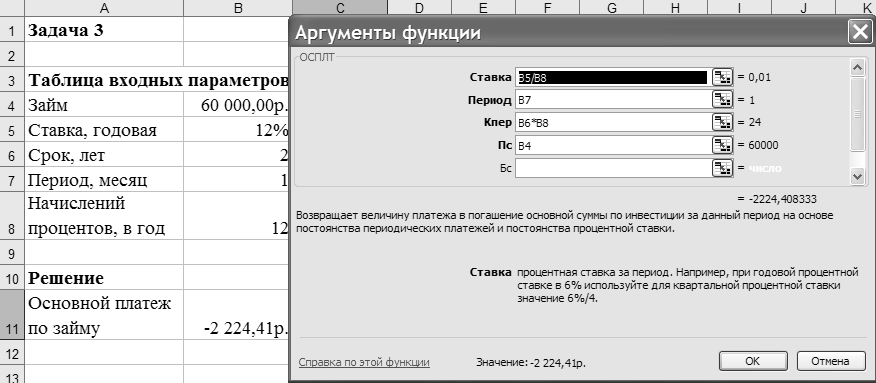
Рисунок – Фрагмент окна с использованием функции ОСПЛТ
Знак «минус» в результате означает, что сумму основного долга по займу необходимо внести.
Отметим, что сумма выплаты по процентам, вычисляемая с помощью функции ПРПЛТ, и сумма основной выплаты за период, рассчитанная с помощью функции ОСПЛТ, равны полной величине выплаты, вычисляемой с помощью функции ПЛТ.
Задача 4. Составить схему погашения займа в 70 000 руб., выданного сроком на 3 года под 17 % годовых, рассчитанную с помощью финансовых функций Excel.
Алгоритм решения задачи
Схема погашения займа будет включать все финансовые функции рассмотренные в данной лабораторной работе. Схема погашения займа представлена на рисунке 11.
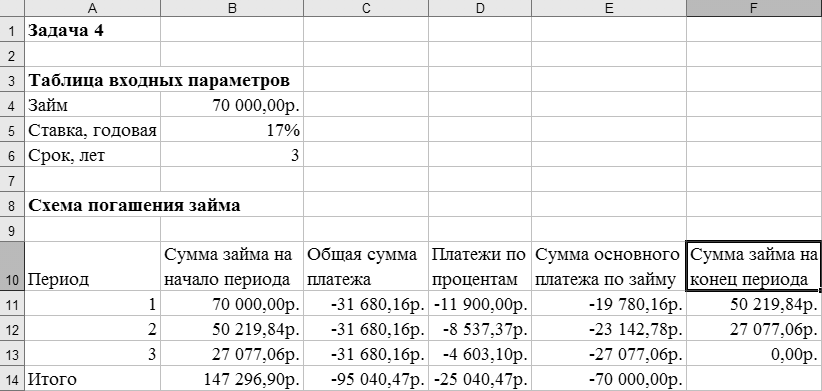
Рисунок – Схема погашения займа
При составлении схемы погашения займа особое внимание следует уделять формированию функций в первой строке таблицы (строка № 11), чтобы не произошло искажение функций при копировании их в другие строки таблицы. В ячейке С11 функция постоянного платежа должна выглядеть следующим образом: ПЛТ($B$5;$B$6;$B$4). Все аргументы функции заключены в абсолютные адреса ячеек, т. к величина постоянного платежа должна сохраниться неизменной на всем протяжении срока погашения займа. Функция платежей по процентам в ячейке D11 должна быть записана также с учетом абсолютных адресов ячеек, за исключением аргумента период, ее вид будет следующим: ПРПЛТ($B$5;А11;$B$6;$B$4). Аналогичным образом будет записана функция основных платежей в ячейке Е11: ОСПЛТ($B$5;А11;$B$6;$B$4). В ячейке F11 рассчитывается сумма займа на конец периода как разность между суммой займа на начало периода и основным платежом по займу. После расчета первой строки таблицы блок ячеек C11:F11 скопировать вниз на столько строк, сколько периодов в сроке погашения займа (в нашем примере строки № 12 и 13). После чего значение суммы займа на конец периода, полученное в ячейке F11, записать в ячейку В12, строка № 12 автоматически пересчитается, затем значение из ячейки F12 записать в ячейку В13, строка № 13 автоматически пересчитается. Если расчет выполнен правильно, то сумма займа на конец последнего периода будет равна 0, а итоговая сумма основного платежа будет равна сумме займа.
Задача 5 (анализ чувствительности). Для покупки недвижимости инвестор взял в банке кредит в сумме 12 млн. руб. Определить ежемесячные выплаты по кредиту для разных процентных ставок и сроков погашения кредита.
Алгоритм решения задачи
Ежемесячные выплаты по займу рассчитываются с использованием функции ПЛТ. Однако аргументы данной функции – процентная ставка и срок погашения кредита – по условию могут принимать различные значения. Поэтому рассмотрим влияние этих параметров на заданную функцию. Воспользуемся механизмом Таблица данных, который находится на ленте Данные → Работа с данными →Анализ «что-если». Выполним следующую последовательность действий.
В ячейку электронного листа СЗ введем числовое значение суммы кредита (12 000 000).
В ячейки С4, С5 введем произвольные (условные) значения процентной ставки (например, 5 %), и срока погашения кредита в годах (например, 1), которые нам понадобятся при построении Таблицы данных. В ячейку С6 введем количество выплат в году – 12.
В ячейки А9:А15 введем различные значения процентных ставок. В ячейки В8:Н8 – возможные сроки погашения.
В ячейку А8 введем формулу для расчета ежемесячных выплат по займу на основе данных таблицы подстановки: = ПЛТ(С4 / С6; С5 * С6; С3).
Выделим интервал для таблицы данных, включающий формулу и все исходные данные, – А8:Н15.
Выполним Данные → Работа с данными →Анализ «что-если» → Таблицы данных. В появившемся диалоговом окне (рисунок 12) заполним соответствующие поля. Поскольку наша таблица зависит от двух параметров, то в поле Подставлять значения по столбцам в: введем ссылку на ячейку С5 (срок погашения), а в поле Подставлять значения по строкам в: – ссылку на ячейку С4 (ставка).
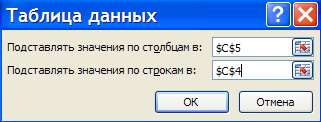
Рисунок – Окно задания
параметров таблицы постановки
Подтвердим ввод нажатием клавиши ‹Enter› или кнопкой ОК.
Таблица ежемесячных выплат по кредиту с помощью таблицы подстановки будет сформирована (рисунок 13).
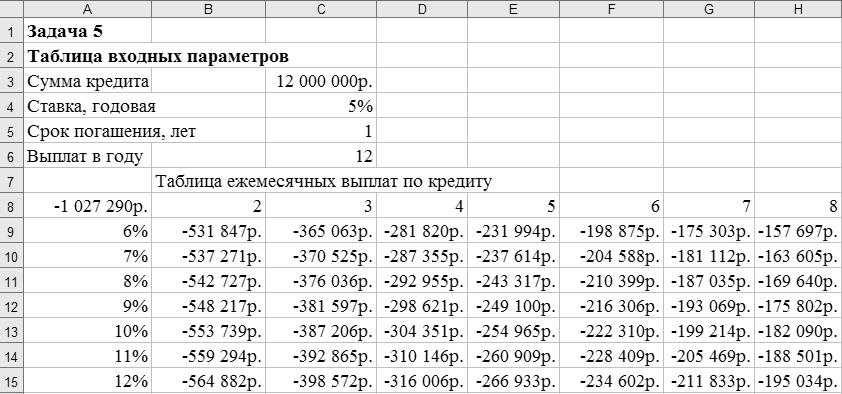
Рисунок – Фрагмент окна с таблицей ежемесячных выплат по кредиту
|
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.