ФИНАНСОВЫЕ ФУНКЦИИ лаб работы. Лабораторная работа 1 Определение будущей стоимости на основе постоянной и переменной процентной ставки Цель работы
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
|
Транспортная задача. Менеджмент электролампового объединения должен решить проблему снабжения четырех заводов комплектующими, производимых в трех цехах объединения: цех1 – стеклом, цех2 – цоколями, цех3 – спиралью. Потребности в комплектующих каждого из заводов соответственно равны 120, 50, 190 и 110 ед. ежедневно. Запасы комплектующих, вывозимых из цехов, соответственно равны 160, 140, 170 ед. На каждый из заводов комплектующие могут завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются в таблице 12. Таблица 12 – Исходные данные задачи
Алгоритм решения задачи Цель принятия решения – минимизация транспортных затрат при перевозках комплектующих из цехов на заводы. Требуется принять решение по объемам отгружаемых комплектующих из цехов по каждому заводу, с учетом цели решения. Постановка задачи
7х11 + 8х12 + х13 + 2х14 + 4х21 + 5х22 + 9х23 + 8х24 + 9х31 + 2х32 + 3х33 + 6х34 → min. 4. Сформулируем ограничения для задачи: • по вывозимому стеклу, цоколям, спирали из цехов, ед.: х11+ х12+ х13+ х14≤160; х21 + х22 + х23 + х24 ≤ 140; х31 + х32 + х33 + х34 ≤ 170; • по потребности заводов в комплектующих, ед.: х11+x21+ х31 ≥ 120; х12+ х22 + х32≥ 50; х13 + х23 + х33 ≥ 190; х14 + х24 + х34≥ 110; • областные ограничения: х11, х21,…,х34 ≥ 0 Решение задачи Создать таблицу с исходными данными, для чего:
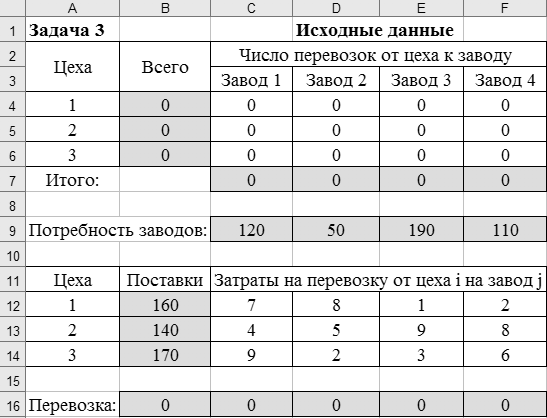 Рисунок 49 – Пример формирования модели для задачи 3 На основании исход ных данных (см. таблицу 12) построим математическую модель для решения задачи на листе электронной таблицы. Модель решения задачи показана на рисунке 49.  Рисунок 50 – Диалоговое окно Поиск решения для решения транспортной задачи Для решения задачи и нахождения оптимального плана перевозок используем процедуру Поиск решения (рисунок 50). Введем ячейку с целевой функцией, изменяемые ячейки, ограничения, в поле Равной установим минимальное значение целевой функции. Нажав на клавишу Параметры, выберем Линейную модель, нажмем ОКи Выполнить. Результат оптимизации показан в таблице на рисунке 51. Таким образом, математическая постановка данной транспортной задачи состоит в нахождении такого неотрицательного ре шения системы линейных уравнений, при котором целевая функция принимает минимальное значение. 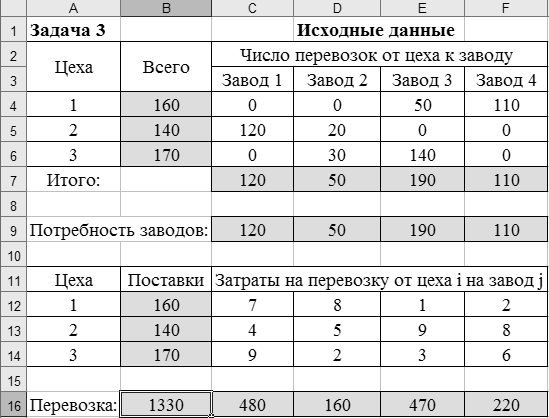 Рисунок 51 – Результаты решения задачи 3 ЛАБОРАТОРНАЯ РАБОТА № 12 Корреляционно-регрессионный анализ с использованием Excel Цель работы: изучить возможности табличного процессора Excel для проведения корреляционно-регрессионного анализа. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Корреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков. Он применяется в том случае, когда данные наблюдений можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону. Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и в определении на ее основе оценок частных и множественных коэффициентов корреляции и детерминации. Дополнительная задача корреляционного анализа (являющаяся основной в регрессионном анализе) - оценка вида уравнения связи (регрессии). Коэффициенты корреляции обычно представляются в матричной форме: 1 r12 … r1p r21 1 ... r2p . . . . . . rp1 rp2 … 1 Так как матрицы симметричны, иногда печатаются только их диагональные и над или поддиагональные элементы. Коэффициент корреляции используется для определения наличия взаимосвязи и ее количественной оценки двух наборов данных. Например, можно установить зависимость между величиной складского товарооборота и размером складской площади. Коэффициент корреляции выборки представляет собой ковариацию двух наборов данных, деленную на произведение их стандартных отклонений. Уравнение для коэффициента корреляции имеет следующий вид: 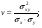 (23) (23) (24) (24)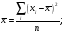 (25) (25)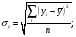 (26) (26)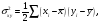 (27) (27)где х и у – значения изучаемых признаков; п – количество значений х и у в выборке; σх и σу – средние квадратичные отклонения;  и и 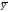 – средние величины по каждому признаку; – средние величины по каждому признаку;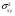 – межгрупповая дисперсия результативного признака по фактическому. – межгрупповая дисперсия результативного признака по фактическому.Для характеристики изменчивости признаков используют следующие показатели: вариационный размах, среднеквадратическое отклонение и коэффициент вариации. Вариационный размах (амплитуда колебания) – разница между максимальным и минимальным значениями изучаемого признака. Размах дает представление о крайних пределах вариации признаков, но не показывает степени изменчивости. Среднее квадратичное отклонение (б) характеризует степень изменчивости признака в абсолютных величинах. В нормальных или близких к ним вариационных рядах отклонение вправо и влево от средней (х) относятся на три сигмы (3σ). По этому показателю средней изменчивости можно ориентировочно определить минимальное и максимальное значения х. Коэффициент вариации характеризует изменчивость признака в изучаемой совокупности в относительных величинах. Его исчисляют как процентное отношение среднего квадратичного отклонения изучаемой совокупности к средней арифметической. Изменчивость признака считается незначительной, когда коэффициент вариации не более 10 %, средней – от 11 до 30 %, высокой – свыше 30 %. Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или, наоборот, малые значения одного набора связаны с большими значениями другого набора (отрицательная корреляция), или данные двух диапазонов никак не связаны (корреляция близка к нулю). Для вычисления коэффициента корреляции между двумя наборами данных используется статистическая функция КОРРЕЛ (находится в категории Статистические). Функция КОРРЕЛ рассчитывает коэффициент корреляции между диапазонами или массивами ячеек. Синтаксис: КОРРЕЛ(массив1;массив2), где массив1(fx)– это первый интервал ячеек со значениями; массив2(fx) – это второй интервал ячеек со значениями. Аргументами функции могут быть числа, имена, массивы или ссылки, содержащие числа. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются. Однако ячейки с нулевыми значениями учитываются. Если массив1 и массив2 имеют различное количество точек данных; (разное количество ячеек), то функция КОРРЕЛ объявляет значение ошибки #Н/Д. Если массив1 и массив2 пусты или стандартное отклонение (s)их значений равно нулю, то функция КОРРЕЛ указывает значение ошибки #ДЕЛ/0! Корреляционные связи различают:
Для измерения тесноты связи между результатом и признаками используют коэффициенты линейной и множественной корреляции, а также коэффициент регрессии. Коэффициент линейной корреляции – показатель, отображающий направление и тесноту связи между признаками при прямолинейных (или близких к ним) взаимозависимостях. Он колеблется в пределах от 0 до ±1. Знак «+» означает прямую, а знак «-» – обратную связь. Значения коэффициента линейной корреляции и теснота связи между признаками указаны в таблице 13. Таблица 13 – Значение коэффициента корреляции
Теснота связи двух или более признаков выражается коэффициентом множественной корреляции (совокупной). В случае линейной зависимости (у) от двух признаков (х и z) коэффициент корреляции вычисляют по формуле:  (28) (28)где ryx,ryz, rxz– коэффициенты корреляции между парами признаков. Коэффициент множественной корреляции – число всегда положительное и изменяется от 0 до 1. Для его исчисления предварительно вычисляют частные коэффициенты корреляции. Во многих практических задачах, исследующих различного рода зависимости необходимо на основании экспериментальных данных выразить зависимую переменную в виде некоторой математической функции от независимых переменных, т. е. построить регрессионную модель. Регрессионный анализ – это статистический метод исследования зависимости случайной величины Y от переменных Xj (j = l, 2,.... k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения Xj. Наиболее часто встречаются линейные уравнения регрессии вида: Y=βo+β1Xi1+β2Xi2+...+βkXik+εi Коэффициент регрессии βi, показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу его измерения, т. е. является нормативным коэффициентом. Коэффициент регрессии исчисляется по формулам: 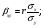 (29) (29) (30) (30)Коэффициент регрессии имеет два значения и включает коэффициент корреляции (r)и среднеквадратическое отклонение по обоим признакам (σхи σy). Он может быть положительным и отрицательным в зависимости от значения коэффициента корреляции. Если Y есть функция только одной переменной X, независимо от того, линейная ли или нелинейная зависимость между У и Х, то имеет место двумерный статистический анализ. Если же Y является функцией более чем одного фактора X (X1, X2, …, Xk), то связь множественная, и для исследования вида связи и ее оценки, применяются методы множественной регрессии и корреляции. Регрессионный анализ для линейных зависимостей в Excel можно проводить также, используя статистическую функцию ЛИНЕЙН, которая рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имею щиеся данные. Функция возвращает массив, который описывает прямую. Синтаксис: ЛИНЕЙН(известные_значения_у; известные_значения_ х; конст; статистика) где известные_значения_у – множество значений у, которые уже известны для соотношения y = mx + b (уравнение прямой): • если массив известные_значения_у имеет 1 столбец, тo каждый столбец массива известные_значения_х интерпретируется как отдельная переменная; • если массив известные_значения_у имеет одну строку, то каждая строка массива известные_значения_х интерпретируется как отдельная переменная; известные_значения_х – это необязательное множество значений х, которые уже известны для соотношения y = mx + b; массив известные_значения_х может содержать одно или несколько множеств переменных: • если используется только одна переменная, то известные_значения_у и известные _значения_х могут быть массивами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные _значения_у должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец). • если параметр известные_значения_х опущен, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и параметр известные _значения_у; конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна нулю: • если параметр конст имеет значение ИСТИНА или опущен, то b вычисляется обычным образом; • если конст имеет значение ЛОЖЬ; то b полагается равным нулю и значения m подбираются так, чтобы выполнялось соотношение у = mx; статистика – логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. • если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику; • если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b. ПРАКТИКУМ Задача 1. Необходимо выяснить, имеется ли взаимосвязь показателей эффективности производства продукции на машиностроительных предприятиях в целом по группе однотипных производств. В качестве показателей оценки эффективности были выбраны следующие факторы: производительность труда, фондоотдача, материалоемкость продукции. Статистическая информация о динамике и значениях этих показателей была собрана по отрасли машиностроения, из которой в качестве статистической выборки была отобрана для анализа группа из 25 однотипных машиностроительных предприятий. На основании исследования годовых отчетов предприятий были получены следующие данные (таблица 14): х – выработка валовой продукции в неизменных ценах на одного работающего средней списочной численности ППП, млн. руб.; у – выпуск валовой продукции на 1 руб. среднегодовой стоимости основных промышленно-производственных фондов, руб.; z – материалоемкость в стоимостном выражении: стоимость материалов в валовой продукции в неизменных ценах, %. Таблица 14 – Исходные данные к задаче
Алгоритм решения задачи 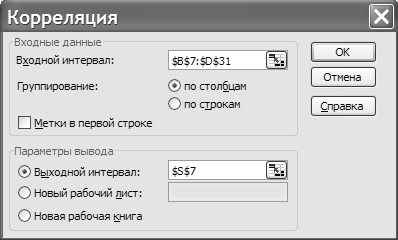 Рисунок 52 – Диалоговое окно Корреляция Итоговую таблицу, где будем формировать решение задачи, разместим в ячейках диапазона А6 : D31. Для проведения корреляционного анализа используем модуль Анализ данных на ленте Данные → Анализ, в котором необходимо активизировать инструмент анализа Корреляция. При этом откроется диалоговое окно Корреляция (рисунок 52), в котором необходимо заполнить предлагаемые поля. Порядок заполнения может быть следующим. 1. Входной диапазон. Вводится ссылка на диапазон ячеек $B$7:SD$31, содержащие анализируемые данные. Примечание. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк. 2. Выходной диапазон. Вводится ссылка на левую верхнюю ячейку выходного диапазона $S$7. Примечание. Поскольку коэффициент корреляции двух наборов данных не зависит от последовательности их обработки, то выходная область занимает только половину предназначенного для нее места. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, т. к. каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой. 3. Группирование. Для этого необходимо установить переключатель в положение по столбцам и нажать ОК. В блок ячеек S7:V10 вставляется корреляционная матрица с выходными данными: Из полученных расчетов видно, что поддиагональные элементы пред ставляют собой не что иное, как парные коэффициенты корреляции: rxy, rxz, ryz. Для проверки корреляционного анализа воспользуемся статистической функцией КОРРЕЛ, для чего введем в ячейки формулы:  Рисунок 53 – Результаты решения задачи 1 V12: =КОРРЕЛ(В7:В31; С7:С31); V13: =КОРРЕЛ(В7:В31; D7:D31); V14: =КОРРЕЛ(С7:С31; D7:D31). Расчетные коэффициенты приведены в ячейках V12:V14. На рисунке 53 показан расчет выходных данных, представленных в виде корреляционной матрицы и коэффициентов корреляции, полученных с помощью функции КОРРЕЛ. Вывод: доказана тесная (очень высокая) взаимосвязь каждого из исследуемых показателей эффективности работы предприятия с другими. Необходимо учитывать что при построении многофакторных корреляционных моделей, одной из предпосылок обоснованности конечных результатов, является требование возможно меньшей зависимости между факторами (отсутствие мультиколлинеарности) Если величина парного коэффициента учитывающего степень тесноты связи между двумя факторными признаками по абсолютной величине 0,87 и более то такие факторы считаются коллинеарными. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
Поэтому при построении модели следует исключать один из каждой пары факторных признаков, коэффициент корреляции между которыми превышает 0,87 и проделать корреляционный анализ еще раз. Задача 2. Для предприятий, производящих строительные материалы, на основе регрессионной модели провести исследование наличия и вида зависимости такого экономического показателя деятельности, как фондоотдача в процентах на единицу ОПФ (у) от среднечасовой производительности вращающихся печей (х1) и удельного веса активной части ОПФ (х2). Исходные данные для цементных заводов, отобранные в качестве генеральной совокупности, приводятся в таблице 15 (n= 15). Таблица 15 – Исходные данные
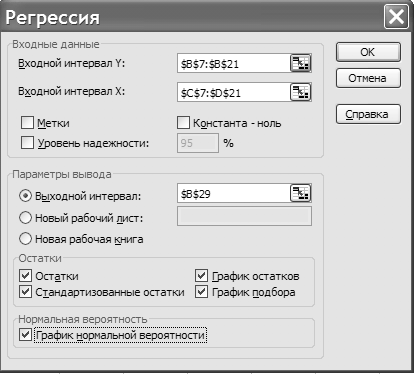 Рисунок 54 – Диалоговое окно Регрессия Алгоритм решения задачи В блок ячеек A6:D21 поместить таблицу с исходными данными. Для решения задач регрессионного анализа используем модуль – Анализ данных на ленте Данные → Анализ. Его активизация открывает диалоговое окно Анализ данных, в котором следует выбрать инструмент Регрессия, на экране появится диалоговое окно определения параметров Регрессия (рисунок 54). В поле Входной интервал Y вводится ссылка на диапазон анализируемых зависимых данных ($В$7: $В$21). Диапазон должен состоять из одного столбца. В поле Входной интервал Х делается ссылка на диапазон независимых данных,подлежащих анализу (блок ячеек $C$7:$D$21). Диапазон независимых данных должен содержать смежные столбцы. В случае необходимости в поле Константа - ноль можно установить флажок, чтобы линия регрессии прошла через начало координат. В поле Метки установить флажок, если первая строка или первый столбец входного интервала содержит заголовки. В данном случае флажок снят; названия для данных выходного диапазона будут созданы автоматически. В поле Уровень надежности установить флажок, чтобы включить в выходной диапазон дополнительный уровень. В соответствующее поле введите уровень надежности, который будет использован дополнительно к уровню 95 %, применяемому по умолчанию. В нашем случае флажок снят. В поле Выходной диапазон введите ссылку на левую верхнюю ячейку выходного диапазона (ячейка В29). В поле Остатки следует установить флажок для включения остатков в выходной диапазон. В поле Стандартизированные остатки установить флажок для включения стандартизированных остатков в выходной диапазон. Для наглядности изображения можно: • в поле График остатков установить флажок, чтобы построить диаграмму остатков для каждой независимой переменной; • в поле График подбора установить флажок, чтобы построить диаграммы наблюдаемых и предсказанных значений для каждой независимой переменной; • в поле График нормальной вероятности установить флажок, чтобы построить диаграмму нормальной вероятности, и нажать ОК. При выполнении регрессионного анализа на экране появляется отчет, в котором содержится вывод итогов (рисунок 55). 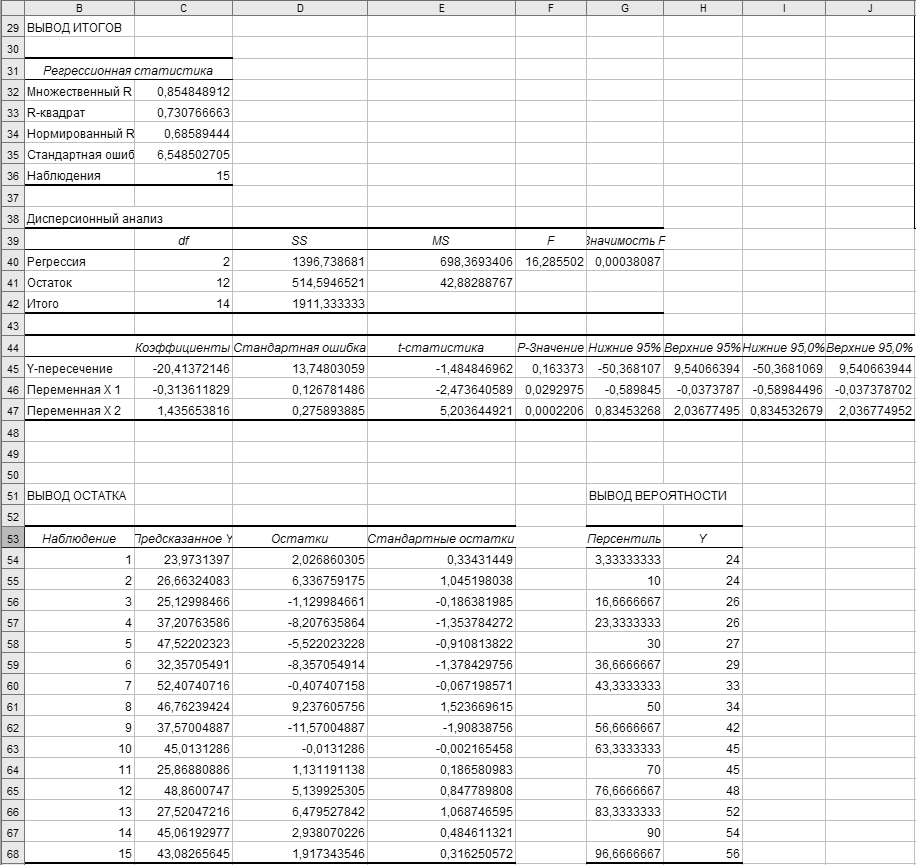 Рисунок 55 – Результат регрессионного анализа Здесь выводятся следующие таблицы итогов: «Регрессионная статистика», «Дисперсионный анализ», «Стандартизированные остатки», «График остатков», «График подбора». В таблице «Регрессионная статистика» выводятся следующие параметры: Коэффициент детерминации, который вычисляется как отношение обусловленной регрессией суммы квадратов SSD к полной сумме квадратов SST. Чем больше R2, тем лучше модель аппроксимирует У. Сравниваются фактические значения у и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминации, нормированный от 0 до 1. Если он равен единице, то имеет место полная корреляция с моделью, т. е. нет различия между фактическим и оценочным значениями у. В противном случае, если коэффициент детерминации равен 0, уравнение регрессии неудачно для предсказания значений у. Множественный коэффициент корреляции оценивает меру линейной зависимости У от всех независимых переменных (в нашем случае от Х1 и X2). Чем ближе к единице, тем сильнее зависимость. Стандартная ошибка или оцениваемое стандартное отклонение для оценки у. Стандартная ошибка оценки параметра регрессии используется для оценки качества подбора функций регрессии. Для этого вычисляется относительный показатель рассеяния, обычно выражаемый в процентах, как корень квадратный из S2. Чем меньше стандартная ошибка, тем более точными будут предсказания. В таблице «Дисперсионный анализ» для модели множественной линейной регрессии приводятся: • df – степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой. • SS – сумма квадратов: обусловленная регрессией сумма квадратов SSD, остаточная сумма квадратов SSr и полная сумма квадратов SST. • MS – средний квадрат: средний квадрат регрессии MSD и средний квадрат отклонения (остатка) от регрессии МSR (величина S2 идентична MSR). • F - F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет. F-отношение определяется как отношение MSD/MSR. В графе «Коэффициенты» приведены значения β0, β1и β2. Постоянная регрессия β0 выполняет в уравнении регрессии функцию выравнивания. Она определяет точку пересечения гиперповерхности регрессии с осью ординат. Значения β1, ..., βm представляют собой оценки коэффициентов регрессии. Полученное уравнение регрессии: ŷ = -20,413721 - 0,3136118Х1 + 1,43565382Х2. Стандартная ошибка определяется как корень квадратный из S̀ β 2. Значимость коэффициента регрессии β1 проверяется с помощью t-критерия и указаны в столбце t-статистики. В столбце Р-значения: если Р<α, то гипотеза H0 отвергается с уровнем значимости α, в противном случае она принимается. В таблице «Вывод остатка» приводятся предсказанные Y. В графе «Остатки» рассчитаны остатки по формуле: наблюдаемая величина Y - предсказанное значение Y. Для получения безразмерной характеристики связи и исключения влияния рассеяния случайных переменных в графе «Стандартные остатки» нормированы отклонения: (наблюдаемая величина Y – предсказанное значение Y)/Sy. 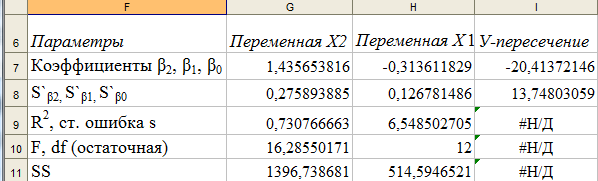 Рисунок 56 – Параметры регрессионного уравнения Для проверки регрессионного анализа воспользуемся функцией ЛИНЕЙН. Сначала подготовим заголовки столбцов таблицы (ячейки F6:I6) и заголовки строк (ячейки F7:F11). В ячейку G7 введем функцию =ИНДЕКС(ЛИНЕЙН ($B$7:$B$21; $C$7:$D$21; 1; 1); 1; 1), где первая единица – номер строки, вторая единица – номер столбца, т. к. массив G7:I11 обрабатывается как матрица. Затем скопируем формулу из ячейки G7 в ячейки G8:G11 и H7:I11 и в формулах заменим номера строк и столбцов соответственно их нумерации в массиве. При расчетах получаются следующие значения (рисунок 56). Уравнение множественной регрессии теперь может быть получено из верхней строки таблицы: ŷ=-20,413721-0,3136118Х1+l,43565382Х2. На основании полученного уравнения необходимо проверить Y, он должен совпасть с Y предсказанным. Для этого нужно создать дополнительный столбец У проверочный в таблице исходных данных, в первой ячейке столбца записать уравнение регрессии через адреса ячеек и скопировать ее на все оставшиеся ячейки столбца. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
