Лабораторная работа. Лабораторная работа1-в.14. Лабораторная работа 1 Определение тепловых эффектов 1 Общие принципы калориметрических измерений

• Название: Лабораторная работа 1 Определение тепловых эффектов 1 Общие принципы калориметрических измерений
• Анкор: Лабораторная работа
• Дата: 02.02.2022
• Размер: 183.78 Kb.
• Имя файла: Лабораторная работа1-в.14.docx
• Тип: Лабораторная работа; #349913

Лабораторная работа № 1

Определение тепловых эффектов
2.1 Общие принципы калориметрических измерений

Все калориметрические измерения имеют много общего. Они заключаются:

а) либо в определении тепловых эффектов процессов. В этом случае надо определить изменение температуры ΔТ в калориметре и, зная теплоёмкость калориметрической системы С_k, вычислить тепловой эффект процесса 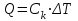(2.1)

б) либо в определении теплоёмкостей, для чего в систему вводят известное количество тепла и наблюдают изменение температуры, тогда: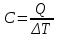

(2.2)

Простейший калориметр с изотермической оболочкой изображен на рисунке 4.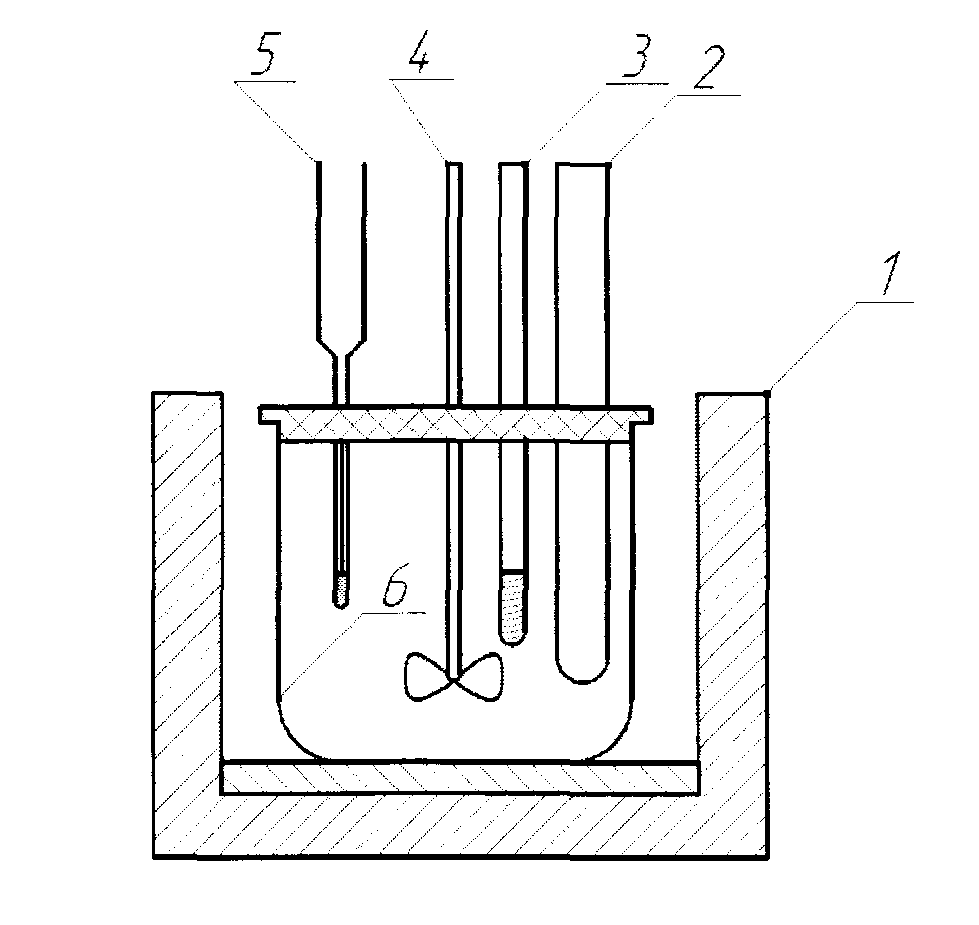


1 - изотермическая оболочка; 2 - пробирка с растворяемым веществом; 3 - нагреватель для введения известного количества тепла; 4 - мешалка; 5- термометр Бекмана; 6 - стакан

Рисунок 4 - Схема калориметра с изотермической оболочкой
2.2 Определение теплоемкости калориметрической системы

Теплоемкость калориметрической системы – количество тепла, необходимое для ее нагревания на 1 градус, то есть .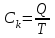

Для этого необходимо ввести в систему (или отнять от системы) известное количество тепла и замерить изменение температуры, вызванное этим процессом.

В калориметрический сосуд наливают 150 - 200 мл дистиллированной воды, зная ее массу (произведение объема на плотность при данной температуре).

В сухую пробирку насыпают 5 г соли КNO₃, хорошо измельченной, взвешенной с точностью до 0,01 г. Теплота растворения КNO₃ в воде равна 34,34 кДж/моль.

Пробирку со взвешенной солью помещают в калориметр через отверстие в крышке калориметра. Туда же вставляют уже настроенный термометр Бекмана. Так как растворение соли КNO₃ идет с поглощением тепла, то столбик ртути в термометре должен быть настроен так, чтобы он находился в верхней части шкалы термометра. Начинают перемешивать жидкость в калориметре, выбрав определенную постоянную частоту перемешивания, и наблюдают за изменением температуры через каждые 30 секунд, которая изменяется вследствие теплообмена всех частей калориметра со средой.

Опыт делится на три периода:

1) Предварительный период - это время, в течение которого устанавливается равномерный ход температуры (примерно по 0,01 - 0,02 градуса за каждые 30 секунд). После установления такого хода температуры делают 8 - 10 замеров, затем быстро высыпают соль из пробирки в воду, вставляют пробирку в то же отверстие (или закрывают отверстие пробкой). Не переставая перемешивать, продолжают наблюдать и записывать температуру. Это начало главного периода.

2) Главный период - это время протекания изучаемого процесса (работа нагревателя или растворения соли). Главный период должен протекать по возможности быстро, чему способствует хорошее перемешивание при растворении соли.

3) Заключительный период. Конец главного периода обнаруживают по вновь установившемуся равномерному ходу температуры. Это заключительный период, в котором делают 8 - 10 замеров.

На основании данных по всем периодам строят график Т =f(t) и графически определяют значение ΔТ (рисунок 5).

Рассмотрим пример (рисунок 5): пусть температура оболочки и стакана равна 25 ⁰С, окружающего воздуха 15 ⁰С, эффект процесса экзотермический. В предварительном периоде (АВ) будет происходить охлаждение калориметрической системы за счет теплообмена с окружающей средой. В главном (ВC) подъем температуры, в заключительном (CД) опять охлаждение за счет теплообмена с окружающей средой, причём с большей скоростью, так как разность температур стала большей. Считаем, что в первой половине главного периода теплообмен идет как в предварительном периоде, а во второй половине как в заключительном. Делим весь главный период на равные части (точка Е). Экстраполируем ход температуры в предварительном периоде до точки М, в заключительном до точки N. Полученные точки М и N экстраполируем на ось температуры и определяем ΔТ = Т₂-T₁.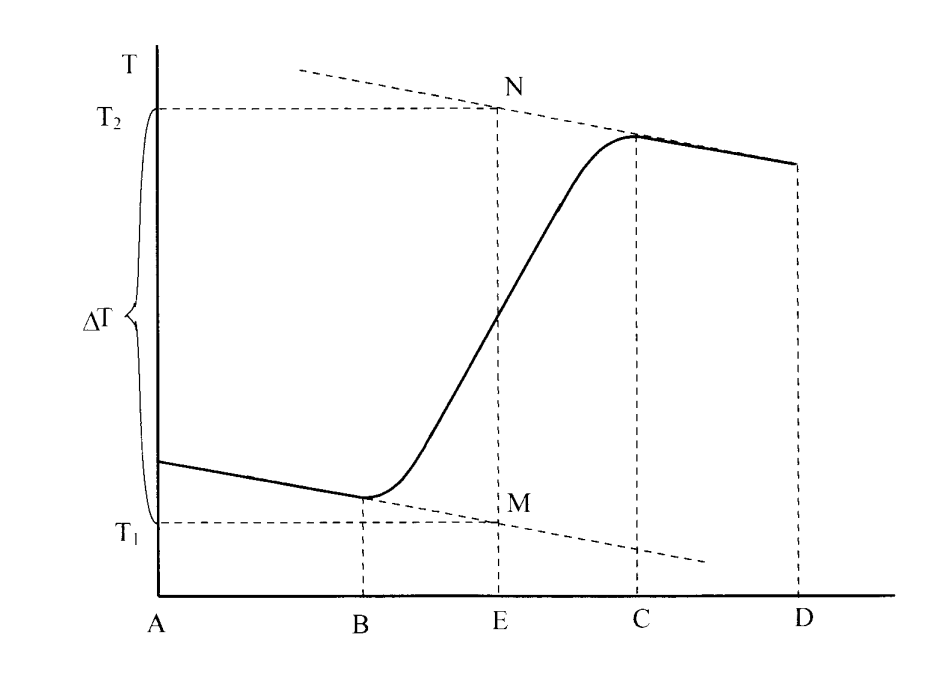



Рисунок 5 - Графический способ определения ΔТ

2.3 Расчет постоянной калориметра

1) При определении тепловых эффектов постоянной калориметра является теплоемкость всех частей калориметра совместно с растворителем: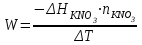

, (2.3)

где 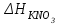= 34,34·10³ Дж/моль - теплота растворения КNO₃, n -количество КNO₃, моль; ΔТ — изменение температуры, в градусах, (Т=Т₂ – Т₁).

2) Определение теплоемкости жидкостей .

В этом случае постоянной сосуда является теплоемкость только частей калориметра без растворителя :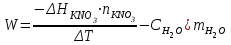

, (2.4)

где 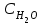- удельная теплоемкость воды, равная при 298 К 4,183 Дж/г·К; 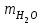масса воды, г.

Работа 1.

Определение теплоты растворения хорошо растворимой соли
Цель работы: определить теплоту растворения соли (КСI, NaCl, NaNO₃, K₂SO₄, NH₄NO₃, CuSO₄, соль выдается преподавателем). Нам был выдан нитрат натрия.

Порядок выполнения работы:

Собирают калориметр (рисунок 4) и определяют его постоянную (W, как описано в пунктах 2.2 и 2.3).

Опыт повторяют с солью, тепловой эффект растворения которой следует определить. Для этого взвешивают 5 - 6 грамм мелко растертой исследуемой соли и проводят ее растворение аналогично соли КNO₃.

Полученные данные используют для нахождения ΔТ графическим методом для исследуемой соли. Теплота процесса растворения рассчитывается по формуле: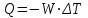

, (2.5)

Далее рассчитываем удельную (Дж/г) и молярную (Дж/моль) теплоты растворения: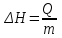

, (2.6)

где m – масса соли,г.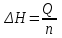

, (2.7)

где n – количество вещества соли, моль.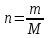

, (2.8)

где М – молярная масса соли, г/моль.
Расчётная часть:

1. 
   Находим постоянную калориметра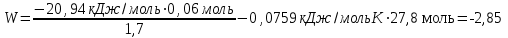
   

2. 
   _{Находим теплоту растворения нитрата натрия}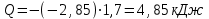
   

3. 
   Находим удельную и молярную теплоты растворения _{нитрата натрия}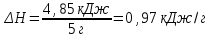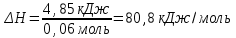
   

Работа 2.

Определение теплоты гидратообразования
Цель работы: определить тепловой эффект образования кристаллогидрата соли СuSО₄ ·5Н₂О.

Порядок выполнения работы:

Собирают калориметр (рисунок 4).

Определяют постоянную калориметра (описано в пунктах 2.2 и 2.3).

Определение теплоты образования кристаллогидрата сводится к измерению теплоты растворения безводной соли и кристаллогидрата так, чтобы концентрации растворов обеих солей были одинаковы (1 моль соли на 200 молей воды). Рассчитайте массу навесок СuSО₄ и СuSО₄ ·5Н₂О для растворения в 150 мл воды.

Навески солей взвешивают с точностью до 0,01 г. Опыт сначала проводят с одной солью СuSО₄, находят ΔТ₁, затем с другой солью СuSО₄ ·5Н₂О, находят ΔТ₂. Опыт ведут как описано пунктах 2.2 и 2.3. ΔТ₁ и ΔТ₂ определяют графически.

Рассчитывают тепловые эффекты растворения солей (по формулам 2.5, 2.6, 2.7), рассчитывают молярную теплоту гидратообразования по уравнению: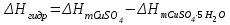

(2.9)
Расчётная часть:

1. 
   Находим постоянную калориметра для медного купороса и сульфата меди (II) безводного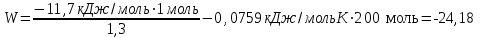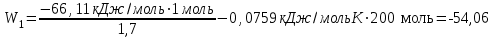
   

2. 
   Находим теплоту растворения медного купороса и сульфата меди (II) безводного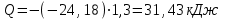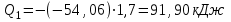
   

3. 
   Находим удельную теплоту растворения медного купороса и сульфата меди (II) безводного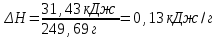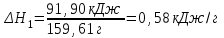
   

4. 
   _{Находим молярную теплот}у растворения медного купороса и сульфата меди (II) безводного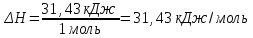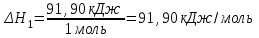
   

5. 
   Находим теплоту гидратообразования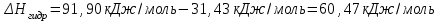
   

Работа 3.

Определение теплоты диссоциации слабого электролита
Цель работы: определить теплоту диссоциации слабого основания (NH₄OH).

Тепловой эффект нейтрализации сильной кислоты сильным основанием равен тепловому эффекту образования молекул из ионов Н⁺+ОН^- (ΔН_нейтр). Теплота нейтрализации слабого основания (NH₄OH) сильной кислотой, 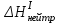, равна сумме:

1. 
   теплоты диссоциации слабого основания (ΔН_дисс);
   

б) теплоты образования воды из ионов Н⁺+ОН^- (ΔН_нейтр).

Порядок выполнения работы:

Собирают калориметр (рисунок 4);

Определяют постоянную калориметра (пункты 2.2 и 2.3);

Определяют теплоту нейтрализации сначала сильного, затем слабого основания сильной кислотой. Для этого в калориметр наливают 150 мл 0,1 н сильного основания; в пробирку вливают 5 мл 4 н серной кислоты. Пробирку вставляют в калориметр через отверстие в крышке. Сначала проводят предварительный период, пока температура не станет изменяться на 0,01 – 0,02 градуса. Затем содержимое пробирки выливают через отверстие в крышке калориметра через воронку. Продолжают следить за изменением температуры, проводя главный и заключительные периоды. Графически определяют ΔТ.

Рассчитывают молярную теплоту нейтрализации сильного основания: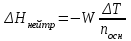

, (2.10)

где n_осн – количество нейтрализованного основания, моль.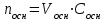

, (2.11)

где С_осн – концентрация взятого основания, моль/л.

Затем подобным образом нейтрализуют слабое основание и рассчитывают .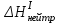

Полученные теплоты нейтрализации используют для расчета теплоты диссоциации: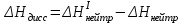

, (2.12)
Расчётная часть:

1. 
   Находим постоянную калориметра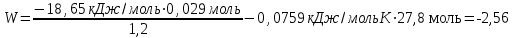
   

2. 
   Находим молярную теплоту нейтрализации сильного основания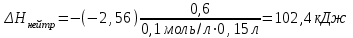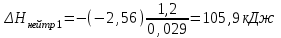
   

3. 
   Находим молярную теплоту нейтрализации слабого основания
   

4. 
   Находим теплоту диссоциации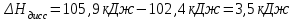
   

Работа 4.

Измерение теплоемкости веществ
Цель работы: определить теплоемкость раствора MgSO₄.
4.1 Порядок проведения эксперимента

Для определения теплоемкости какой-либо жидкости проводят два опыта. В одном – отнимают или вносят определенное количество тепла от жидкости с известной теплоемкостью (чаще всего воды):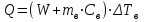

, (2.13)

где m_в, С_в, ΔТ_в – соответственно масса, теплоемкость и изменение температуры в опыте с водой.

Во втором – это же тепло отнимают от жидкости с неизвестной теплоемкостью: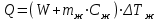

, (2.14)

Измерение ΔТ для определения теплоемкости веществ проводится методом введения охлажденного тепла (калорифера) в калориметр. В качестве калорифера используют пробирку с бензолом. В пробирку налито 5 мл бензола. Пробирка закрывается пробкой со вставленным в нее термометром. Калорифер помещают в стакан со смесью мелко раздробленного льда и небольшого количества воды.

4.2 Определение ∆Т воды

Наливают в калориметрический сосуд 150- 200 мл дистиллированной воды, закрывают крышкой и в соответствующее отверстие вставляют термометр Бекмана, настроенный таким образом, чтобы мениск ртути находился выше средней части шкалы. Второе отверстие для пробирки закрывают пробкой и ведут предварительный период, постоянно помешивая воду и замечая изменение температуры через каждые 30 секунд. После установления равномерного хода изменения температуры на 0,01 - 0,02 градуса вынимают калорифер из охлаждающей смеси и быстро вставляют в отверстие в крышке калориметрического сосуда, замечают изменение температуры через 30 секунд, не прекращая перемешивания воды. При этом происходит нагревание и плавление бензола (главный период), температура понижается за счет отнятия тепла у воды на плавление бензола. Когда весь бензол расплавится, начинается повышение температуры (заключительный период). Записывают 10 показаний термометра заключительного периода и опыт прекращают. ∆Т определяют графически.
4.3 Определение ∆Т жидкости

В калориметрический сосуд наливают 150 - 200 мл исследуемой жидкости (раствор MgSO₄), замораживают бензол и опыт ведут как описано выше. Температура замерзания бензола должна быть точно такой же, как и при определении ∆Т воды. Определяют ∆Т жидкости графически и рассчитывают теплоемкость жидкости С_ж, приравнивая уравнения: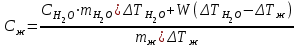

, (2.15)

где .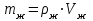

Расчётная часть:

1. 
   Находим количество тепла воды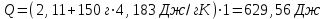
   

2. 
   Находим теплоёмкость сульфата магния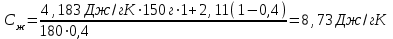
   

Выводы: Таким образом, нами была определена теплота растворения хлорида калия, определён тепловой эффект образования кристаллогидрата соли СuSО₄·5Н₂О, определена теплота диссоциации слабого основания на примере NH₄OH, определена теплоемкость раствора MgSO₄

Вариант 14
Задание 1

Зависимость теплового эффекта от температуры: анализ уравнения Кирхгофа.

Решение:

В общем случае тепловой эффект химической реакции зависит от температуры и давления, при которых проводится реакция. Влиянием давления на ΔН и ΔU реакции обычно пренебрегают. Влияние температуры на величины тепловых эффектов описывает закон Кирхгофа:

Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции.

Продифференцируем ΔН и ΔU по температуре при постоянных давлении и температуре соответственно:

 (I.22)

 (I.23)

Производные энтальпии и внутренней энергии системы по температуре есть теплоемкости системы в изобарных и изохорных условиях C_p и C_v соответственно:

 (I.24)

 (I.25)

Подставив выражения (I.24, I.25) в (I.22, I.23), получаем математическую запись закона Кирхгофа:

 (I.26)

 (I.27)

Для химического процесса изменение теплоемкости задается изменением состава системы и рассчитывается следующим образом:

 (I.28)

 (I.29)

Если проинтегрировать выражения (I.26, I.27) от Т = Т₁ до Т = Т₂, считая ΔС_p (ΔС_v) не зависящим от температуры, получим интегральную форму закона Кирхгофа:

 (I.30)

 (I.31)

Поскольку обычно известны табличные значения стандартных тепловых эффектов ΔН°₂₉₈ и ΔU°₂₉₈, преобразуем выражения (I.30, I.31):

 (I.32)

 (I.33)

При расчете изменения теплового эффекта реакции в большом интервале температур необходимо учитывать зависимость теплоёмкости от температуры, которая выражается степенным рядом C°_p = aT + bT² + cT³; коэффициенты a, b, c приведены в справочниках.
Задание 2

5 моль одноатомного и 5 моль двухатомного газа изохорически нагревается на 20 ⁰С. Для какого газа требуется больше теплоты?

Решение: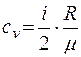





i – число степеней свободы. Для одноатомного газа i = 3, для двухатомного газа i = 5.

Таким образом, для изохорического нагрева 5 моль двухатомного газа нужно больше теплоты, чем для изохорического нагрева 5 моль одноатомного газа.