Лабораторная работа 1 По дисциплине_ Теория телетрафика и анализ. Лабораторная работа 1 По дисциплине Теория телетрафика и анализ систем беспроводной связи
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Федеральное агентство связи Федеральное государственное бюджетное образовательное учреждение высшего образования Сибирский государственный университет телекоммуникаций и информатики ЛАБОРАТОРНАЯ РАБОТА 1По дисциплине: Теория телетрафика и анализ систем беспроводной связиПрименение B-формулы Эрланга в сетях с коммутацией каналов Выполнил: Группа: Проверил: Новосибирск, 2022 г Содержание ЛАБОРАТОРНАЯ РАБОТА 1 1 По дисциплине: Теория телетрафика и анализ систем беспроводной связи 1 Описание 5 Диаграмма интенсивностей переходов 6 Вероятности и 6 ЛАБОРАТОРНАЯ РАБОТА 2 9 ЛАБОРАТОРНАЯ РАБОТА 3 26 Цель работы: Освоить применение формулы Эрланга для расчёта вероятности блокировки системы и необходимого количества каналов в сети. Задание: В лабораторной работе, задавая сетевые параметры в соответствии с вариантом, необходимо произвести расчёт вероятности блокировки 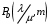 по ф. (7.21) и построить её зависимости от входной нагрузки по ф. (7.21) и построить её зависимости от входной нагрузки 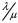 и количества каналов m. Затем, используя рекуррентное соотношение ф. (7.22) определить число каналов, необходимое для обеспечения заданного значения вероятности блокировки в соответствии с вариантом. Построить зависимость количества каналов от входной нагрузки и количества каналов m. Затем, используя рекуррентное соотношение ф. (7.22) определить число каналов, необходимое для обеспечения заданного значения вероятности блокировки в соответствии с вариантом. Построить зависимость количества каналов от входной нагрузки 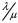 . .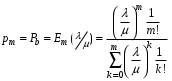 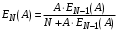 где: 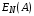 – вероятность блокировки при заданных значениях нагрузки A и числа каналов N; – вероятность блокировки при заданных значениях нагрузки A и числа каналов N; 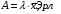 – нагрузка, измеряемая в Эрлангах. Начальным значением для рекуррентного вычисления вероятности блокировки является: – нагрузка, измеряемая в Эрлангах. Начальным значением для рекуррентного вычисления вероятности блокировки является: 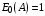 . .Для соблюдения равенства Pb = 0.03 найдем параметры зависимости m и Y
   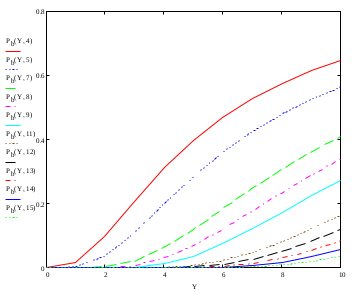 Рисунок 1 - Зависимость вероятности блокировки от входной нагрузки при различных значениях количества каналов в сети Вывод: Из анализа графика следует, что вероятность блокировки от увеличения входной нагрузки возрастает значительнее при меньшем количестве каналов в сети. Количество каналов влияет на изменение вероятности блокировки при различных входных нагрузках. 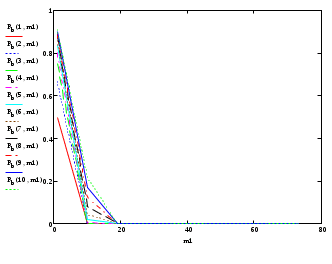 Рисунок 2 -Зависимость вероятности блокировки от количества каналов при различных значениях нагрузки в сети Вывод: Из анализа графика следует, что при меньшем количестве каналов в сети при малой нагрузки вероятность блокировки снижается.   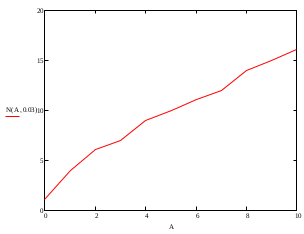 Рисунок 3 -Зависимость количества каналов от входной нагрузки Вывод: Из анализа графика следует, что при заданной вероятности блокировки 0,03 зависимость количества каналов от входной нагрузки возрастает линейно, чем больше нагрузка, тем больше каналов необходимо. Вывод по работе: В ходе выполнения лабораторной работы мы научились осваивать применение формулы Эрланга для расчёта вероятности блокировки системы и необходимого количества каналов в сети. Определили, что количество каналов при нагрузке влияет на изменения блокировки ошибок. Контрольные вопросы: Дайте определение системы массового обслуживания. Сеть массового обслуживания (СеМО) – это совокупность систем массового обслуживания (СМО) с различными интенсивностями обслуживания, в которой циркулирует некоторое количество заявок различных классов, обсуживаемых в соответствии с заданной дисциплиной Дайте определения процесса размножения и гибели. Рассмотрим еще одну типичную схему непрерывных марковских цепей - так называемую схему гибели и размножения, часто встречающуюся в разнообразных практических задачах. Марковский процесс с дискретными состояниями S0, S1, ..., Sn называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S1, S2, ...,Sn-1) может переходить только в соседние состояния, которые, в свою очередь, переходят обратно, а крайние состояния (S0 и Sn) переходят только в соседние состояния (рис. 3.7). Название взято из биологических задач, где состояние популяции Sk означает наличие в ней k единиц особей. Переход вправо связан с размножением единиц, а влево - с их гибелью. 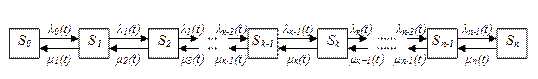 Граф состояний для процесса гибели и размножения l0(t), l1(t), l2(t), …, ln(t) - интенсивности размножения; m1(t), m2(t), …, mn(t) - интенсивности гибели. У l и μ индекс того состояния, из которою стрелка выходит. С состоянием Sk связана неслучайная величина Хk: если система S в момент времени t находится в состоянии Sk, то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс Х(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние. Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным. В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой «гибели» называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю. Приведите особенности модели Эрланга. |
