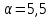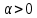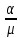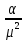Лабораторная работа 1 По дисциплине_ Теория телетрафика и анализ. Лабораторная работа 1 По дисциплине Теория телетрафика и анализ систем беспроводной связи
 Скачать 0.61 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА 2По дисциплине: Теория телетрафика и анализ систем беспроводной связи Применение формулы Полячека-Хинчина Выполнил: Группа: Проверила: Новосибирск 2022, г Содержание ЛАБОРАТОРНАЯ РАБОТА 1 1 По дисциплине: Теория телетрафика и анализ систем беспроводной связи 1 Описание 5 Диаграмма интенсивностей переходов 6 Вероятности и 6 ЛАБОРАТОРНАЯ РАБОТА 2 9 ЛАБОРАТОРНАЯ РАБОТА 3 26 Цель работы: Изучить применение формулы Полячека-Хинчина для вычисления вероятностно-временных характеристик систем массового обслуживания с произвольным распределением времени обслуживания. Задание: В данной лабораторной работе предполагается сравнить вероятностно-временные характеристики систем массового обслуживания типа M/M/1, M/D/1, полученные с помощью формул Полячека-Хинчина с характеристиками СМО, заданного по варианту типа (табл. 2). Используя данные из табл. 2, задать параметры исследуемых систем массового обслуживания. Вычислить значения нормированной дисперсии исследуемых СМО ф. (8.6). Для вычисления математического ожидания и дисперсии воспользоваться любым справочником по теории вероятностей и математической статистике, например, [5] (или см. ПРИЛОЖЕНИЕ 1). По ф. (8.7)–(8.10) получить искомые характеристики: - среднее количество заявок в СМО ; - среднее количество заявок в очереди СМО ; - среднее время пребывания заявки в СМО ; - среднее время ожидания заявкой обслуживания . Примечание 5: При этом диапазон изменения интенсивности входящего в СМО потока заявок задать, начиная с 0, и таким образом, чтобы сохранить эргодичность системы . Построить семейство зависимостей описанных выше характеристик от входной нагрузки для различных СМО. Объяснить полученные результаты. Таблица 2 – Параметры для выполнения лабораторной работы № 2 вариант 8
2 Выполнение лабораторной работы в соответствии с заданием с описанием всех значащих этапов Определим параметры моделируемых СМО в соответствии с вариантом (табл. 2): - интенсивность обслуживания прибора 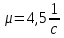 ;- параметр масштаба 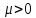 - параметр формы: порядок 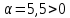 - мат. ожидание 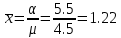 - нормированную дисперсию времени обслуживания для каждой СМО: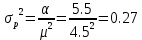 
Разработаем функцию(и) для расчёта вероятностно-временных характеристик СМО по формуле Полячека-Хинчина в соответствии с заданием. Среднее количество заявок в СМО типа M/G/1: , (2.1) где ρ – коэффициент загрузки СМО, ; – второй момент распределения времени обслуживания . Введём нормированную дисперсию времени обслуживания (дисперсия времени обслуживания, нормированная по квадрату математического ожидания времени обслуживания): . (2.2) Тогда выражение (2.1) будет выглядеть следующим образом: . (2.3) Ф. (2.1) и (2.3) называют формулой Полячека-Хинчина для среднего числа заявок в СМО. Можно выразить среднее число заявок в очереди: , (2.4) а также среднее время пребывания заявки в системе, используя формулу Литтла: . ; (2.5) и среднее время пребывания в очереди: , (2.6) из . Рассмотрим систему M/M/1. Зная, что для данной СМО среднее время обслуживания: , а дисперсия , определим нормированную дисперсию: . Подставляем в выражение (2.3): . Разработаем функцию(и) для расчёта вероятностно-временных характеристик СМО по формуле Полячека-Хинчина в соответствии с заданием. 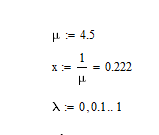 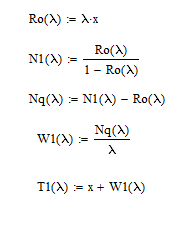 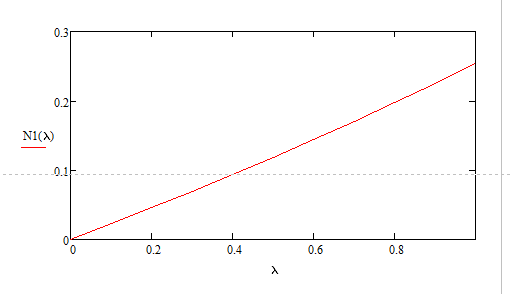 Рисунок 1 - Зависимость среднего количества заявок от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок резко возрастает. 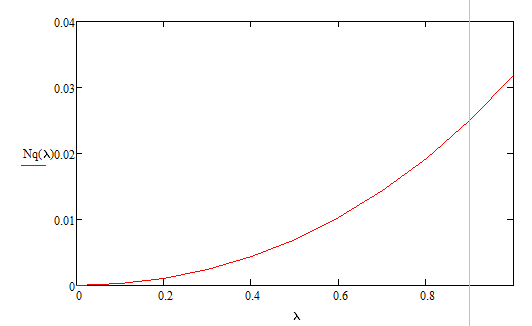 Рисунок 2 - Зависимость среднего числа заявок в очереди от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок в очереди резко возрастает. 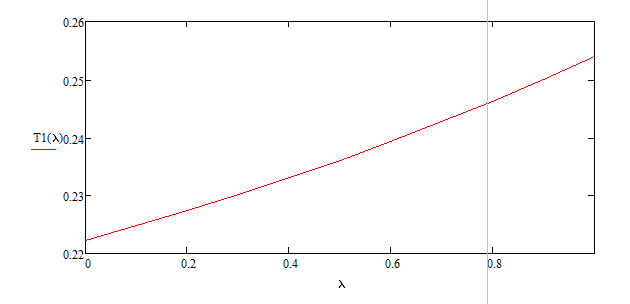 Рисунок 3 - Зависимость среднего времени пребывания заявки в системе от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в системе возрастает. 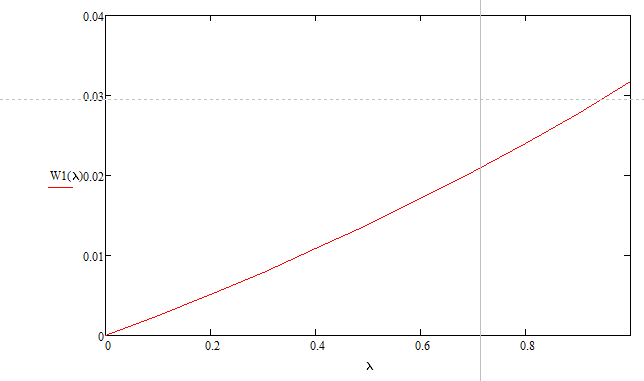 Рисунок 4 - Зависимость среднего времени пребывания заявки в очереди от входной нагрузкиВывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в очереди возрастает. Рассмотрим систему M/D/1. В СМО с постоянным временем обслуживания его дисперсия . Следовательно, нормированная дисперсия . Что дает: Разработаем функцию(и) для расчёта вероятностно-временных характеристик СМО по формуле Полячека-Хинчина в соответствии с заданием. 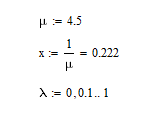 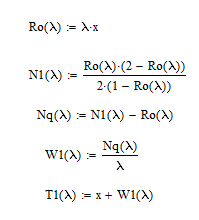 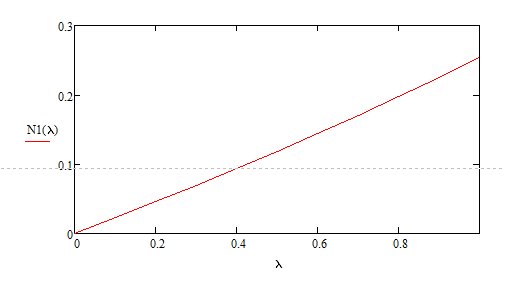 Рисунок 5 - Зависимость среднего количества заявок от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок резко возрастает. 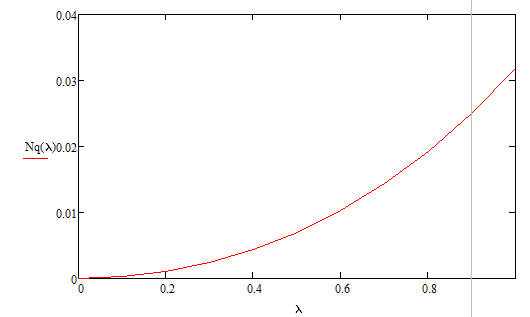 Рисунок 6 - Зависимость среднего числа заявок в очереди от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок в очереди резко возрастает. 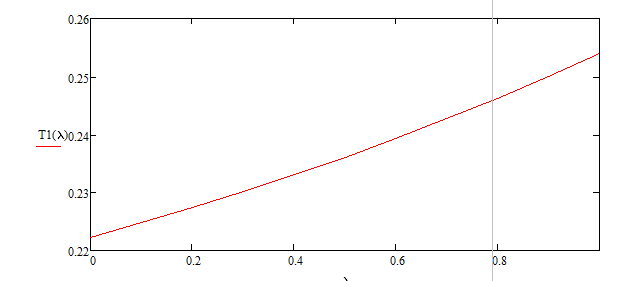 Рисунок 7 - Зависимость среднего времени пребывания заявки в системе от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в системе возрастает. 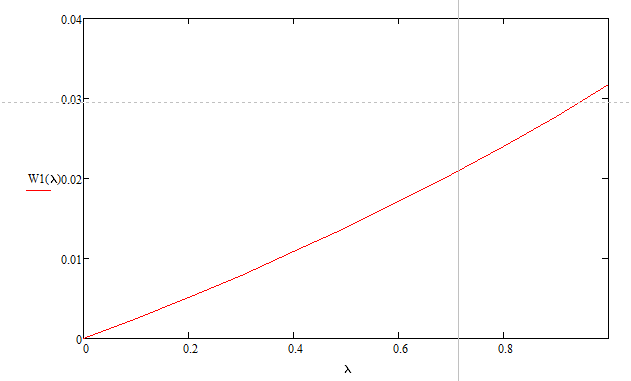 Рисунок 8 - Зависимость среднего времени пребывания заявки в очереди от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в очереди возрастает. При рассмотрении систем типа M/M/1 и M/D/1 установлено, что в системе типа M/M/1 с в отличии от M/D/1 с возрастанием входной нагрузки такие зависимости, как среднее время ожидания заявкой обслуживания, среднее время пребывания заявки, среднее время пребывания заявки в очереди и среднее количества заявок возрастают примерно в 2 раза быстрее. Заданная система. Рассмотрим СМО типа M/G/1, на входе которой простейший поток требований с параметром . Интенсивность обслуживания прибора 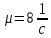 . Время обслуживания распределено по закону гиперэкспоненциальное 2-го порядка.Разработаем функцию(и) для расчёта вероятностно-временных характеристик СМО по формуле Полячека-Хинчина в соответствии с заданием. 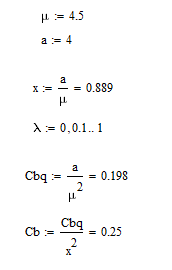 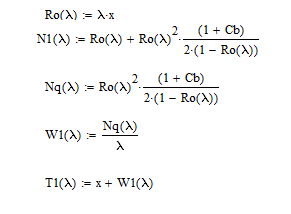 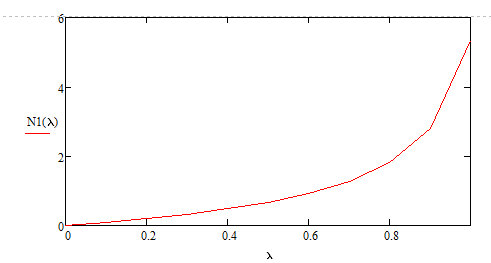 Рисунок 9 - Зависимость среднего количества заявок от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок резко возрастает. 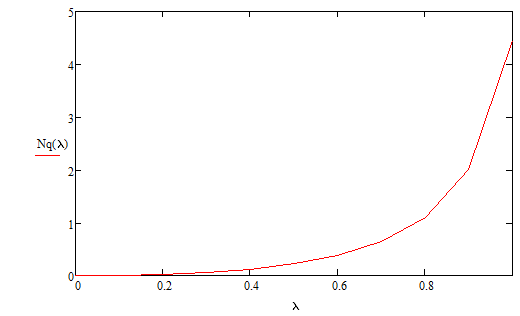 Рисунок 10 - Зависимость среднего числа заявок в очереди от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее число заявок в очереди резко возрастает. 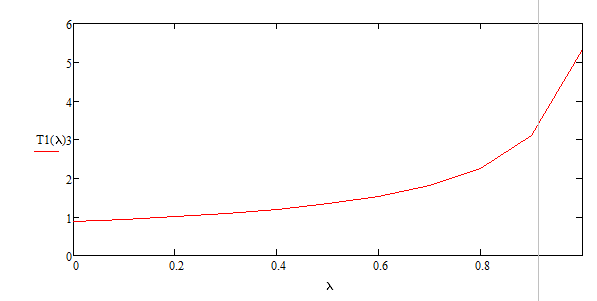 Рисунок 11 - Зависимость среднего времени пребывания заявки в системе от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в системе возрастает. 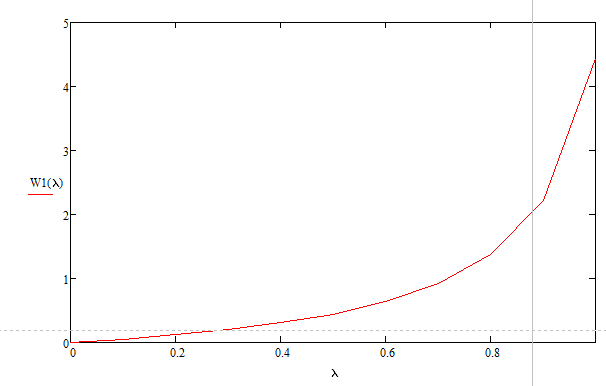 Рисунок 12 - Зависимость среднего времени пребывания заявки в очереди от входной нагрузки Вывод: Проведя анализ графика установлено, что с увеличением входной нагрузки среднее время пребывания заявок в очереди возрастает. Построим 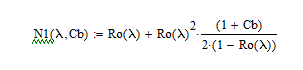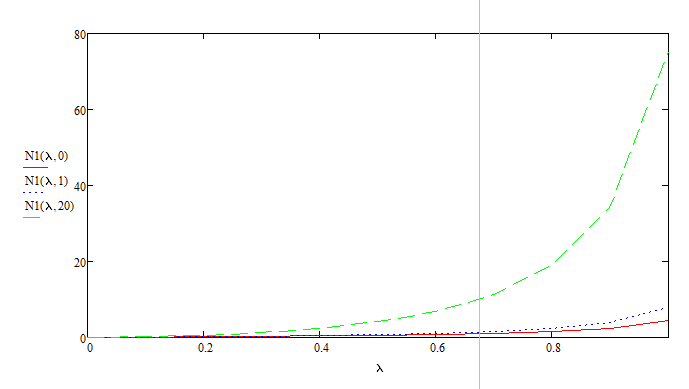зависимости полученных значений от интенсивности входной нагрузки для СМО разного типа, отличающихся значением нормированной дисперсии.   Рисунок 13 - Зависимости полученных значений от интенсивности входной нагрузки для СМО разного типа, отличающихся значением нормированной дисперсииВывод: Анализируя график зависимости полученных значений от интенсивности входной нагрузки для СМО разного типа, отличающихся значением нормированной дисперсии установлено, чем выше нормированная дисперсия, тем выше значения от интенсивности входной нагрузки. 3 Вывод по работе В ходе лабораторной работы мной было изучено применение формулы Полячека-Хинчина для вычисления вероятностно-временных характеристик систем массового обслуживания с распределением гиперэкспоненциальное 2-го порядка времени обслуживания Получены и проанализированы вероятностно-временные характеристики систем массового обслуживания типа M/M/1, M/D/1 с помощью формул Полячека-Хинчина с характеристиками СМО, заданного по варианту типа. Вероятностно-временные характеристики исследуемой системы значительно отличаются от систем типа M/M/1, M/D/1. Зависимость среднего количества заявок от входной нагрузки ниже, чем типа M/M/1, M/D/1 Зависимость среднего время пребывания заявки в очереди от входной нагрузки выше, чем типа M/M/1, M/D/1. Зависимость среднего время пребывания заявки от входной нагрузки выше, чем типа M/M/1, M/D/1 Зависимость среднего времени ожидания заявкой обслуживания от входной нагрузки выше, чем типа M/M/1, M/D/1 4 Контрольные вопросы Опишите систему массового обслуживания M/G/1. Система массового обслуживания M/G/1 – это однолинейная система с пуассоновским входящим потоком и произвольным распределением времени обслуживания , с плотностью . Распределение промежутков времени между поступлениями заявок – показательное [4, 8]: , с плотностью распределения: , – интенсивность входящего потока (заявок в секунду). Средний промежуток времени между поступлениями дисперсия – . Состояние системы M/G/1 описывается вектором, состоящим из: – число требований в системе в момент t. – время обслуживания, которое к данному моменту получило требование, находящиеся в приборе. Его необходимо учитывать, так как процесс обслуживания в общем случае не является процессом без последействия, т.е. – израсходованная часть времени обслуживания. Почему анализ системы с последействием затруднён? Кроме того, анализ СМО усложняется тем обстоятельством, что является дискретной величиной, а – непрерывной. В качестве метода исследования принят метод вложенной цепи Маркова. В чём заключается метод вложенной цепи Маркова? Основная идея данного метода, состоит в том, чтобы упростить описание состояний, заменив двумерное описание одномерным . Для того, чтобы вычислять будущие значения случайных величин, вместе с числом заявок в системе нужно неявно задавать время, проведённое требованием в приборе обслуживания. Можно добиться упрощения, рассматривая не все моменты времени, а определённую их последовательность, выбранную таким образом, чтобы, задавая число требований в системе в один из таких моментов и обеспечив дальнейшее поступление требований в систему, можно было вычислить число заявок в системе в следующий принадлежащий последовательности момент. Особенно удобна последовательность моментов ухода обслуженных требований [4, 8]. Определив число заявок в момент, когда обслуженное требование покидает систему, и прибавив число поступивших позже требований, можно найти число требований в системе для любого момента времени в будущем. В момент времени ухода обслуженного требования время, потраченное на обслуживание следующего требования равно нулю, так как обслуживание в этот момент только начинается. Описанный процесс является полумарковским процессом, при котором изменения состояний происходят в момент ухода очередного обслуженного требования. Для таких моментов определим вложенную цепь Маркова как число заявок, имеющихся в системе в момент ухода очередного обслуженного требования. Переходы из состояния в состояние имеют место только во вложенных точках и образуют дискретное пространство состояний. Как выглядит матрица вероятностей переходов вложенной цепи Маркова? Нас интересует распределение вероятностей , то есть , которое зависит от времени. Предельное распределение при совпадает с : . Определим вероятность перехода за один шаг (для Марковской цепи): . (8.1) Поскольку переходы соответствуют уходам заявок из СМО, то не выполняется условие: , и, напротив, условие возможно для любого . Тогда матрица переходов : ; (8.2) где . Например, j-й элемент первой спирали матрицы представляет собой вероятность того, что предыдущее требование, уходя, оставило систему пустой, а за время обслуживания заявки поступает j новых требований. Любой элемент при представляет собой вероятность поступления точно заявок за время обслуживания при условии, что , уходя, оставило точно i требований, одно из которых сразу поступает на обслуживание. На рисунке 8.3 показаны только переходы из состояния . Дайте пояснения к правой части формулы Полячека-Хинчина. Формула служит для предварительной оценки среднего количества заявок, а также зависящих от него характеристик в системе с пуассоновским входящим потоком. Что такое нормированная дисперсия времени обслуживания? дисперсия времени обслуживания, нормированная по квадрату математического ожидания времени обслуживания Список литературы Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с. Башарин, Г.П. Лекции по математической теории телетрафика [Электронный ресурс]: учебное пособие. – М.: Российский университет дружбы народов, 2009. – 146 c. – Режим доступа: http://www.iprbookshop.ru/11564.html по паролю. Вентцель Е.С. Теория вероятностей: учебник. – М.: КНОРУС, 2010. – 664 с. Иверсен В.Б. Разработка телетрафика и планирование сетей. Учеб. пособие. – М.: Нац. Открытый Ун-т «ИНТУИТ»: Бином. Лаборатория знаний, 2011. – 526 с. Вадзинский P.H. Справочник по вероятностным распределениям. – CП6.: Наука, 2001. – 295 с. Вишневский В.М. Теоретические основы проектирования компьютерных сетей // Москва: Техносфера, 2003. – 512 с. Кокорева, Е. В. Анализ сетей массового обслуживания [Электронный ресурс]: учебно-методическое пособие / Новосибирск: Сибирский государственный университет телекоммуникаций и информатики, 2015. – 39 c. – Режим доступа: http://www.iprbookshop.ru/55468.html по паролю. Башарин Г.П., Толмачев А.Л. Теория сетей массового обслуживания и ее приложения к анализу информационно-вычислительных систем [Электронный ресурс] // Итоги науки и техники: Сер. Теор. вероятн. Мат. стат. Теор. кибернет., 21, ВИНИТИ. – М., 1983, С. 3-19. – Режим доступа: http://www.mathnet.ru/links/4d33dbf1daca533be0933bb49245aa72/intv56.pdf Федеральное агентство связи Федеральное государственное бюджетное образовательное учреждение высшего образования Сибирский государственный университет телекоммуникаций и информатики | ||||||||||||||||||||||
