Лабораторная работа 1 По дисциплине_ Теория телетрафика и анализ. Лабораторная работа 1 По дисциплине Теория телетрафика и анализ систем беспроводной связи

• Название: Лабораторная работа 1 По дисциплине Теория телетрафика и анализ систем беспроводной связи
• Дата: 12.08.2022
• Размер: 0.61 Mb.
• Имя файла: Лабораторная работа 1 По дисциплине_ Теория телетрафика и анализ.docx
• Тип: Лабораторная работа; #644842
• страница: 4 из 5

ЛАБОРАТОРНАЯ РАБОТА 3

По дисциплине: Теория телетрафика и анализ систем беспроводной связи

Уравнения глобального баланса

Выполнил:

Группа:

Проверила:

Новосибирск, 2022 г.
Содержание

ЛАБОРАТОРНАЯ РАБОТА 1 1

По дисциплине: Теория телетрафика и анализ систем беспроводной связи 1

Описание 5

Диаграмма интенсивностей переходов 6

Вероятности и 6

ЛАБОРАТОРНАЯ РАБОТА 2 9

ЛАБОРАТОРНАЯ РАБОТА 3 26

Цель работы: Научиться составлять и решать системы уравнений глобального баланса для анализа замкнутых однородных марковских СеМО, а также применять результаты расчёта для вычисления узловых и сетевых характеристик СеМО.

Схема

Считать все СМО – марковскими с дисциплинами обслуживания – FCFS.

Количество заявок в СеМО, состоящих из трёх узлов (1–4, 7, 10) , в СеМО, состоящих из четырёх узлов (5, 6, 8, 9, 11–15) – .

µ, c-1	m	ТОПОЛОГИЯ
		1
2,1 2,5 2,8 3,0	2,3,3,1	8

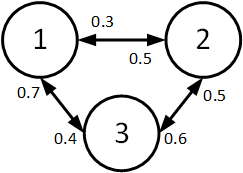
РЕШЕНИЕ

Маршрутная матрица: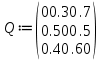


Коэффициенты переходов:

e1= 0.5e2+0.4e3

e2= 0.3e1+0.6e3

e3= 0.7e1+0.5e2

Для решения принимаем e1 = 1.

е2 = 1,029

е3=1,214
Относительный коэффициент загрузки узлов:

b1=e1/μ1=1/2,1=0,476

b2=e2/μ2=1,029/2,5=0,411

b3=e3/μ3=1,214/2,8=0,434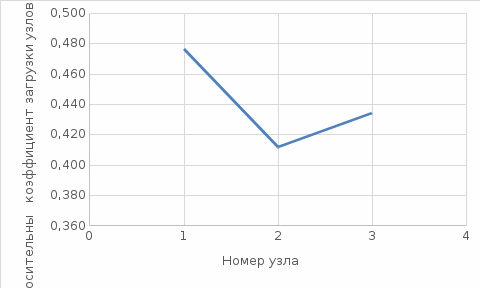


Рисунок 1 – График зависимости относительного коэффициента загрузки узла от номера узла

Пространство состояний:

(3,0,0), (0,3,0), (0,0,3),

S(3,3)= (2,1,0), (0,2,1), (0,1,2),

(1,2,0), (1,0,2), (2,0,1), (1,1,1)

Диаграмма интенсивностей переходов: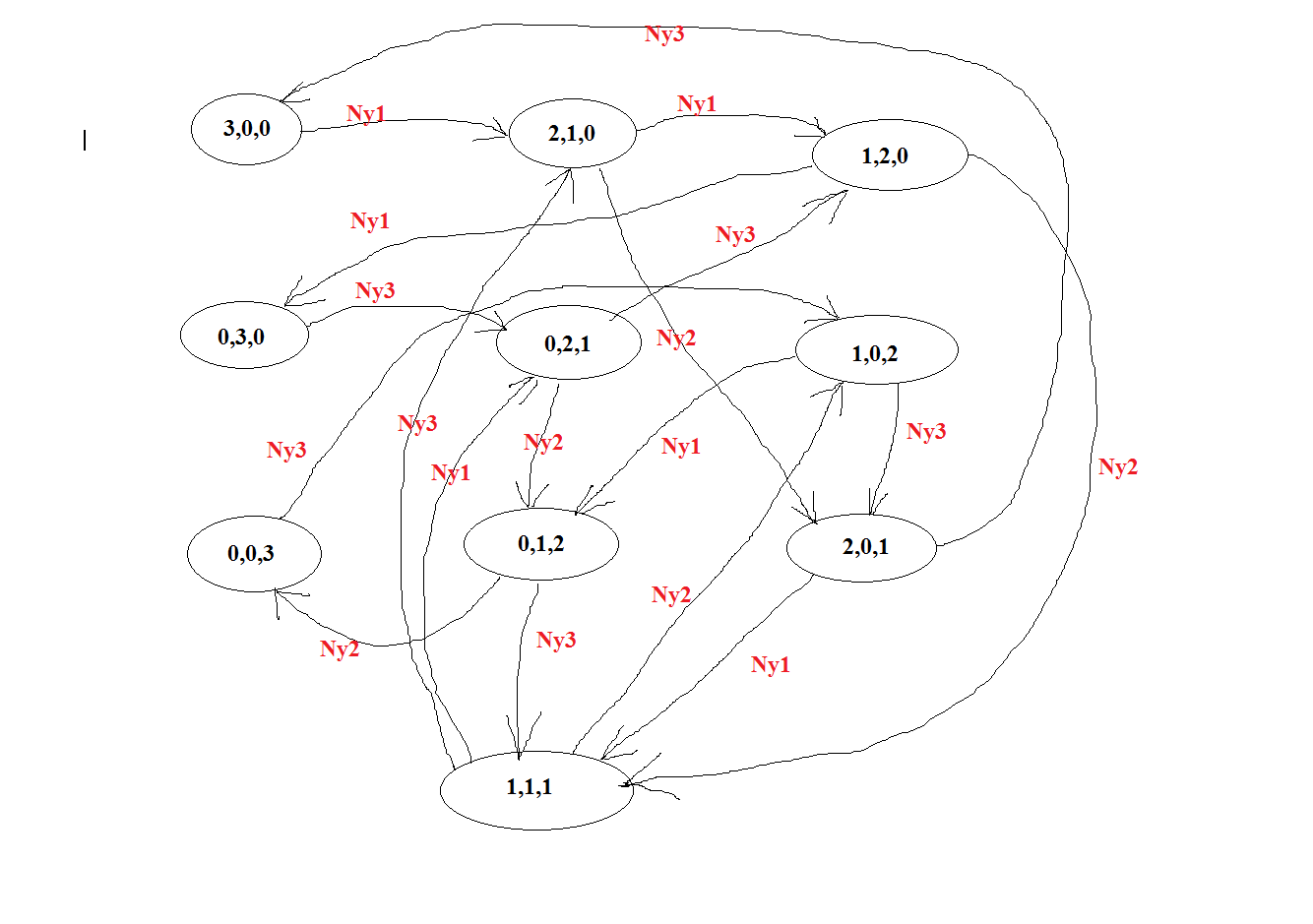




Матрица интенсивностей переходов:





Уравнение глобального баланса:

X1=π(3,0,0)=Ny3/Ny1π(2,0,1)=2.8/2.1*X10=1.33*X10=0.154
X2=π(0,3,0)=Ny1/Ny3π(1,2,0)=2.1/2.8*X8=0.75*X8=0.079
X3=π(0,0,3)=Ny2/Ny3π(0,2,1)=2.5/2.8*X5=0.892*X5=0.071
X4=π(2,1,0)=Ny1/(Ny1+Ny2)π(3,0,0)+Ny3/(Ny1+Ny2)π(1,1,1)=

2.1/(2.1+2.5)*X1+2.8/(2.1+2.5)*X7=0.456*X1+0.608*X7=0.129
X5=π(0,2,1)=Ny3/(Ny3+Ny2)π(0,3,0)+Ny1/(Ny3+Ny2)π(1,1,1)=

2.8/(2.8+2.5)*X2+2.1/(2.8+2.5)*X7=0.528*X2+0.396*X7=0.08
X6=π(0,1,2)=Ny2/(Ny3+Ny2)π(0,2,1)+Ny1/(Ny3+Ny2)π(1,2,0)=

2.5/(2.8+2.5)*X5+2.1/(2.8+2.5)*X8=0.471*X5+0.396*X8=0.079
X7=π(1,1,1)=Ny3/(Ny3+Ny2+Ny1)π(0,1,2)+Ny2/(Ny3+Ny2+Ny1)π(1,2,0)+ Ny1/(Ny3+Ny2+Ny1)π(2,0,1)=2.8/(2.1+2.5+2.8)*X6+2.5/(2.1+2.5+2.8)*X8+

2.1/(2.1+2.5+2.8)*X10=0.378*X6+0.337*X8+0.283*X10=0.098
X8=π(1,2,0)=Ny1/(Ny1+Ny2)π(2,1,0)+Ny3/(Ny1+Ny2)π(0,1,2)=

2.1/(2.1+2.5)*X4+2.8/(2.1+2.5)*X6=0.456*X4+0.608*X6=0.105
X9=π(1,0,2)=Ny3/(Ny3+Ny1)π(0,0,3)+Ny2/(Ny3+Ny1)π(1,1,1)=

2.8/(2.1+2.8)*X3+2.5/(2.1+2.8)*X7=0.571*X3+0.510*X7=0.09
X10=π(2,0,1)=Ny2/(Ny3+Ny1)π(2,1,0)+Ny3/(Ny3+Ny1)π(1,0,2)=

2.5/(2.1+2.8)*X4+2.8/(2.1+2.8)*X9=0.510*X4+0.571*X9=0.115
X1+X2+X3+X4+X5+X6+X7+X8+X9+X10=1
Маргинальные вероятности:

π₁(0)= π(0,3,0)+ π(0,0,3)+ π(0,2,1)+ π(0,1,2)=

X2+X3+X5+X6=0.079+0.071+0.08+0.079=0.3
π₁(1)= π(1,1,1)+ π(1,2,0)+ π(1,0,2)=

X7+X8+X9=0.098+0.105+0.09=0.293
π₁(2)= π(2,1,0)+π(2,0,1)=

X4+X10=0.129+0.115=0.224
π₁(3)= π(3,0,0)=X1=0.154
π₂(0)= π(3,0,0)+π(0,0,3)+π(1,0,2)+π(2,0,1)=

X1+X3+X9+X10=0.154+0.071+0.09+0.115=0.43
π₂(1)= π(2,1,0)+π(0,1,2)+π(1,1,1)=

X4+X6+X7=0.129+0.079+0.098=0.306
π₂(2)= π(0,2,1)+π(1,2,0)=

X5+X8=0.08+0.105=0.185
π₂(3)= π(0,3,0)=X2=0.079
π₃(0)= π(3,0,0)+π(0,3,0)+π(2,1,0)+π(1,2,0)=

X1+X2+X4+X8=0.154+0.079+0.129+0.105=0.47
π₃(1)= π(0,2,1)+π(1,1,1)+π(2,0,1)=

X5+X7+X4=0.08+0.098+0.129=0.307
π₃(2)= π(0,1,2)+π(1,0,2)=

X6+X9=0.079+0.09=0.169
π₃(3)= π(0,0,3)=X3=0.071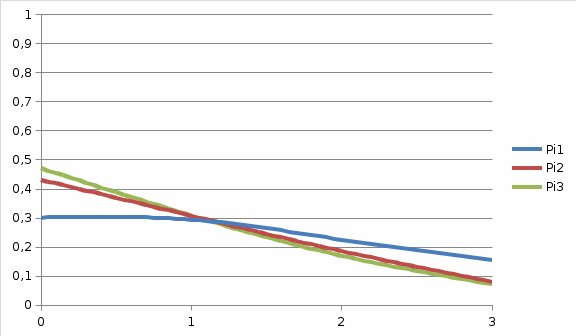




Рисунок 2 – График зависимости маргинальных вероятностей от состояний узлов

Коэффициенты загрузки:

δ1=1-π₁(0)=1-0.3=0.7
δ2=1-π₂(0)=1-0.43=0.57
δ3=1-π₃(0)=1-0.47=0.53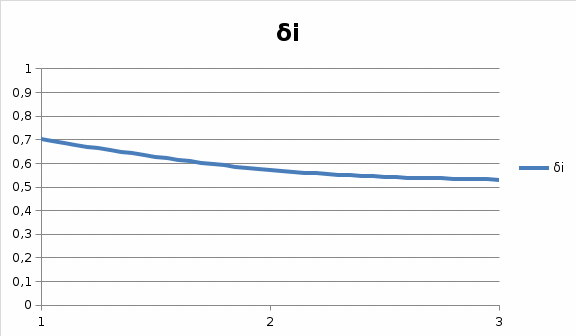




Рисунок 3 – График зависимости коэффициента загрузки от номера узла

Интенсивности:

γ1= δ1*µ1*m1=0.7*2.1*2=2.94
γ2= δ2*µ2*m2=0.57*2.5*3=4.27
γ3= δ3*µ3*m3=0.53*2.8*3=4.47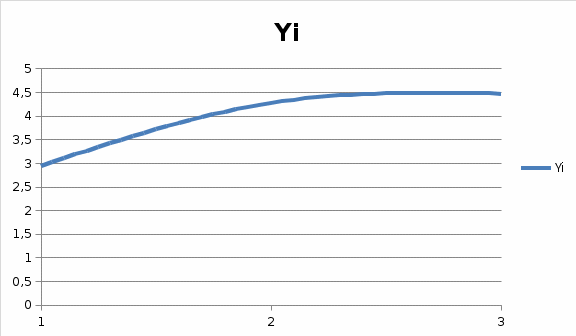


Рисунок 4 – График зависимости интенсивностей входящих потоков заявок от номера узла

Количество заявок:

K1= 1* π₁(1) + 2* π₁(2) + 3* π₁(3) =0.293+2*0.244+3*0.154=1.24
K2= 1* π₂(1) + 2* π₂(2) + 3* π₂(3) =0.306+2*0.185+3*0.079=0.91
K3= 1* π₃(1) + 2* π₃(2) + 3* π₃(3) =0.307+2*0.169+3*0.071=0.85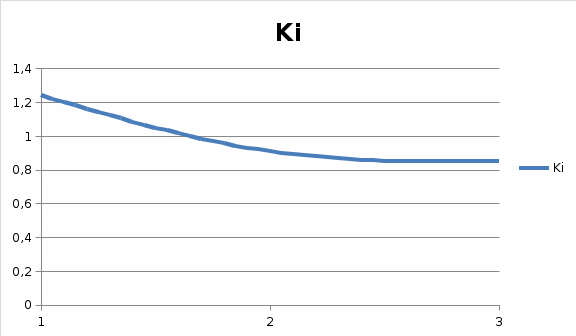



Рисунок 5 – График зависимости среднего числа заявок от номера узла

Проверка:

K = K1 + K2 + K3 =1.24+0.91+0.85=3
Среднее время реакции:

T1 = K1/λ1 = 1.24/2.94=0.42

T2 = K2/λ2 = 0.91/4.27=0.21

T3 = K3/λ3 = 0.85/4.47=0.19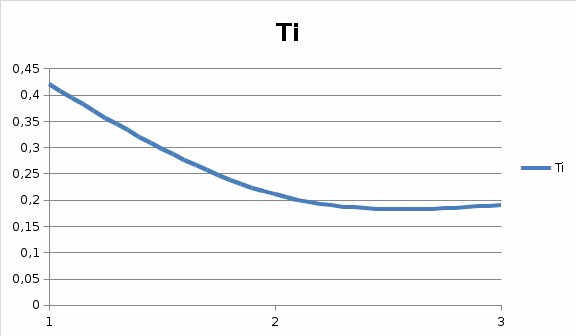



Рисунок 6 – График зависимости среднего времени реакции от номера узла

Время ожидания:

W1 = T1 – 1/μ1 = 0.42-1/2.1= -0.05

W2 = T2 – 1/μ2 = 0.21-1/2.5= -0.19

W3 = T3 – 1/μ3 =0.19-1/2.8= -0.16
Средняя длина очереди в узлах
Q1= λ1*W1=2.94*-0.05= -0.15
Q2= λ2*W2=4.27*-0.19= -0.81
Q3= λ3*W3=4.47*-0.16= -0.71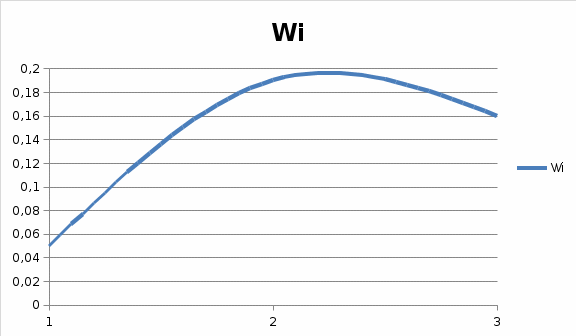




Рисунок 7 – График зависимости времени ожидания от номера узла (по модулю)

Номер узла	1	2	3
Коэффициенты переходов, e	1	1,029	1,214
Относительный коэффициент загрузки узлов, b	0.476	0.411	0.434
Маргинальные вероятности	π1(0)=0.3 π1(1)=0.293 π1(2)=0.224 π1(3)=0.154	π2(0)=0.43 π2(1)=0.306 π2(2)=0.185 π2(3)=0.079	π3(0)=0.47 π3(1)=0.307 π3(2)=0.169 π3(3)=0.071
Коэффициенты загрузки, ρ	0.7	0.57	0.53
Интенсивности входящих потоков заявок	2.94	4.27	4.47
Количество заявок, K	1.24	0.91	0.85
Среднее время реакции, T	0.42	0.21	0.19
Время ожидания, W	-0.05	-0.19	-0.16
Средняя длина очереди, Q	-0.15	-0.81	-0.71

Вывод по работе:

В ходе выполнения лабораторной работы мы научились составлять и решать системы уравнений глобального баланса для анализа замкнутых однородных марковских СеМО, а также применять результаты расчёта для вычисления узловых и сетевых характеристик СеМО.

Контрольные вопросы: