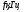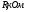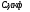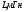лаба. лаба 1. Лабораторная работа 1. Применение принципа наложения (принципа суперпозиции) для определения реакции линейной цепи на произвольное периодическое воздействие
 Скачать 1.46 Mb.
|
 Лабораторная работа №1.Применение принципа наложения (принципа суперпозиции) для определения реакции линейной цепи на произвольное периодическое воздействие Цель работы:получить навыки применения принципа наложения (принципа суперпозиции) для определения реакции линейной цепи на произвольное периодическое воздействие. Задание. Определить реакцию линейной электрической цепи, представленной на рисунке 1, на внешнее периодическое воздействие, форма которого представлена в таблице 1. Сравнить найденную аналитическим путем реакцию цепи с осциллограммой, полученной в программе электронного моделирования NIMultisim. 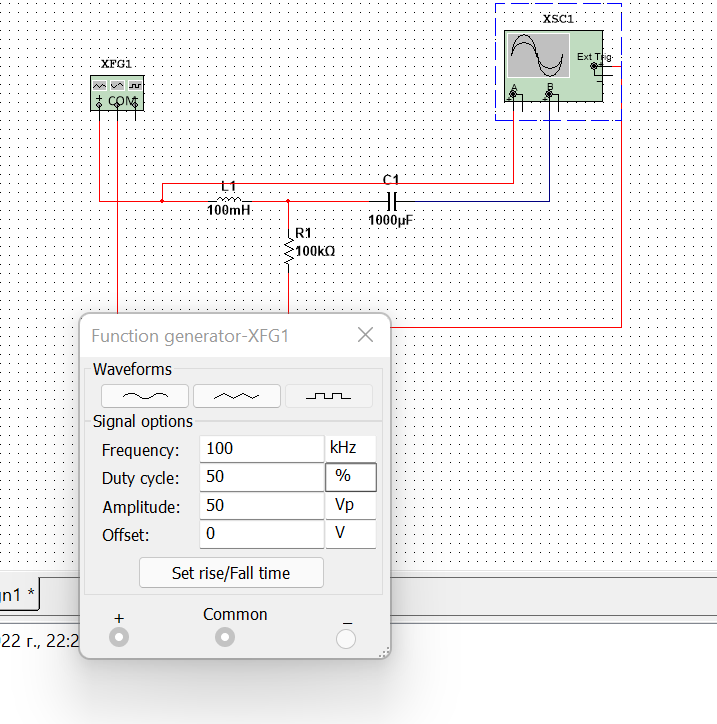 Рисунок 1 – исследуемая линейная электрическая цепь Таблица 1 – исходные данные
Ход работы: Представим входной сигнал в аналитическом виде, опираясь на осциллограмму входного сигнала (рисунок 2): 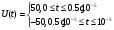 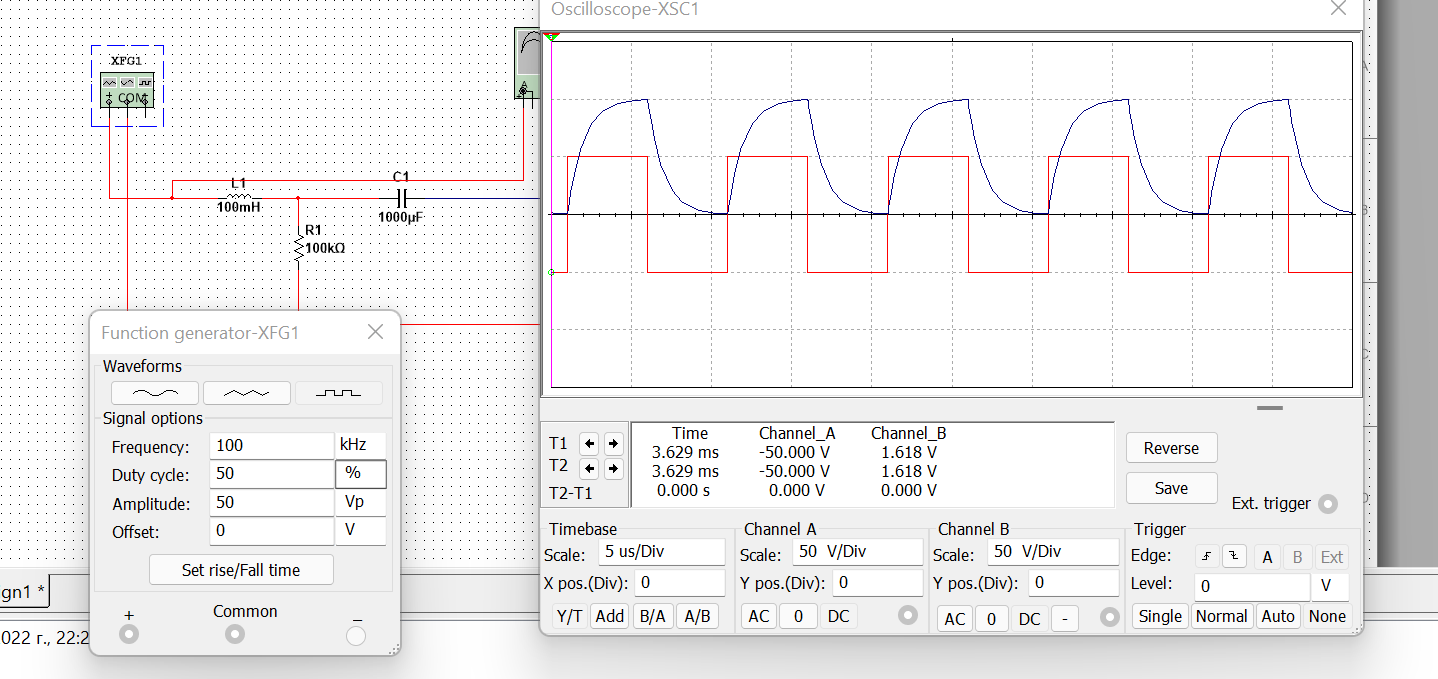 Рисунок 2 – осциллограмма входного и выходного сигналов Представим внешнее воздействие в виде тригонометрического ряда Фурье: 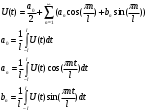 Так как на участке 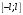 осциллограмма входного сигнала представляет собой нечетную функцию, то для нее при разложении в ряд Фурье справедливы равенства: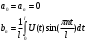 Найдем 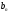 : 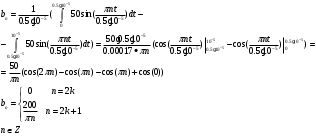Запишем разложенную в ряд Фурье функцию входного сигнала и построим ее график (с 2 по 12 гармонику) в программе электронного моделирования Mathcad (рисунок 3): 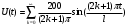 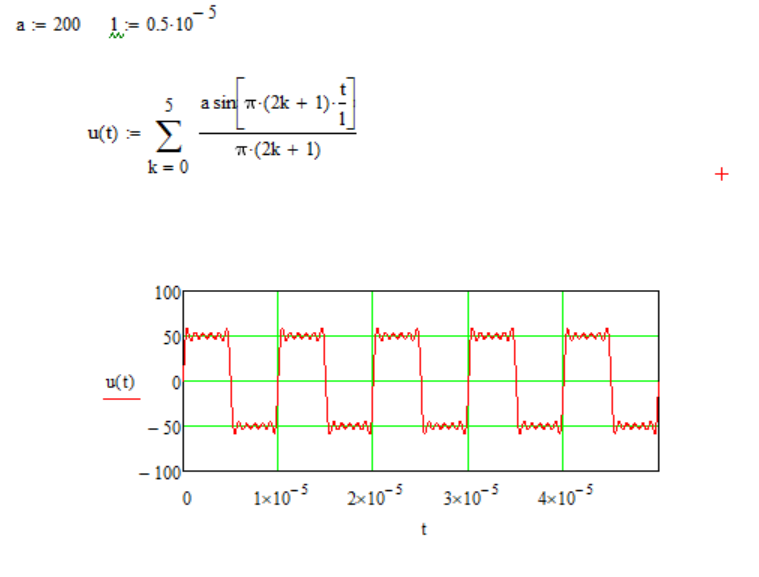 Рисунок 3 – график внешнего воздействия с 1 по 11 гармонику Используя принцип наложения, найдем реакцию исследуемой цепи на отдельные гармоники внешнего воздействия. Для первой гармоники: 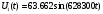 Амплитуда сигнала: 63.662B; Частота: 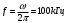 Амплитуда выходного сигнала: 53.572B; Величина фазового сдвига: 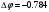 Выражение для реакции цепи на входное воздействие (рисунки 5-6): 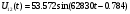 Аналогичные действия проведем для остальных гармоник и сведем полученные значения в таблицу 2, все необходимые действия в программе Mathcadпоказаны на рисунке 4.
 Рисунок 4 – данные для построения графиков в Mathcad 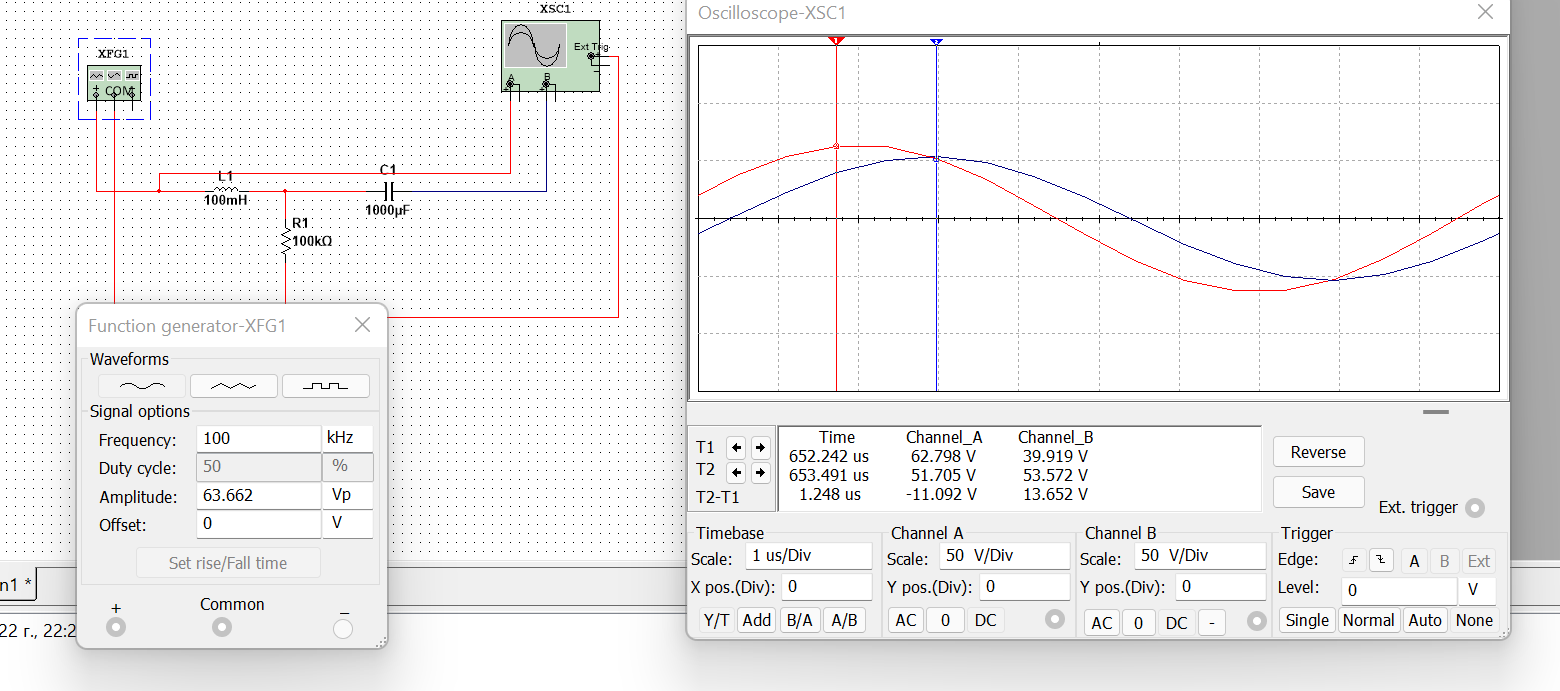 Рисунок 5 – осциллограммы первой гармоники и реакции цепи на нее 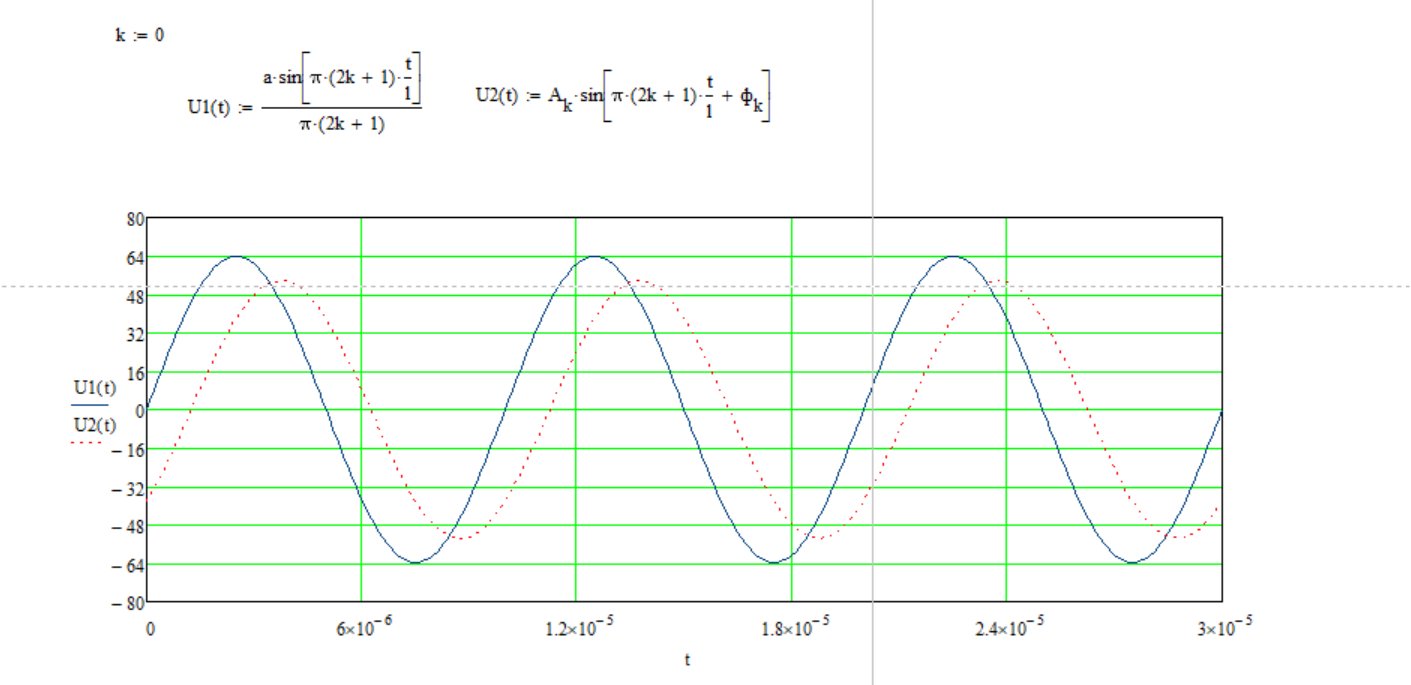 Рисунок 6 – осциллограммы первой гармоники и реакции цепи на нее, построенные в программе Mathcad 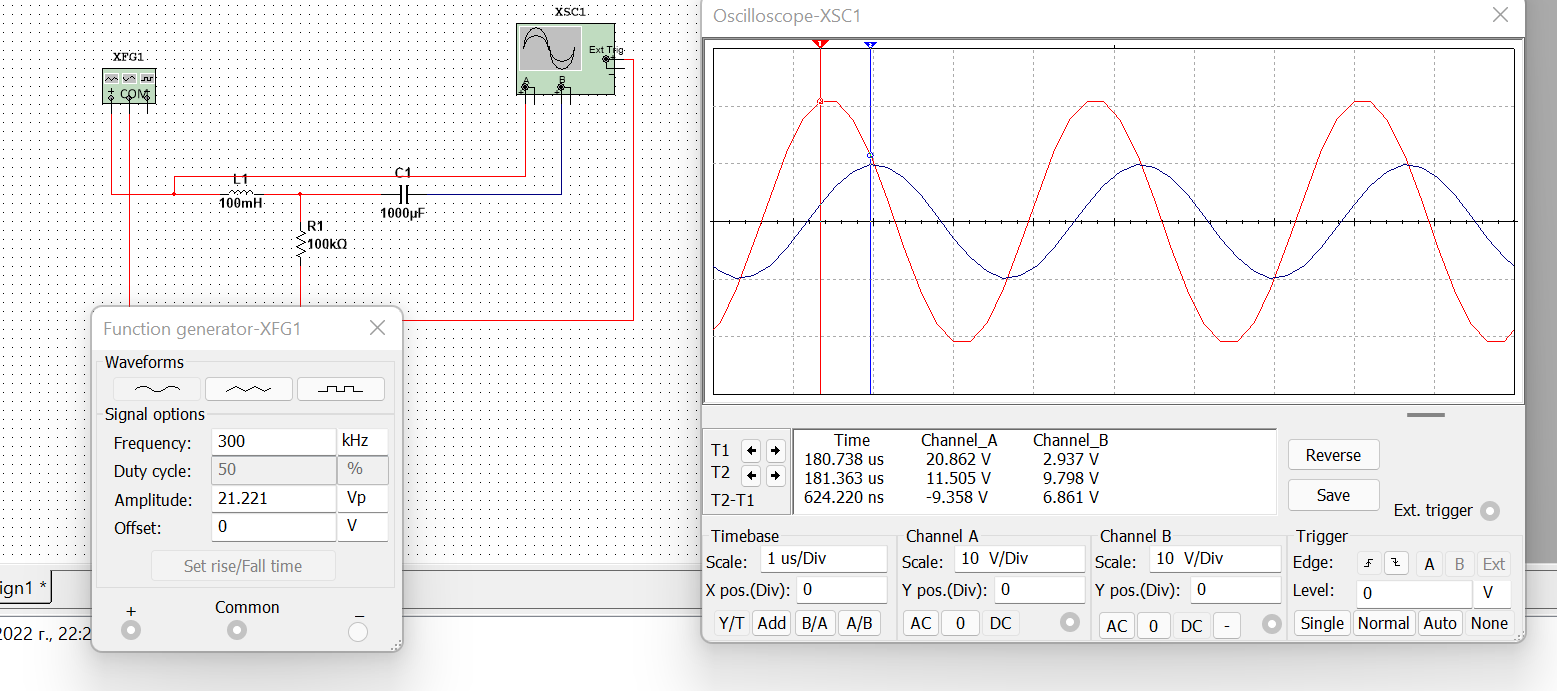 Рисунок 7 – осциллограммы третьей гармоники и реакции цепи на нее 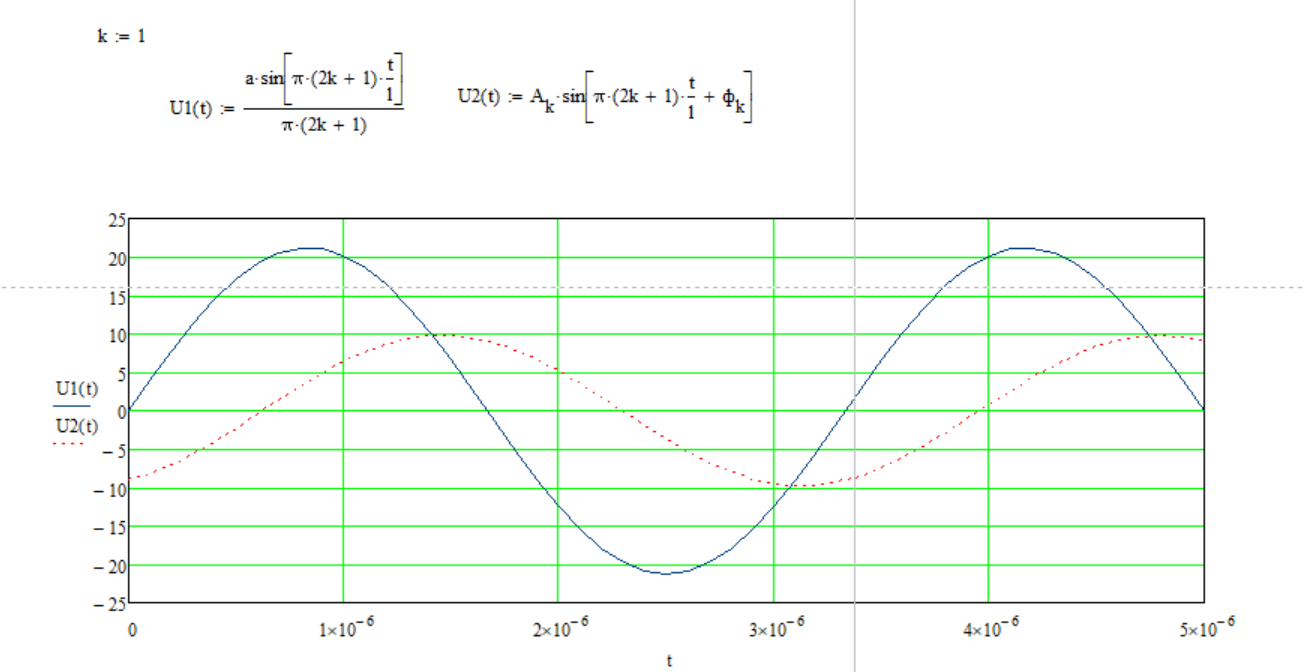 Рисунок 8 – осциллограммы третьей гармоники и реакции цепи на нее, построенные в программе Mathcad 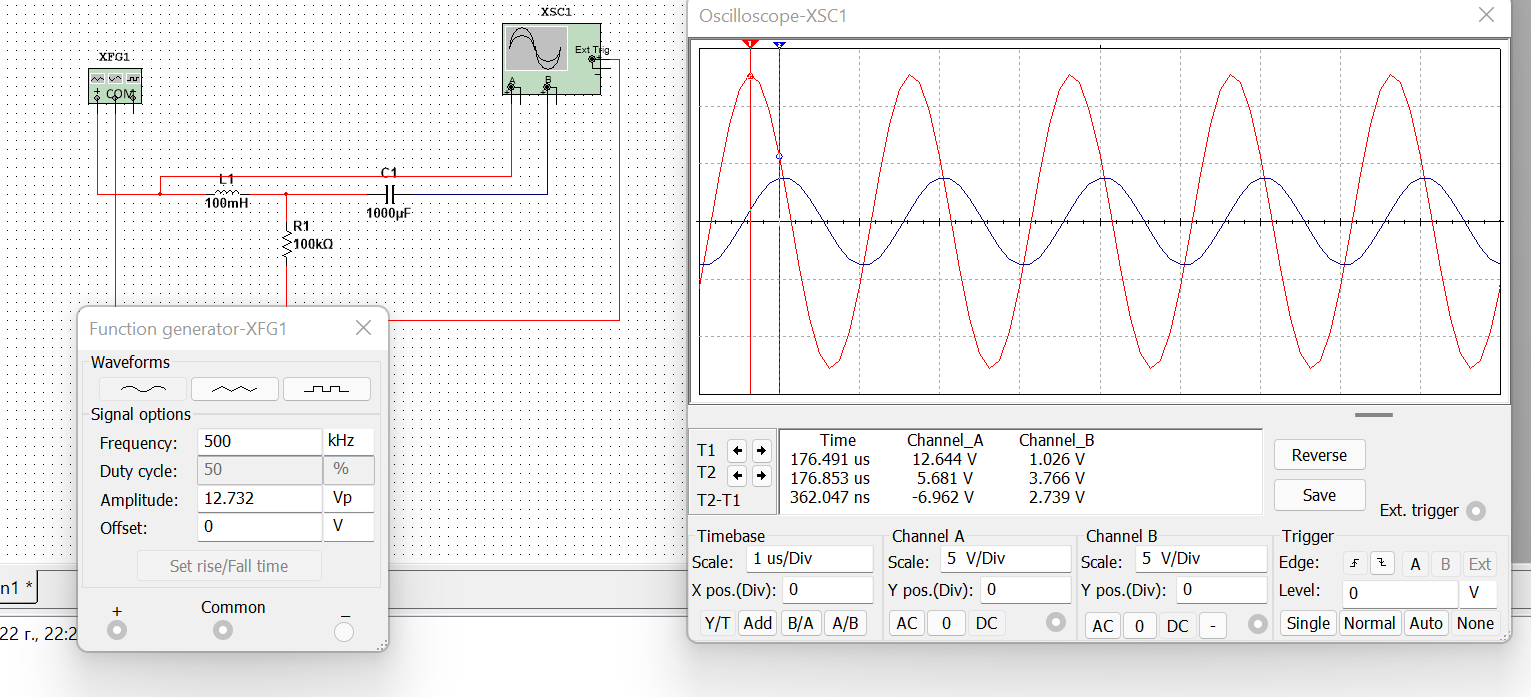 Рисунок 9 – осциллограммы пятой гармоники и реакции цепи на нее 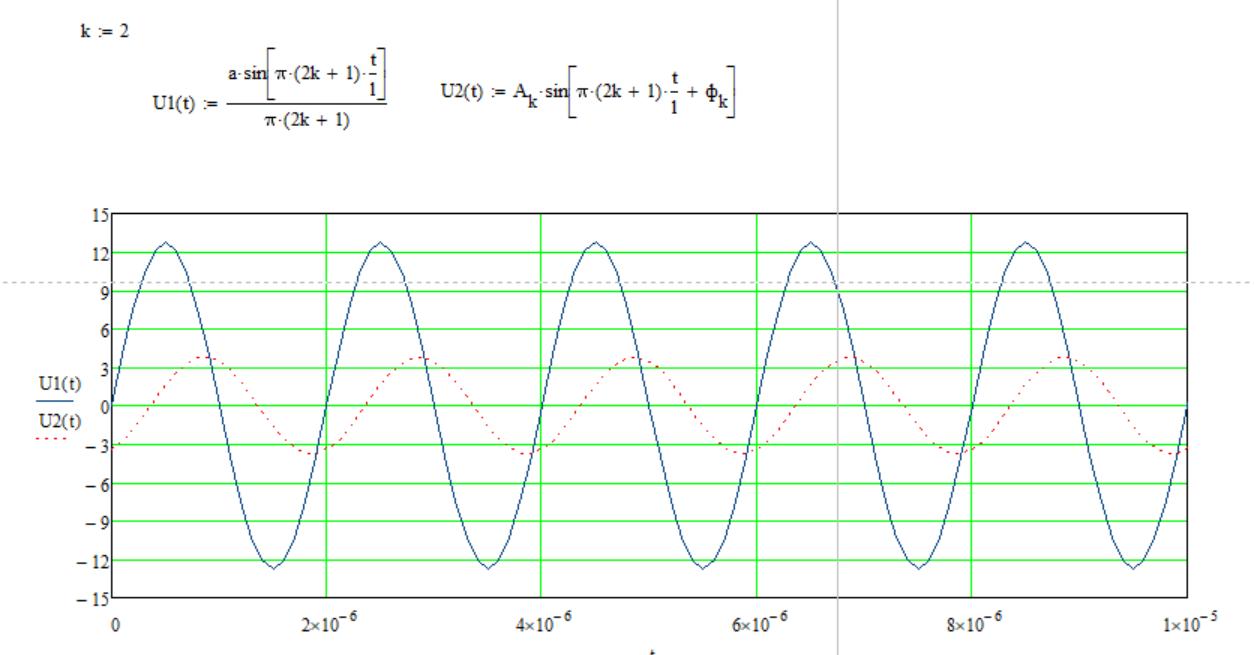 Рисунок 10 – осциллограммы пятой гармоники и реакции цепи на нее, построенные в программе Mathcad 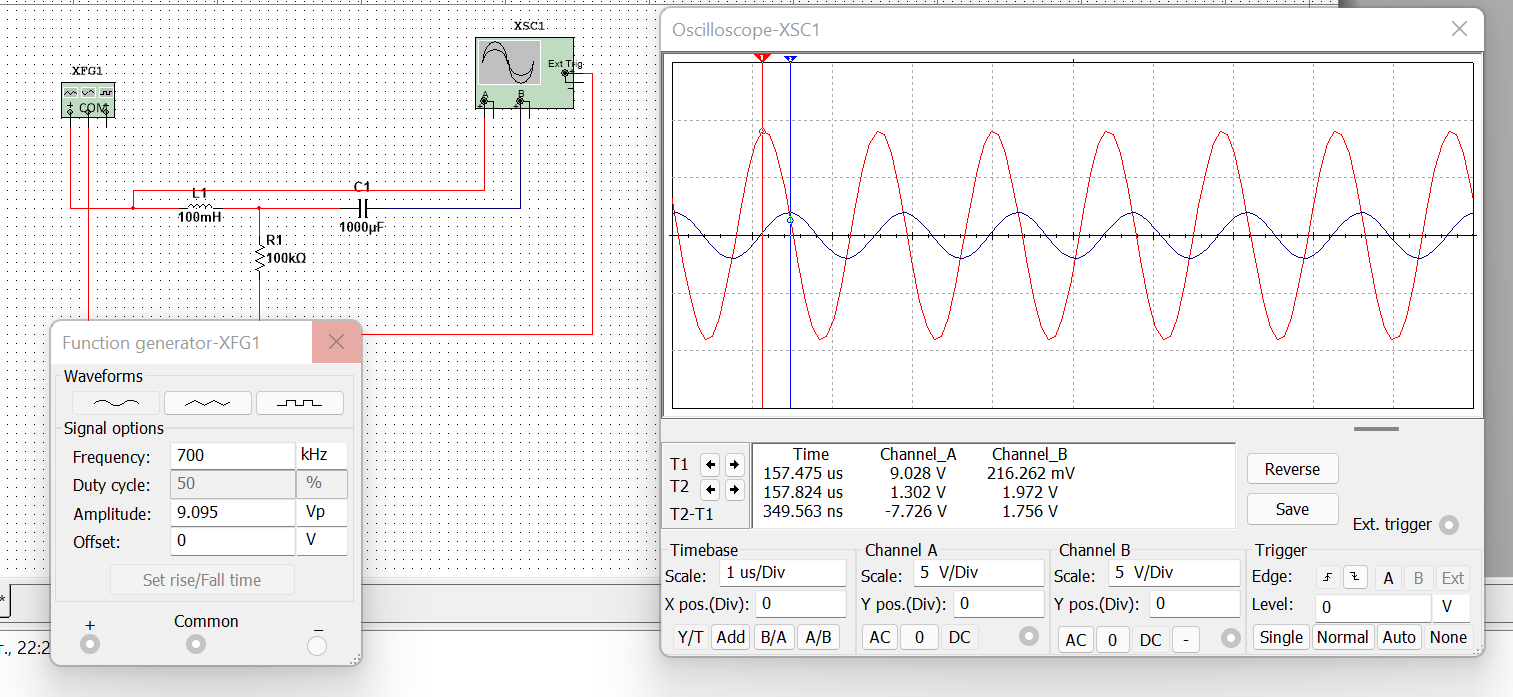 Рисунок 11 – осциллограммы седьмой гармоники и реакции цепи на нее 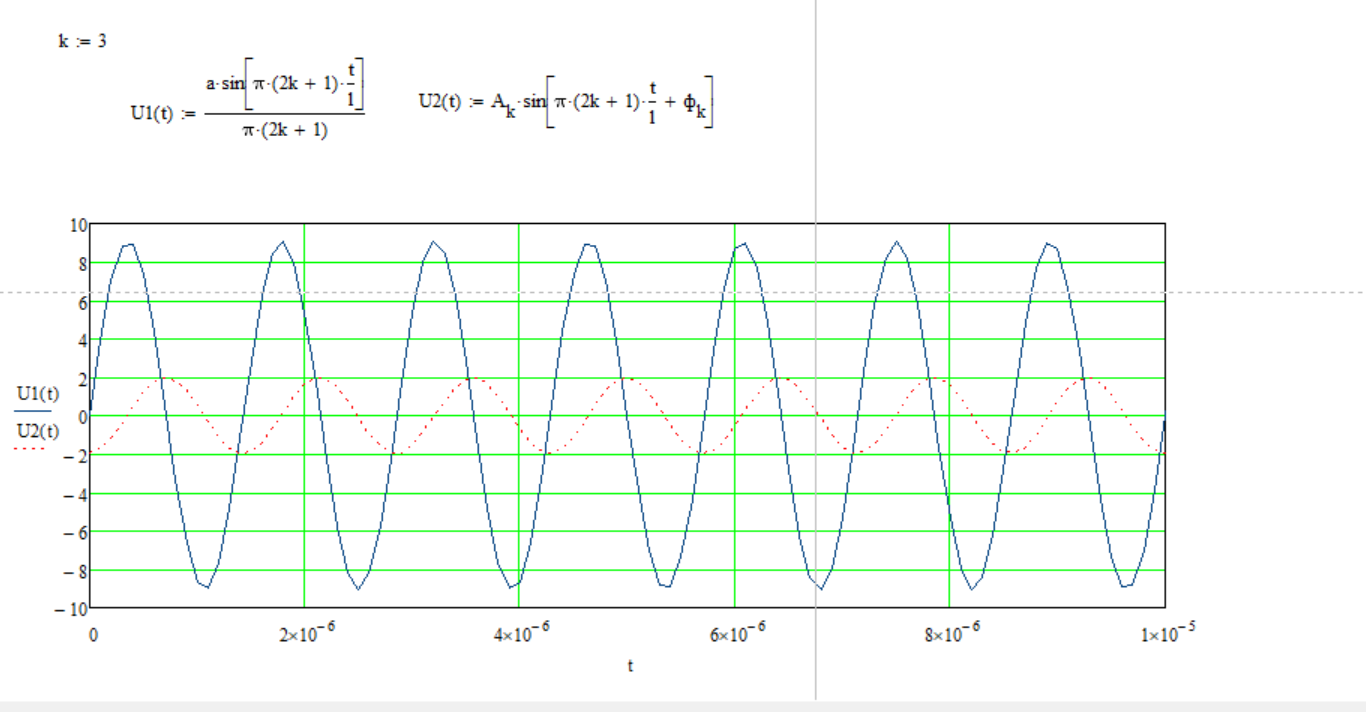 Рисунок 12 – осциллограммы седьмой гармоники и реакции цепи на нее, построенные в программе Mathcad 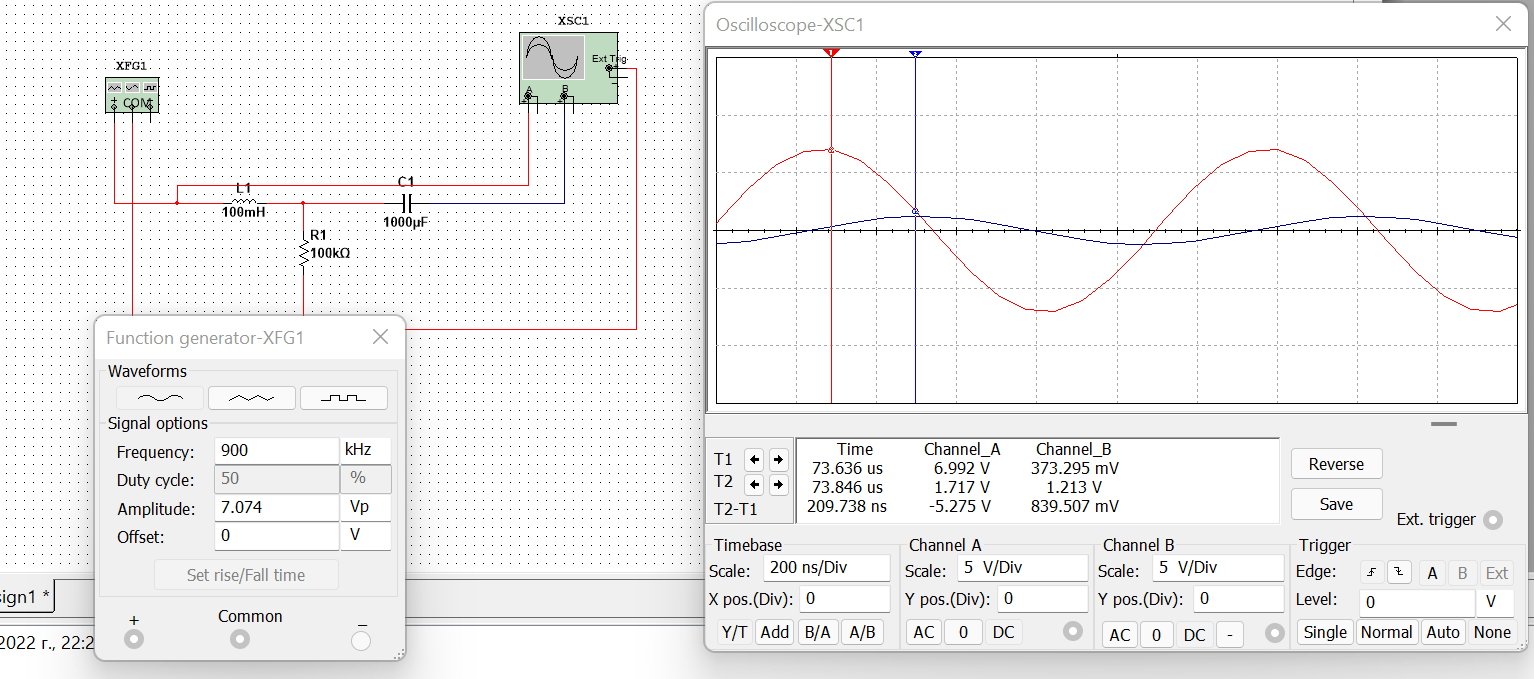 Рисунок 13 – осциллограммы девятой гармоники и реакции цепи на нее 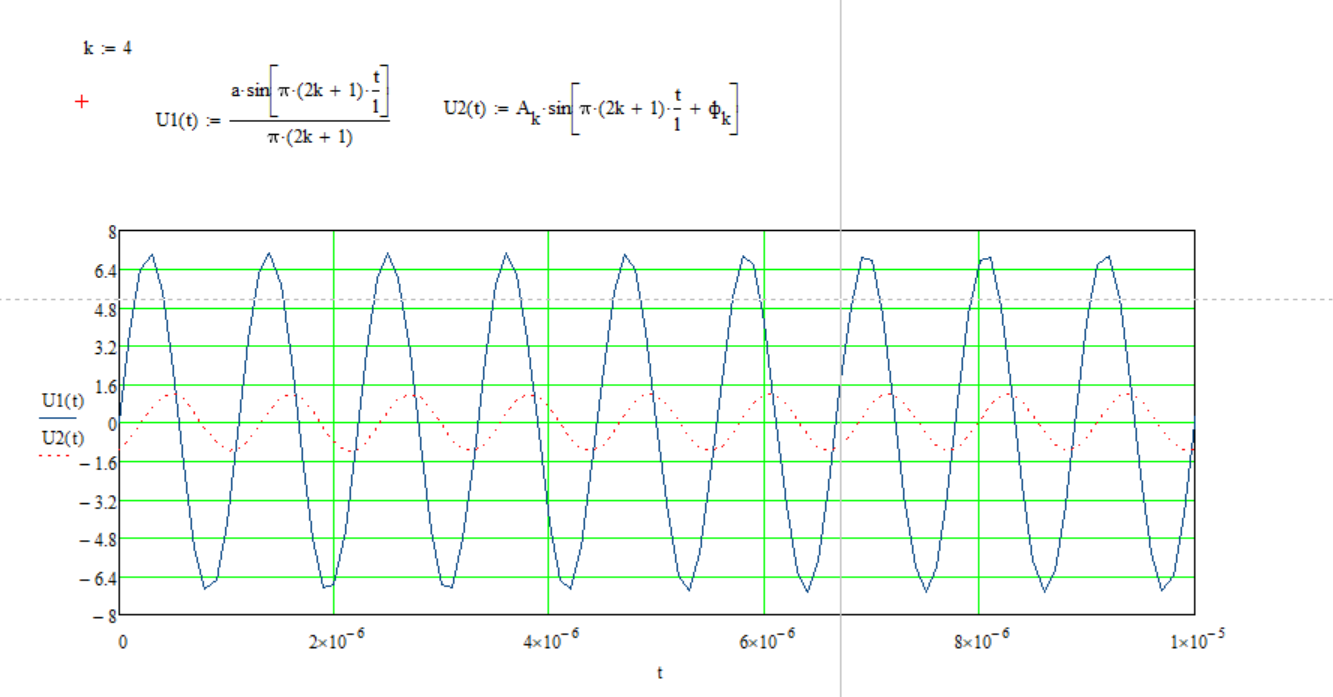 Рисунок 14 – осциллограммы девятой гармоники и реакции цепи на нее, построенные в программе Mathcad 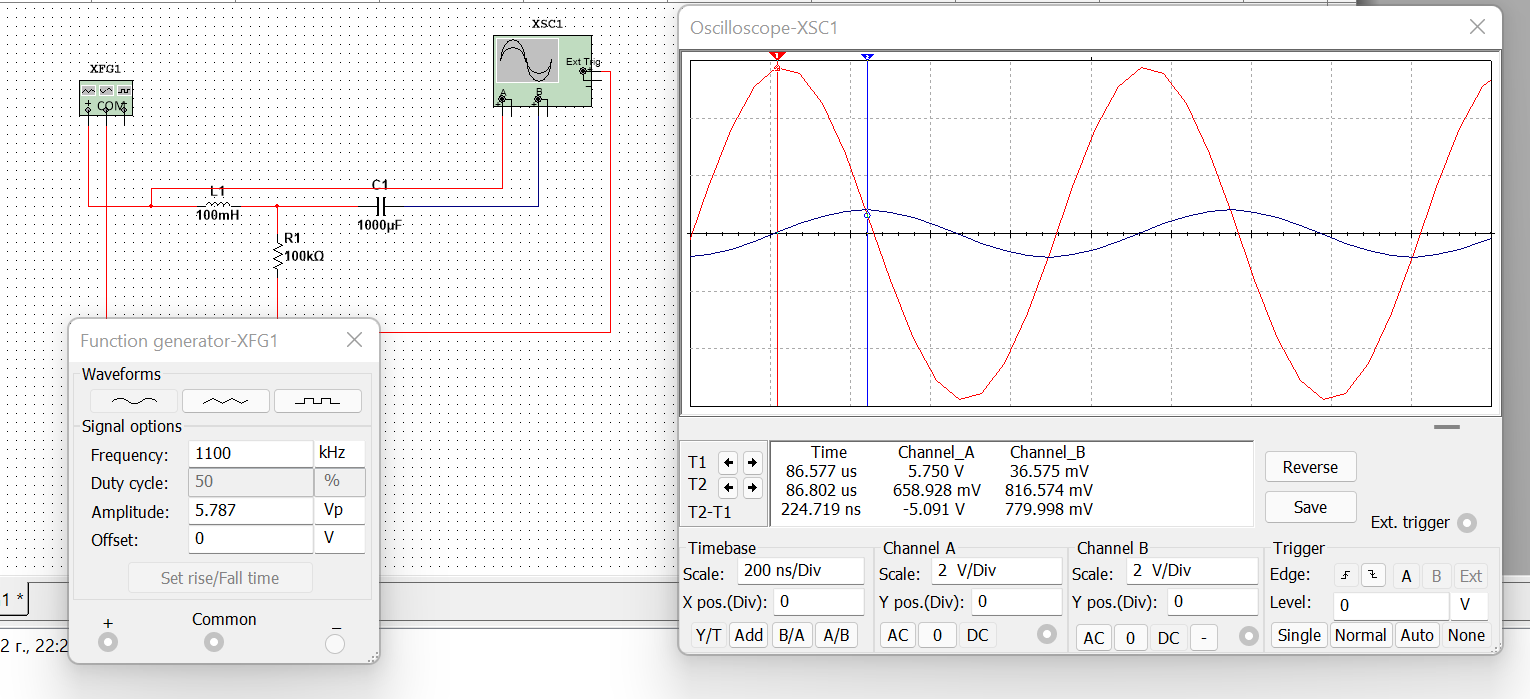 Рисунок 15 – осциллограммы одиннадцатой гармоники и реакции цепи на нее 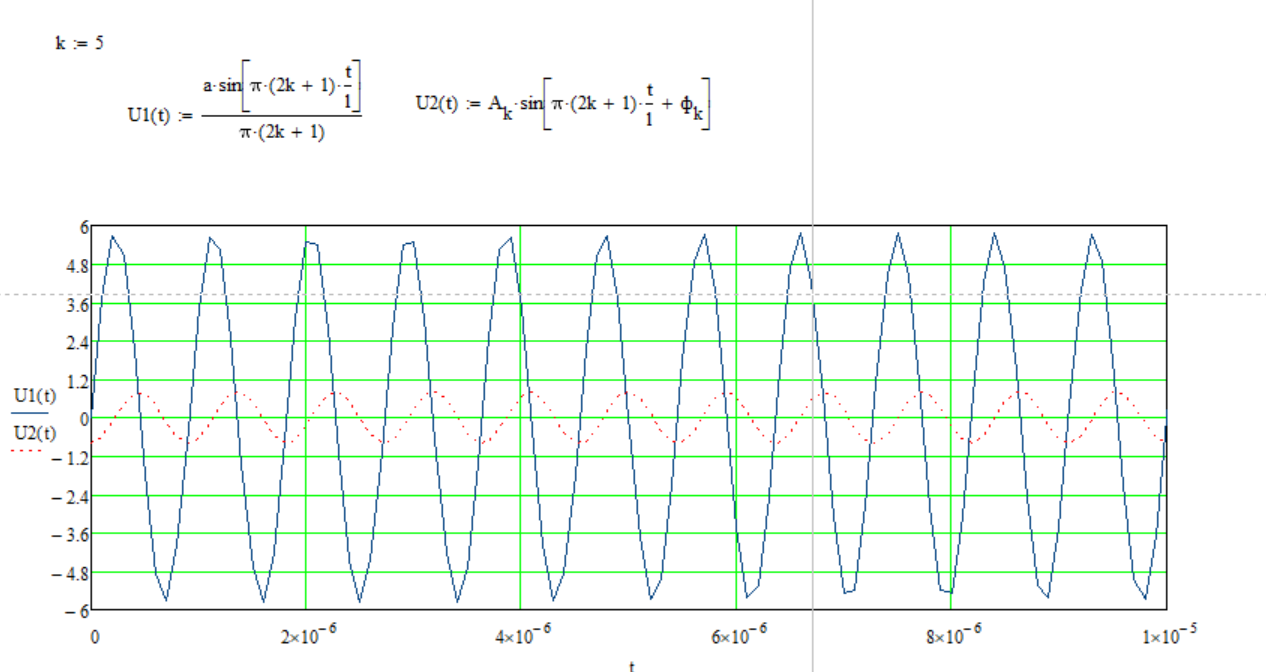 Рисунок 16 – осциллограммы 11-ой гармоники и реакции цепи на нее, построенные в программе Mathcad Получив первые 11 гармоник, согласно принципу наложения, можно построить реакцию исследуемой цепи на внешнее воздействие в программе Mathcadи сравнить полученный график с показаниями осциллографа (рисунки 17-18) 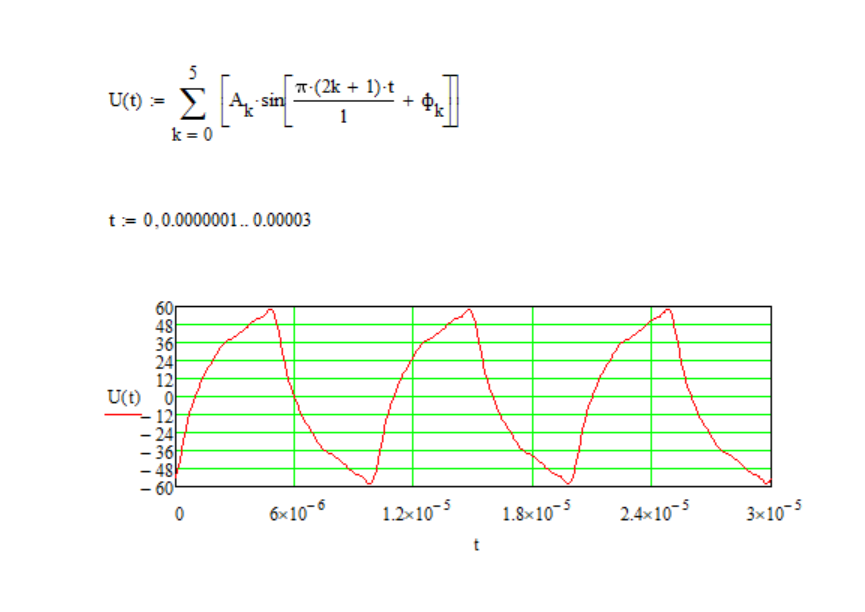 Рисунок 17 –реакция исследуемой цепи на внешнее воздействие, построенная в программе Mathcad 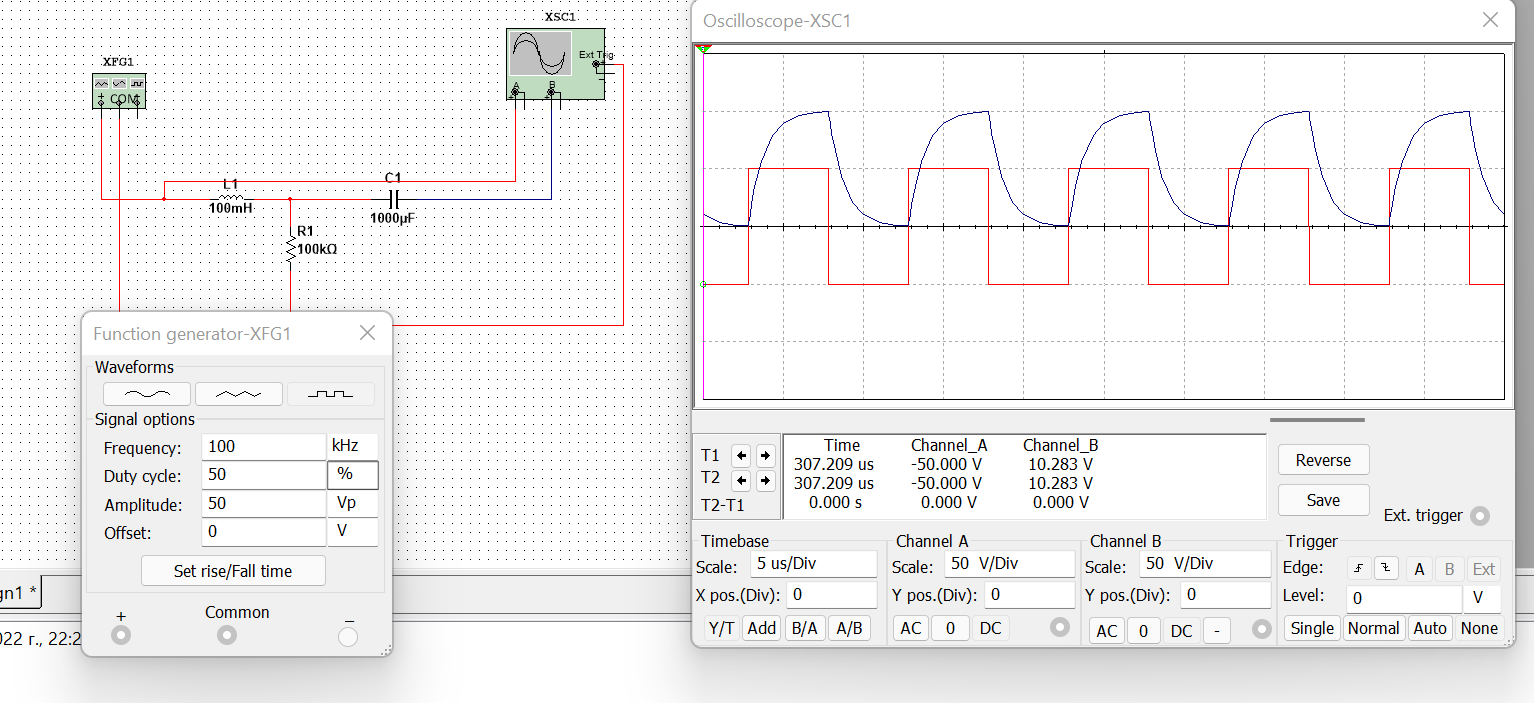 Рисунок 17 – реакция исследуемой цепи на внешнее воздействие, снятая с осциллографа в программе NIMultisim Вывод:в ходе лабораторной работы мы получили навыки применения принципа наложения (принципа суперпозиции) для определения реакции линейной цепи на произвольное периодическое воздействие. |
