|
|
Лабораторная работа 1 Теория погрешностей и машинная арифметика
ЛАБОРАТОРНАЯ РАБОТА №3
Решение систем линейных алгебраических уравнений (СЛАУ)
Практическая часть
Задание 1. Решить СЛАУ (систему линейных алгебраических уравнений), Ax=b, методом Гаусса или Жордана-Гаусса, предварительно исследовать совместность этих уравнений.
Вариант 1
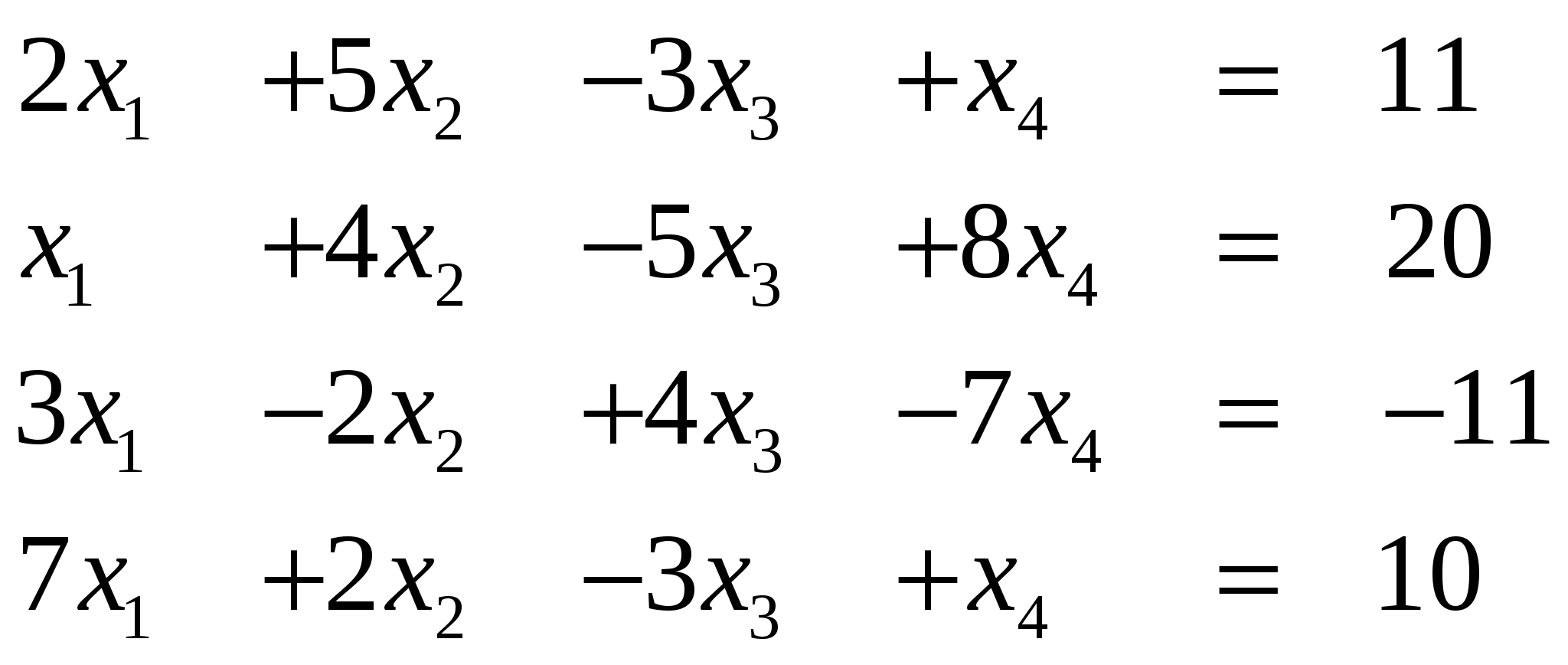
Ответ (1; …)
|
Вариант 2
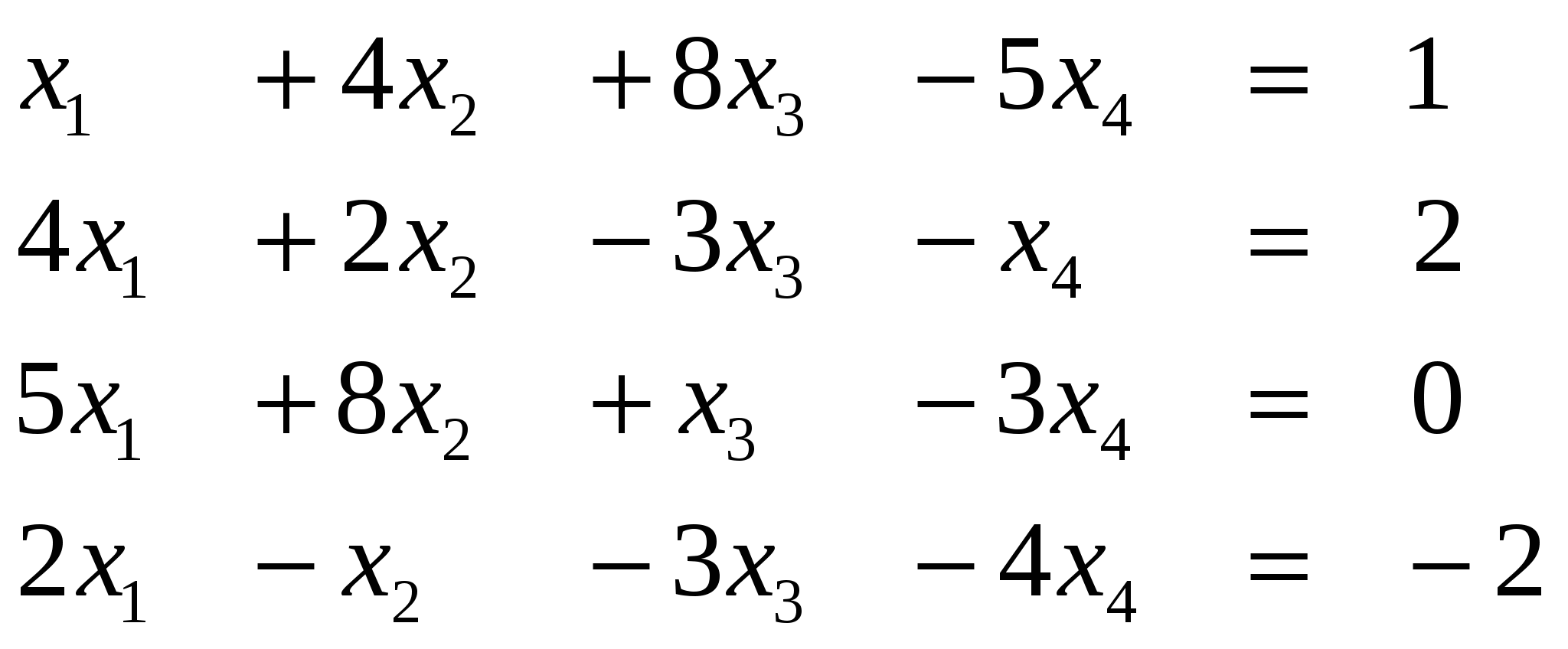
Ответ (2; …)
|
Вариант 3
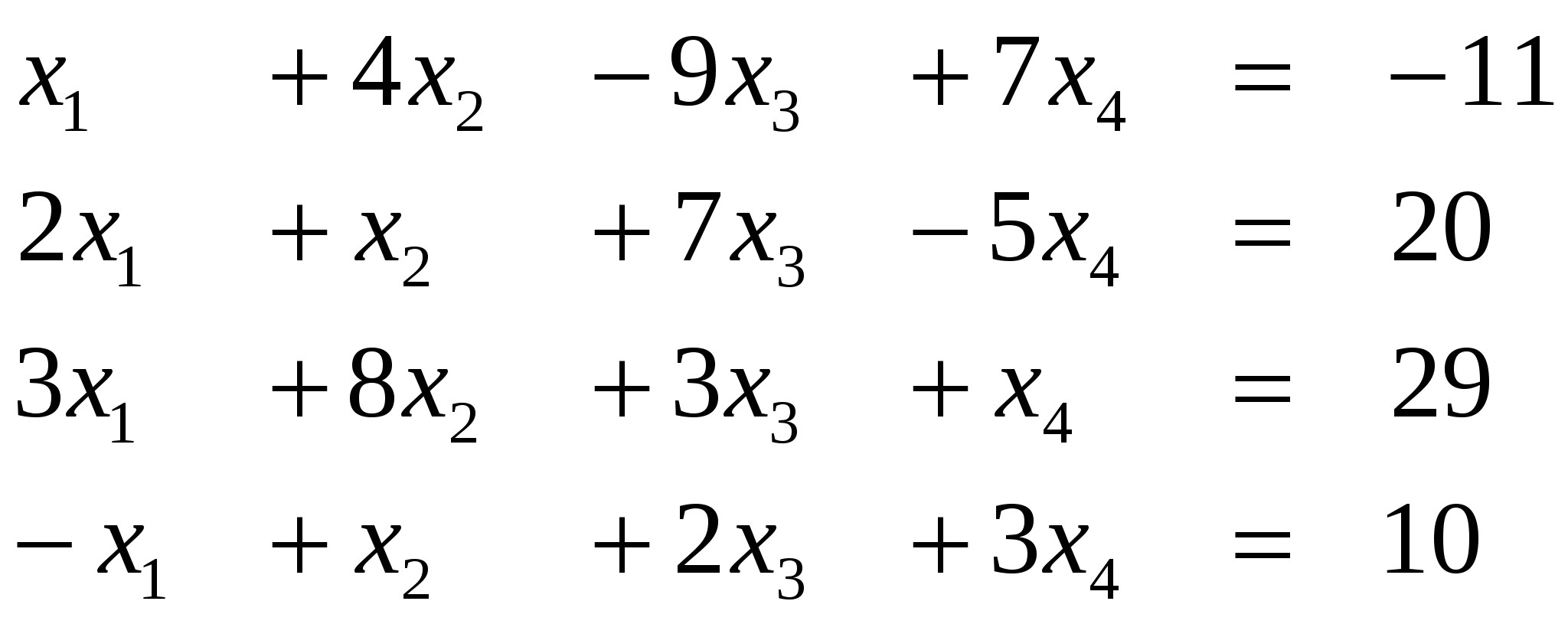
Ответ (1; …)
|
Вариант 4
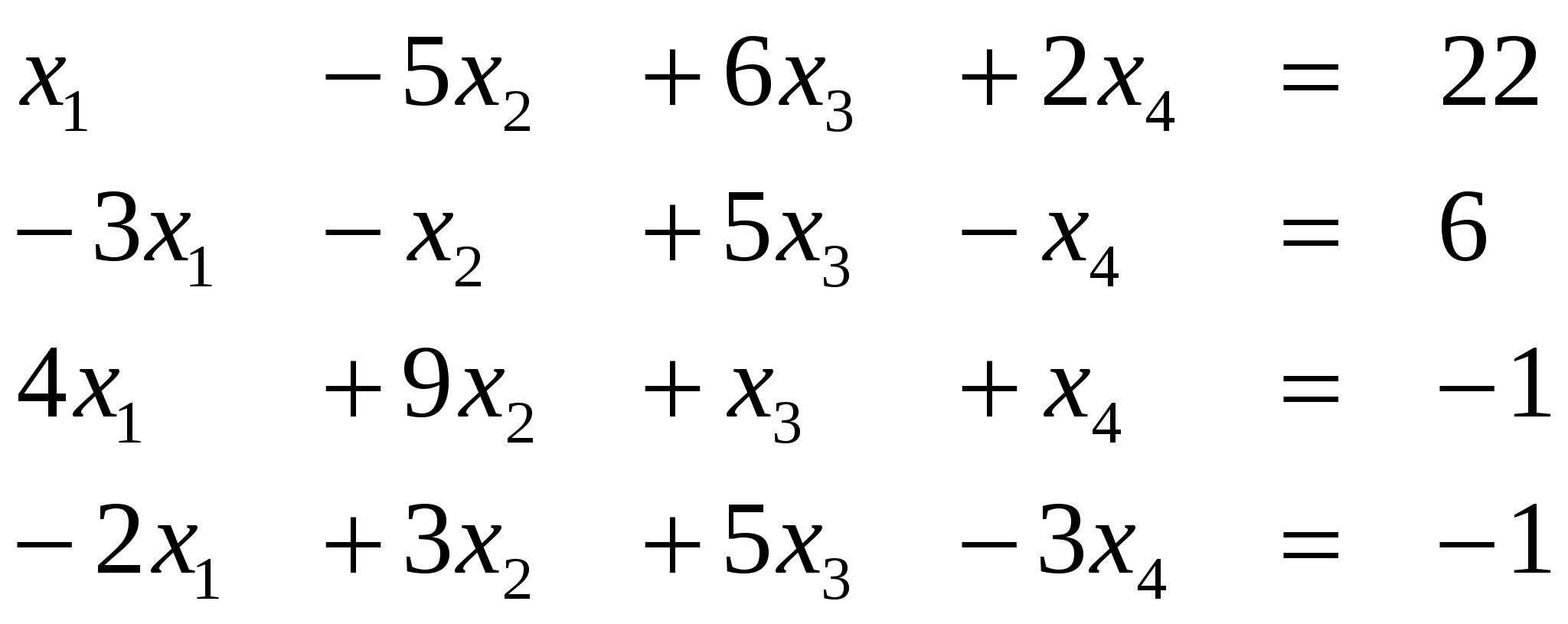
Ответ (1; …)
|
Вариант 5
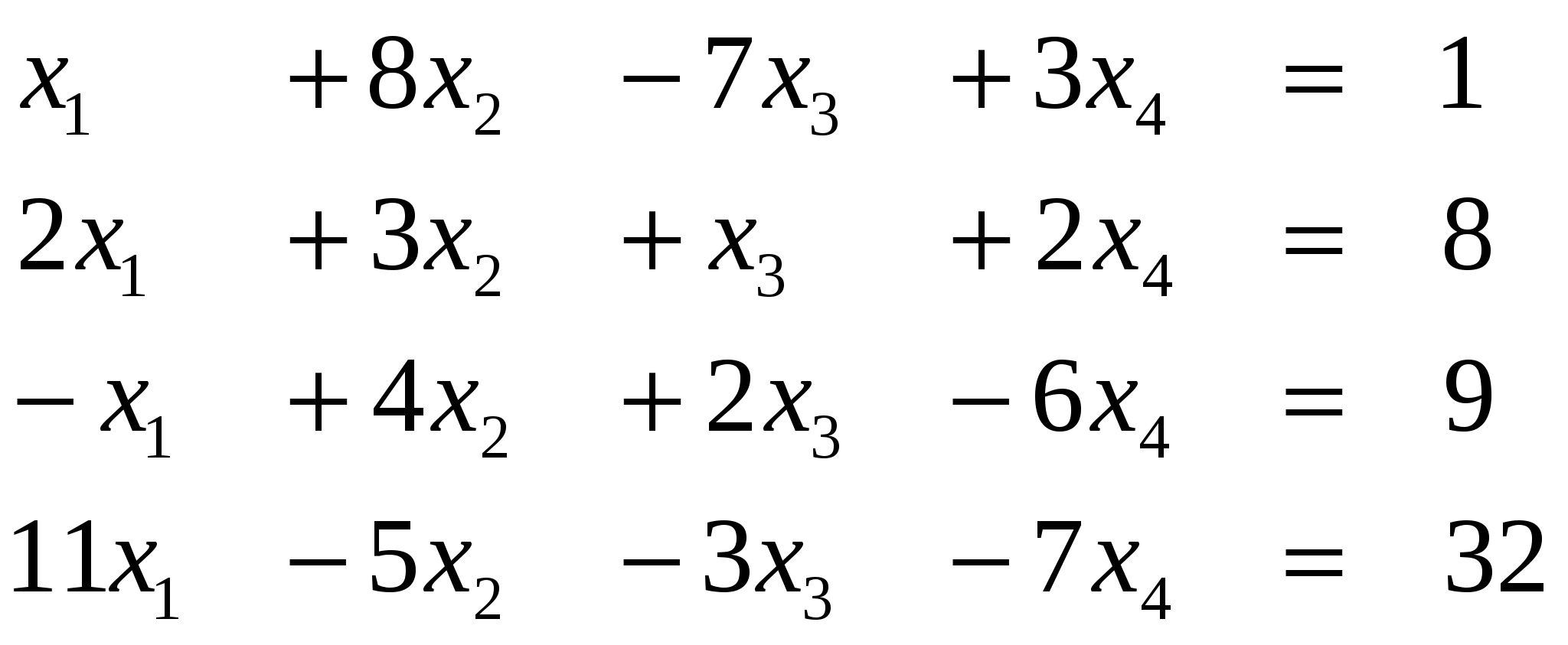
Ответ (3; ….)
|
Вариант 6
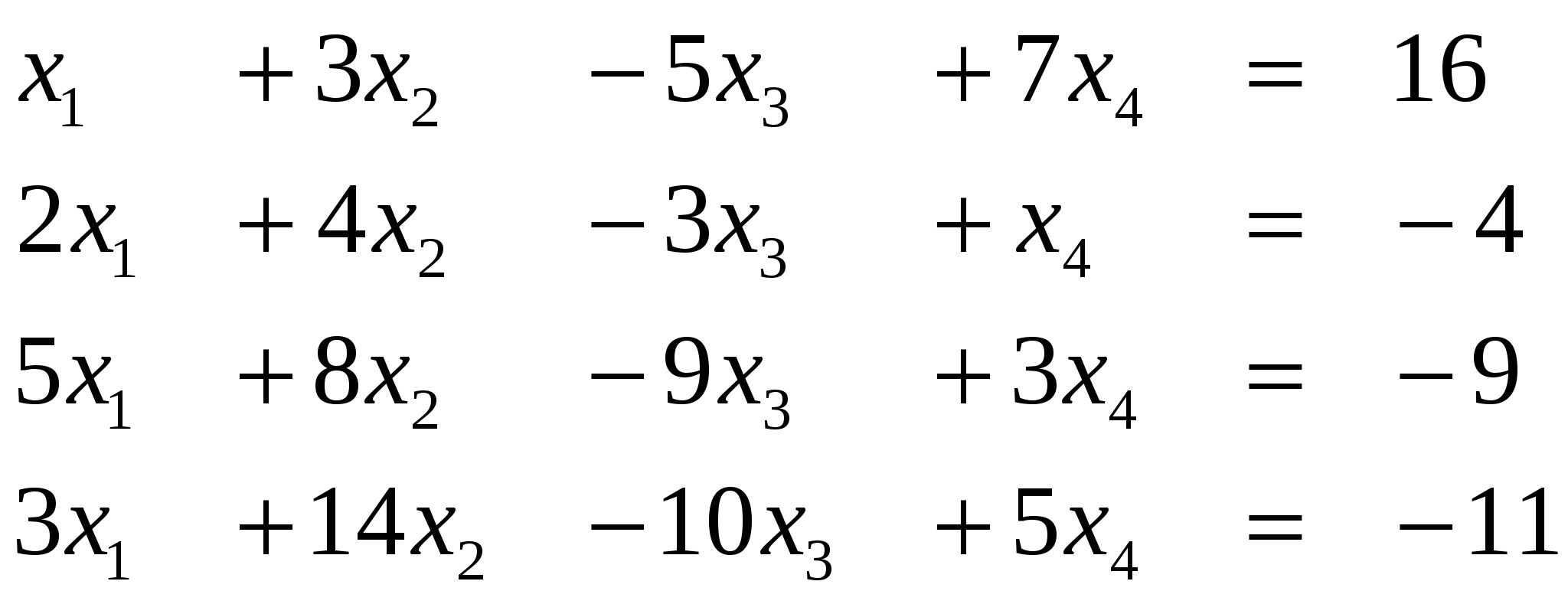 Ответ (1; ….) Ответ (1; ….)
|
Вариант 7
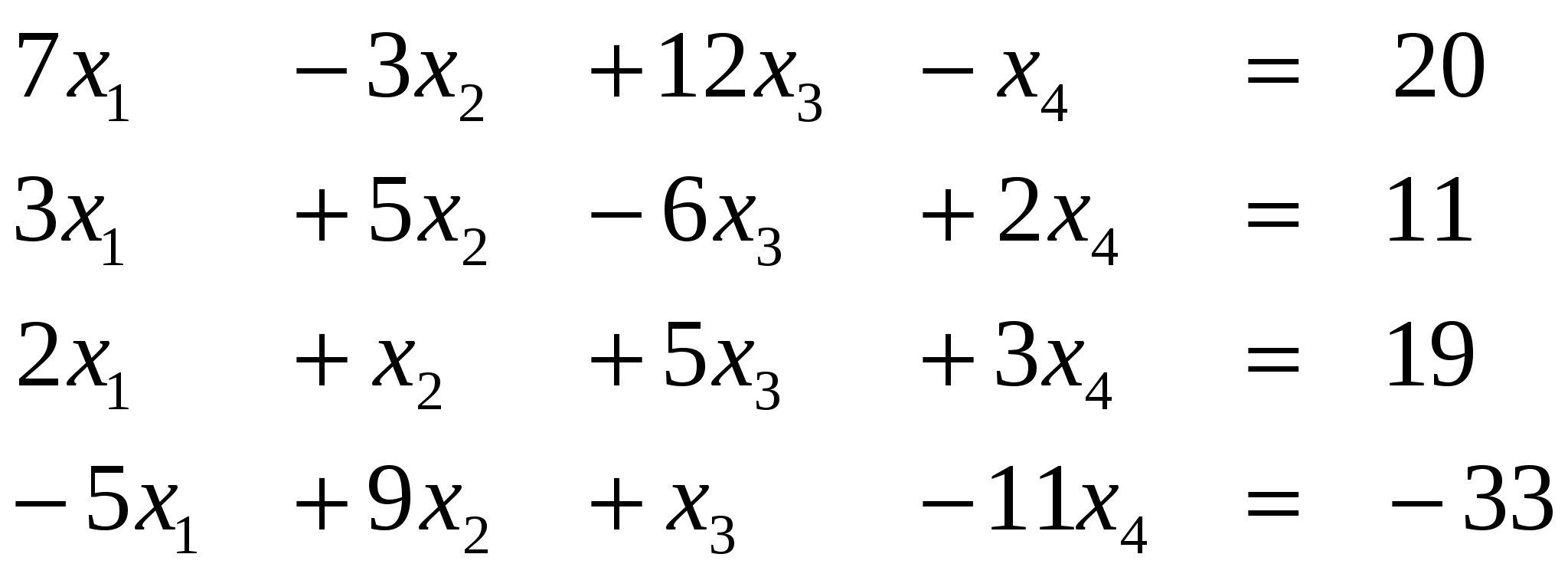 Ответ (2; ….) Ответ (2; ….)
|
Вариант 8
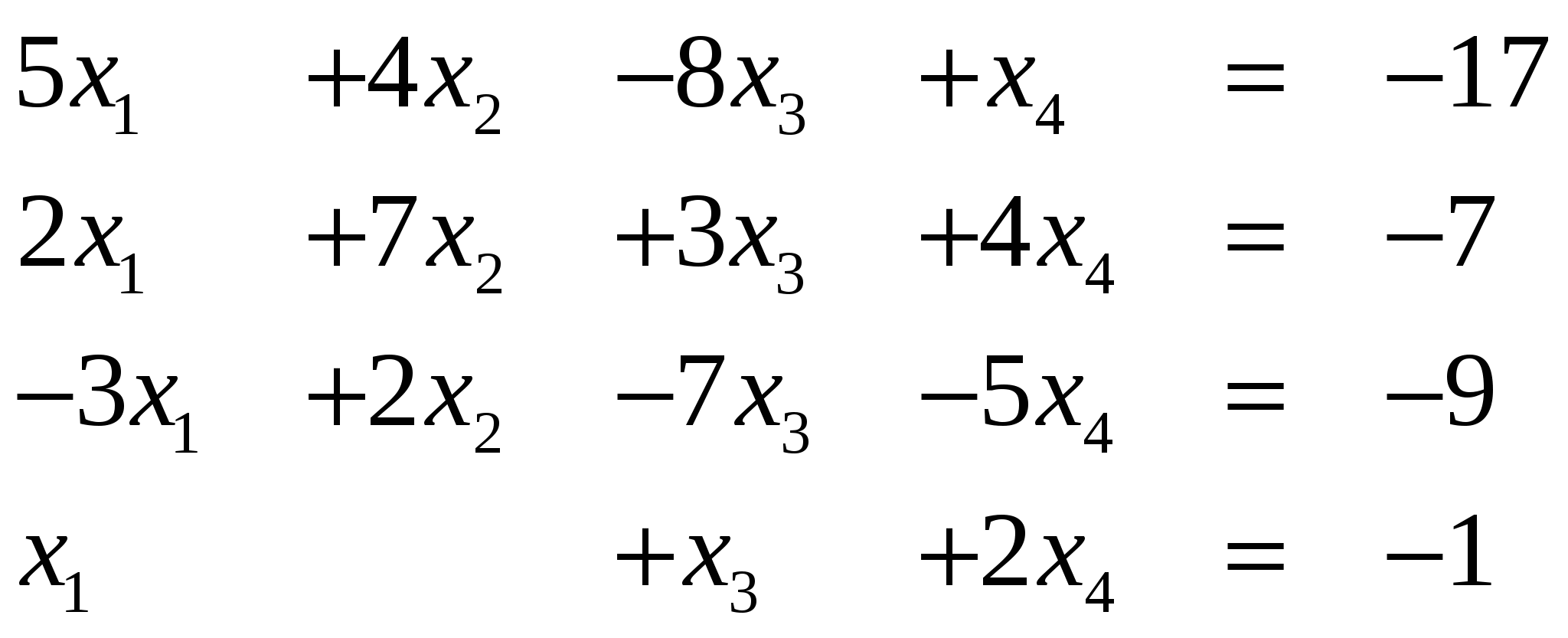 Ответ (1; ….) Ответ (1; ….)
|
Вариант 9
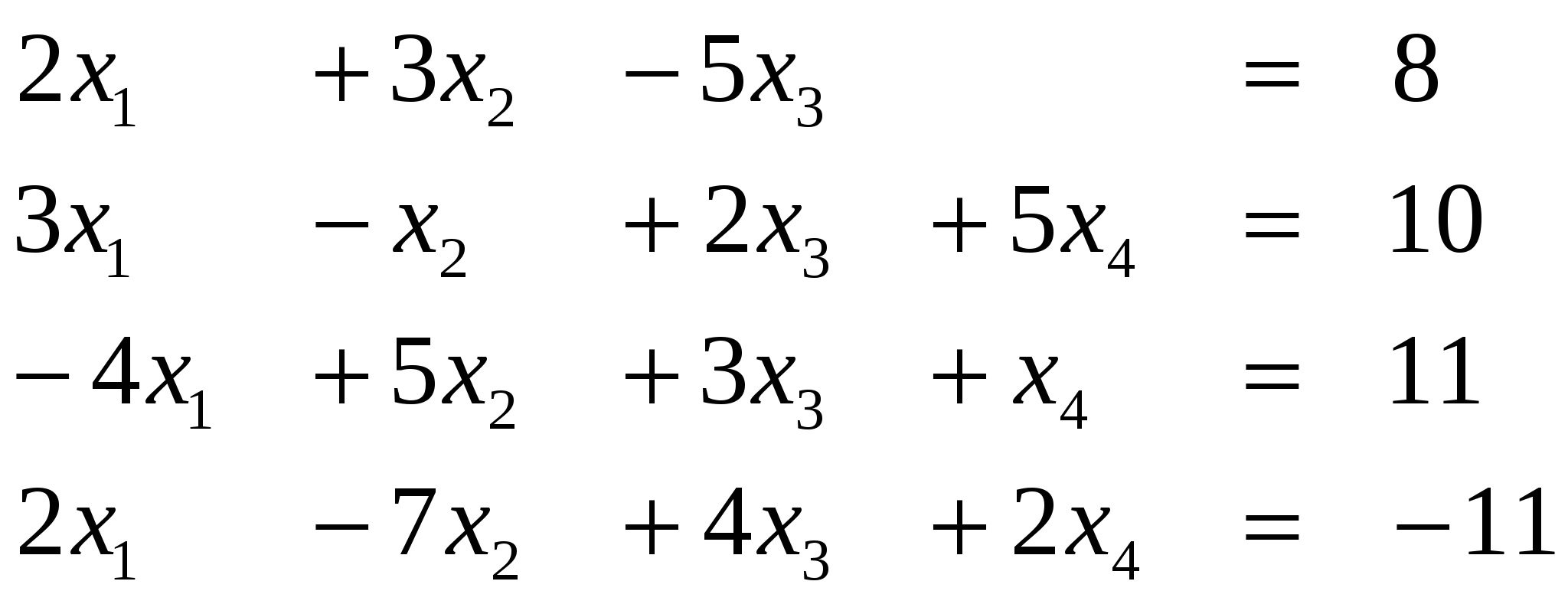
Ответ (2; ….)
|
Вариант 10
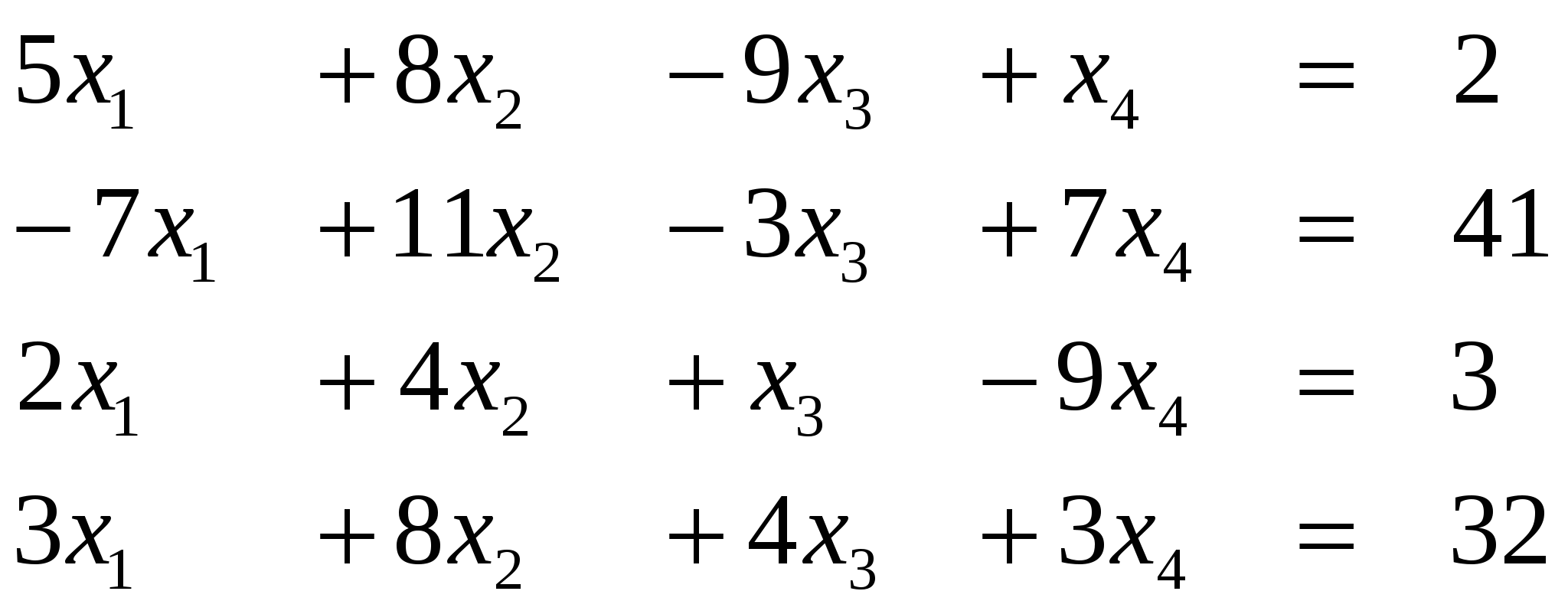
Ответ (-1; ….)
|
Вариант 11
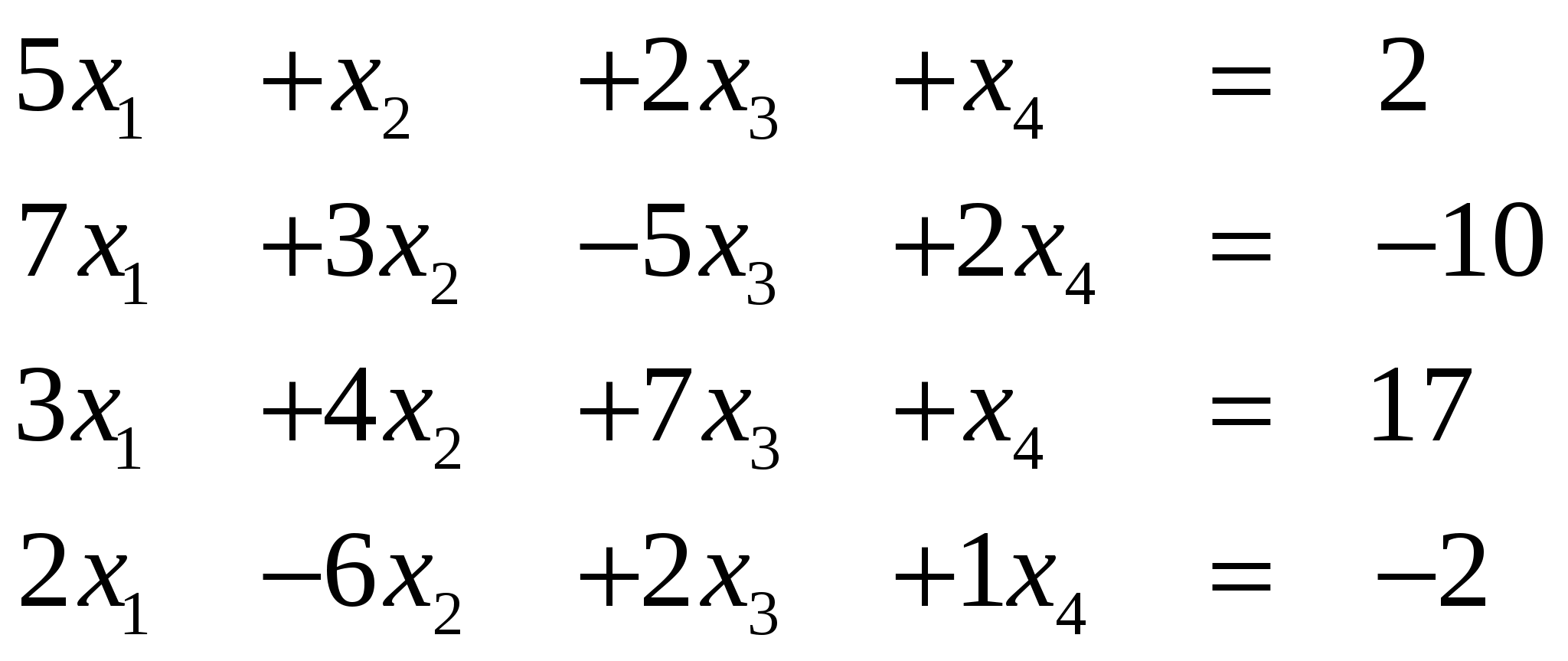
Ответ (-1; ….)
|
Вариант 12
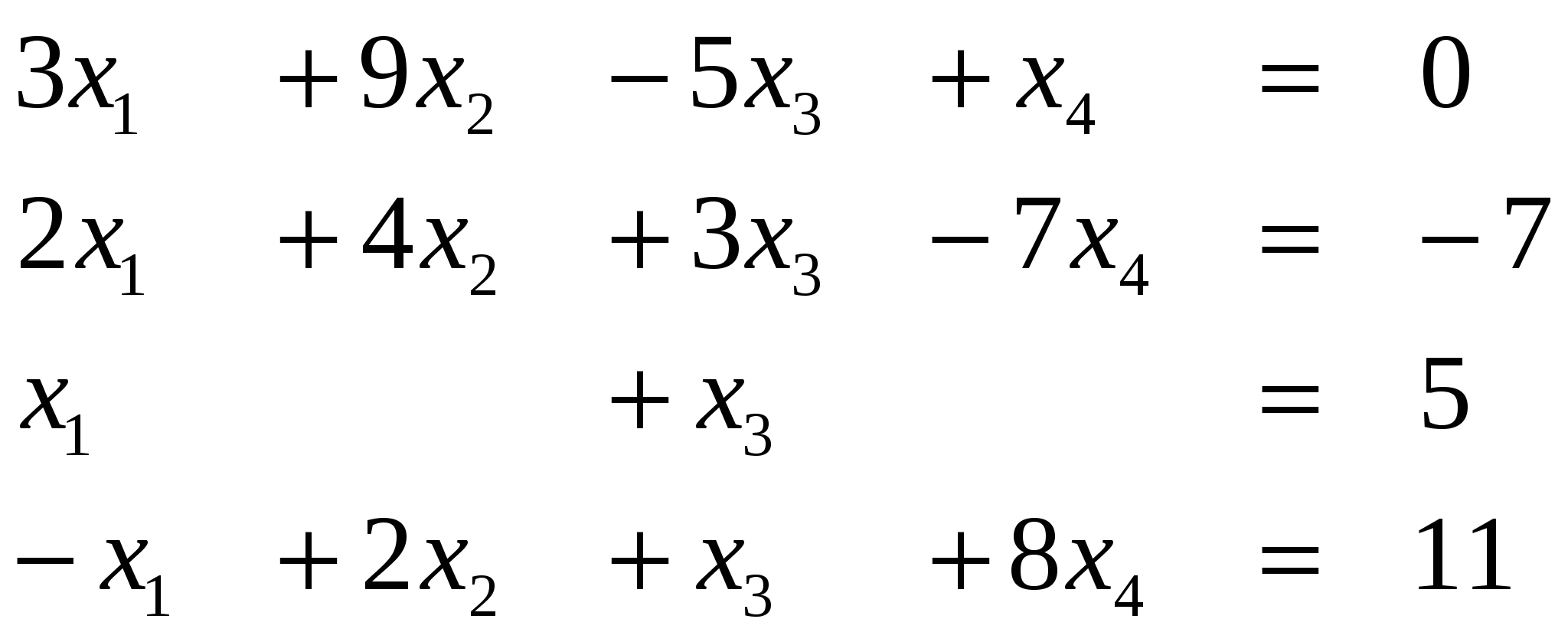
Ответ (4; ….)
|
Вариант 13
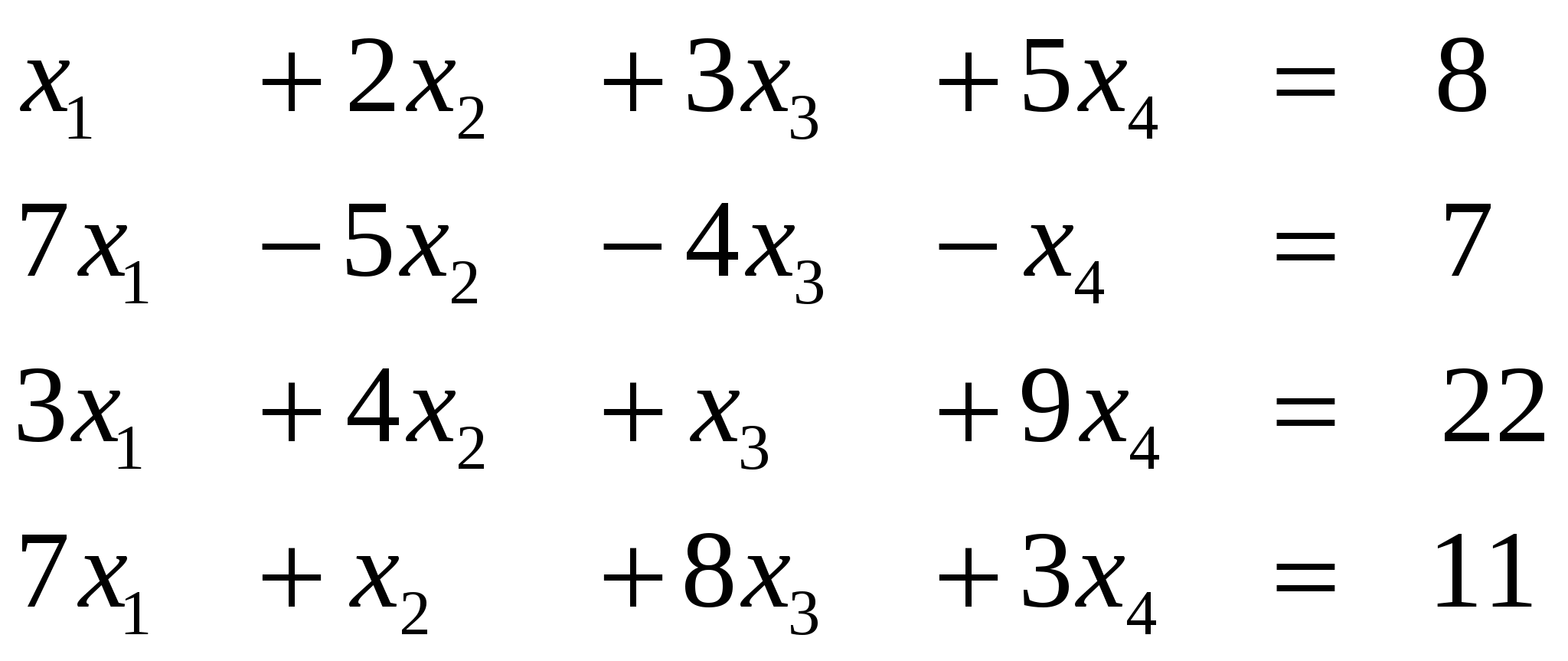
Ответ (2; ….)
|
Вариант 14
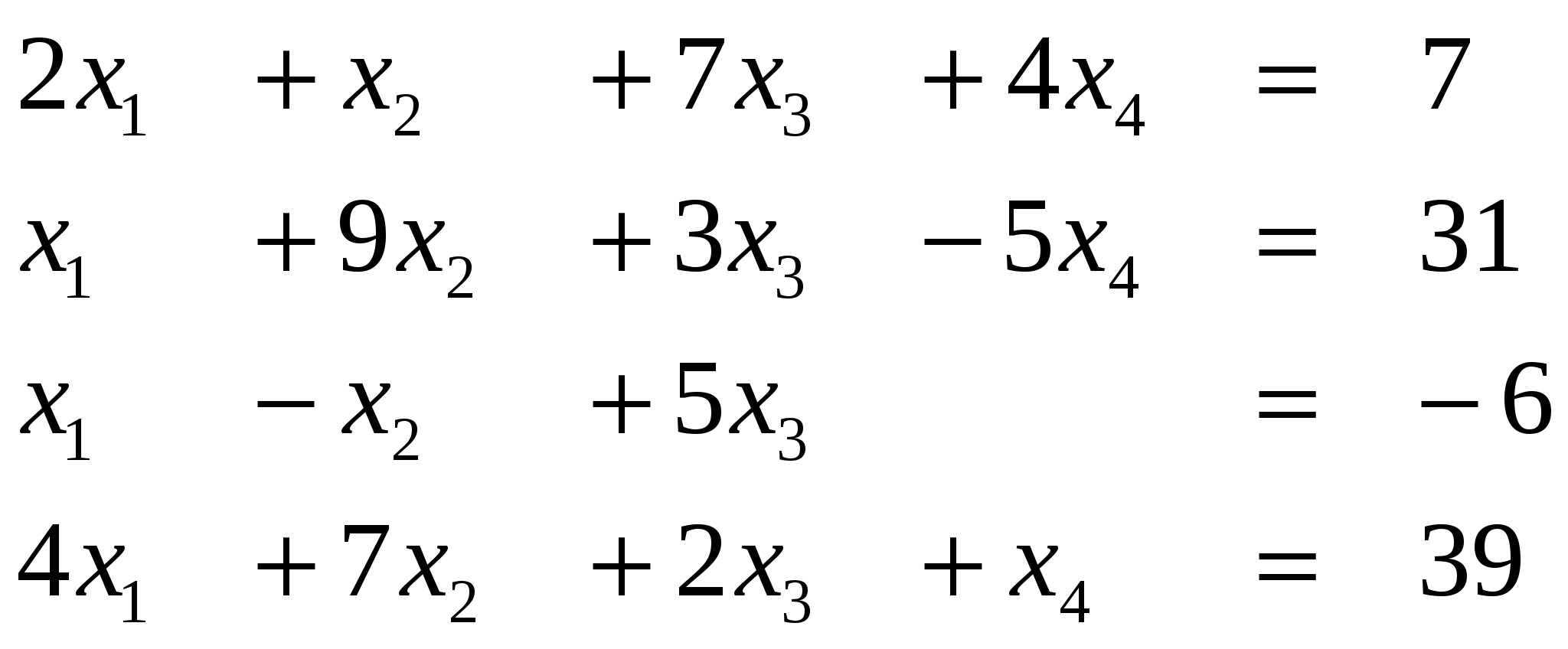
Ответ (3; ….)
|
Вариант 15
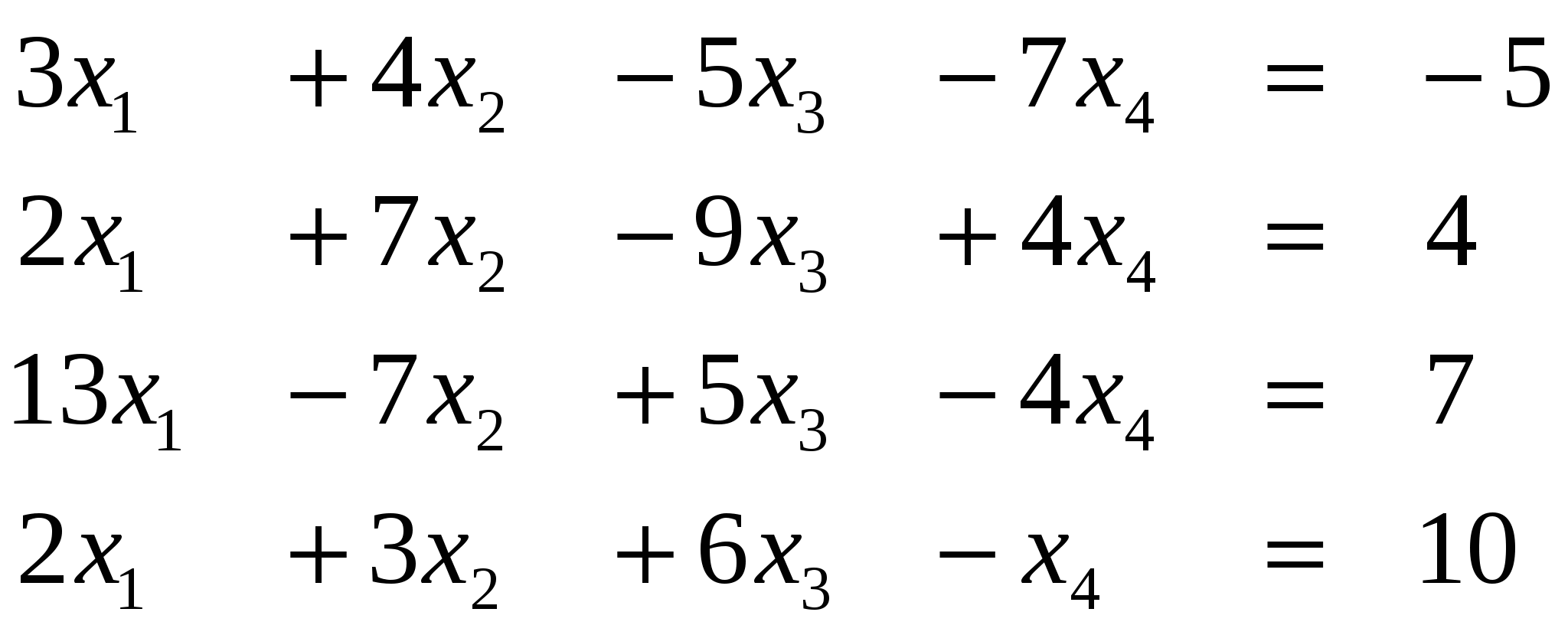
Ответ (1; ….)
|
Вариант 16
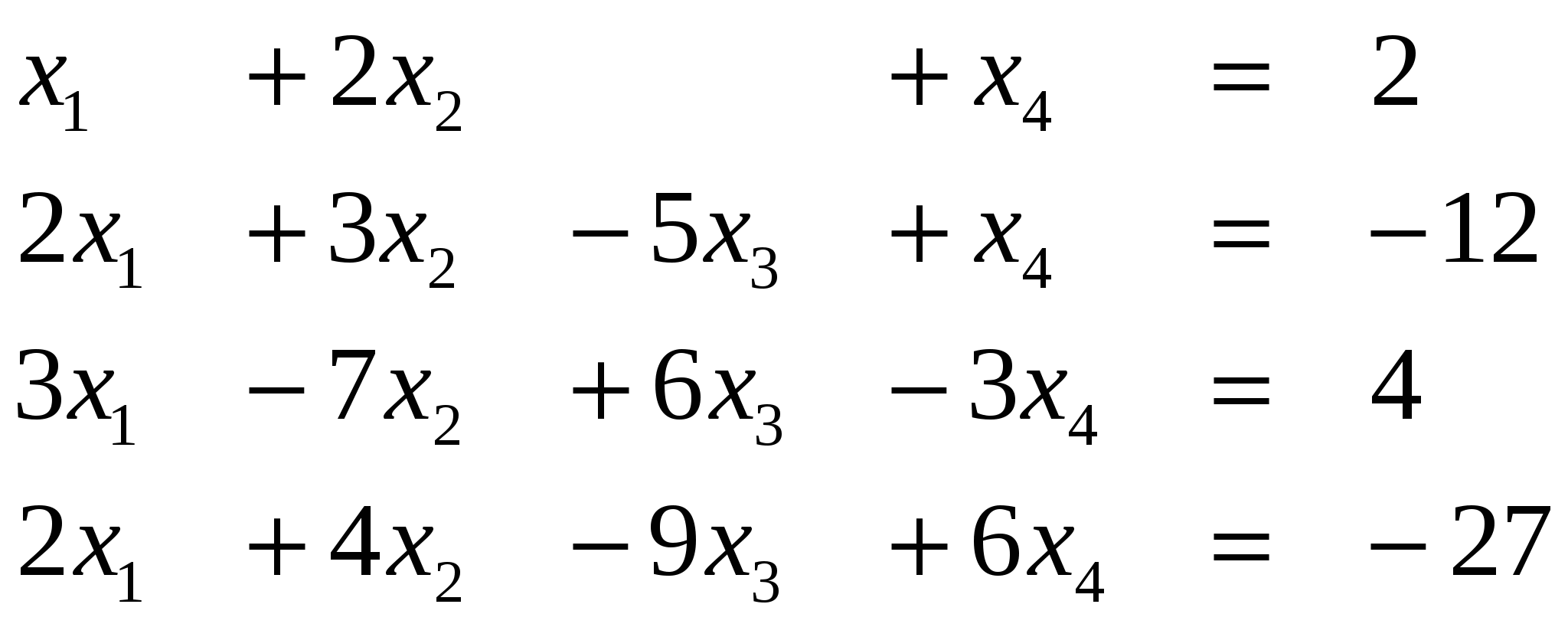
Ответ (-1; ….)
|
Вариант 17/
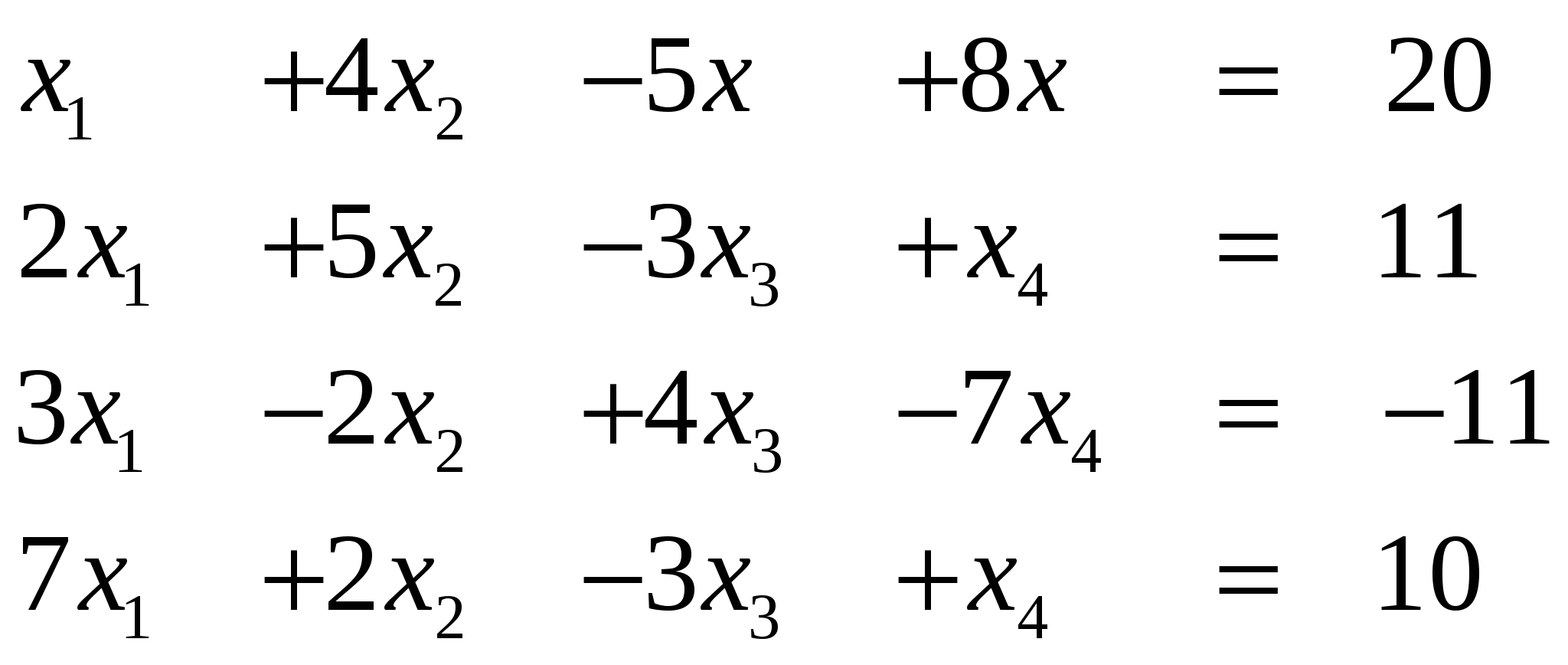
Ответ (1; …)
|
Вариант 18/
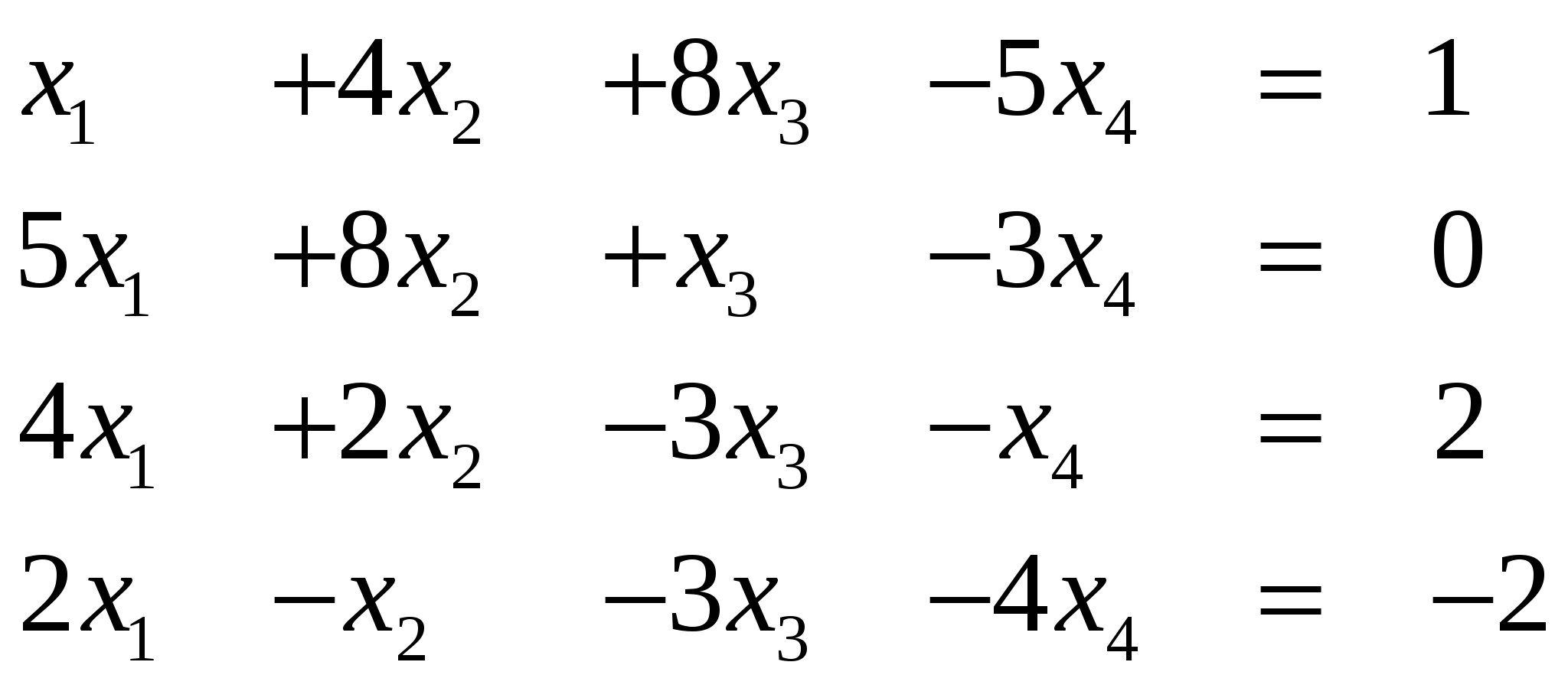
Ответ (2; …)
|
Вариант 19/
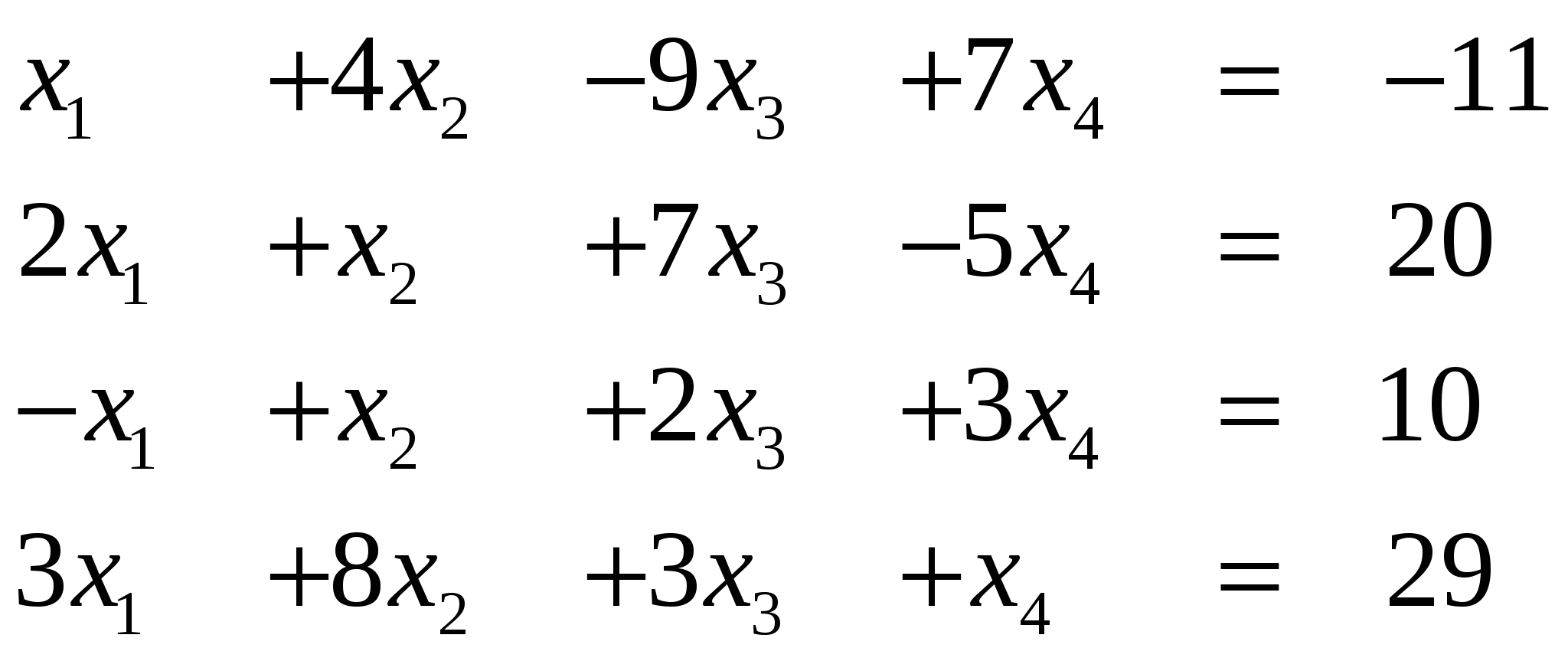
Ответ (1; …)
|
Вариант 20/
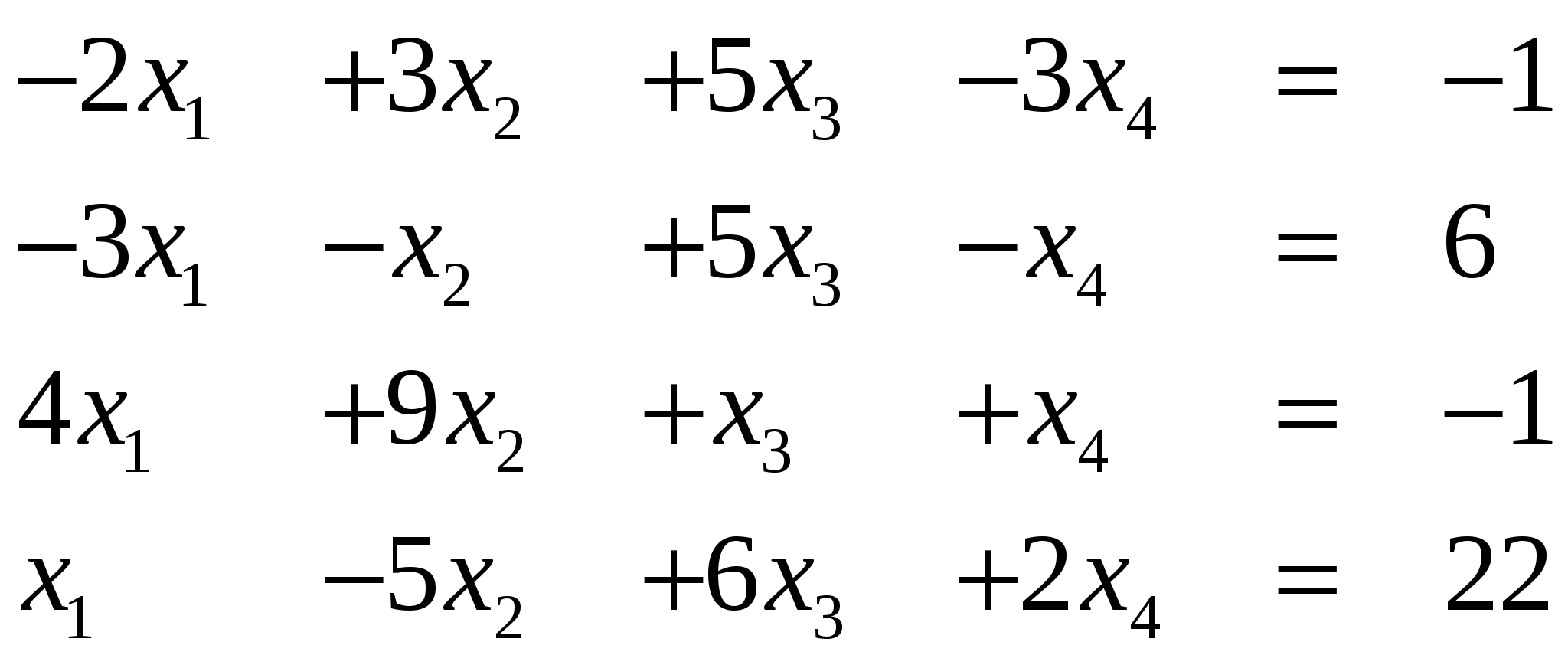
Ответ (1; …)
|
Вариант 21/
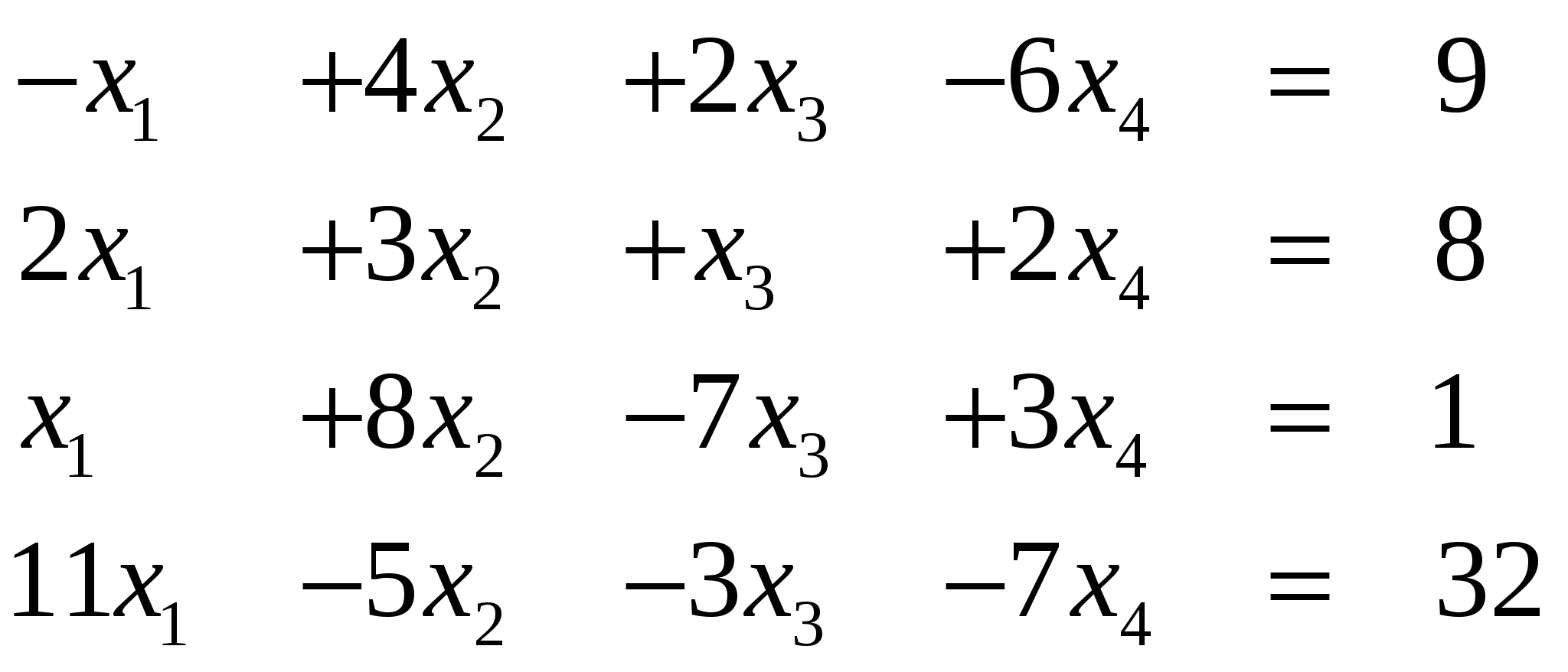
Ответ (3; ….)
|
Вариант 22/
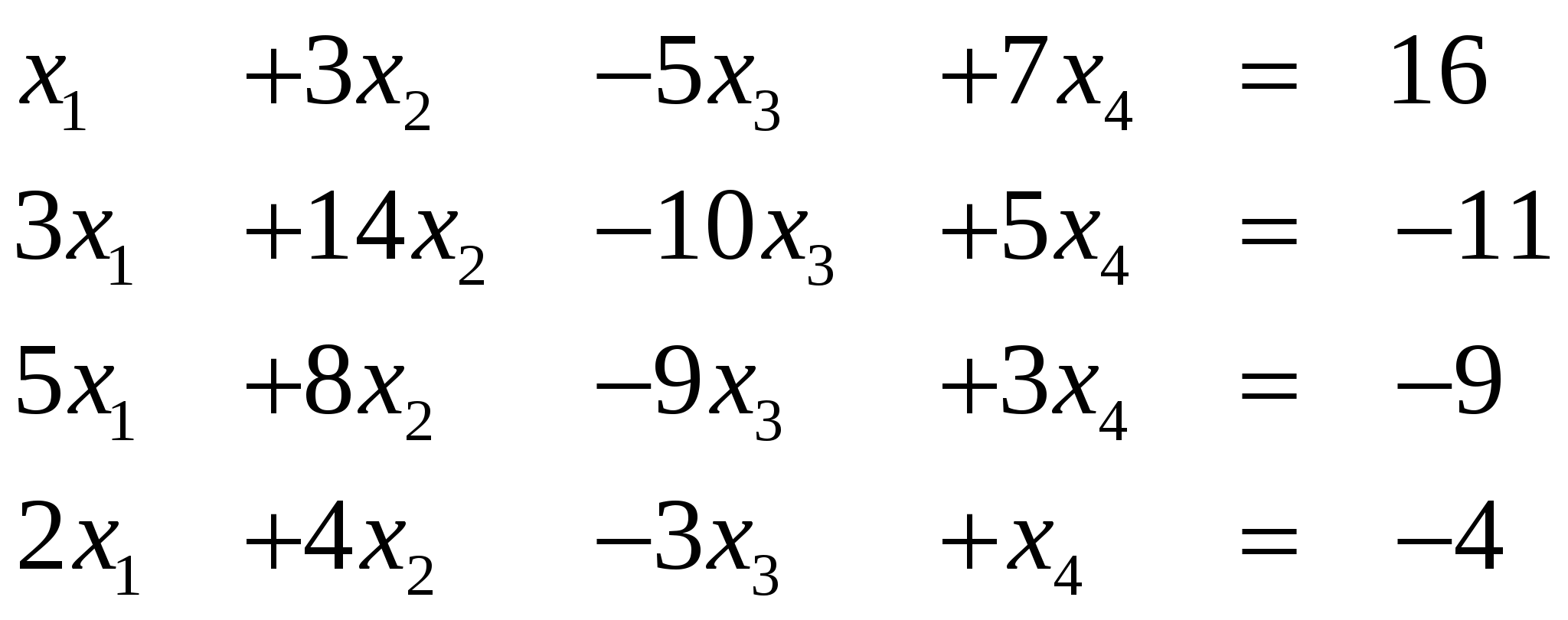 Ответ (1; ….) Ответ (1; ….)
|
Вариант 23/
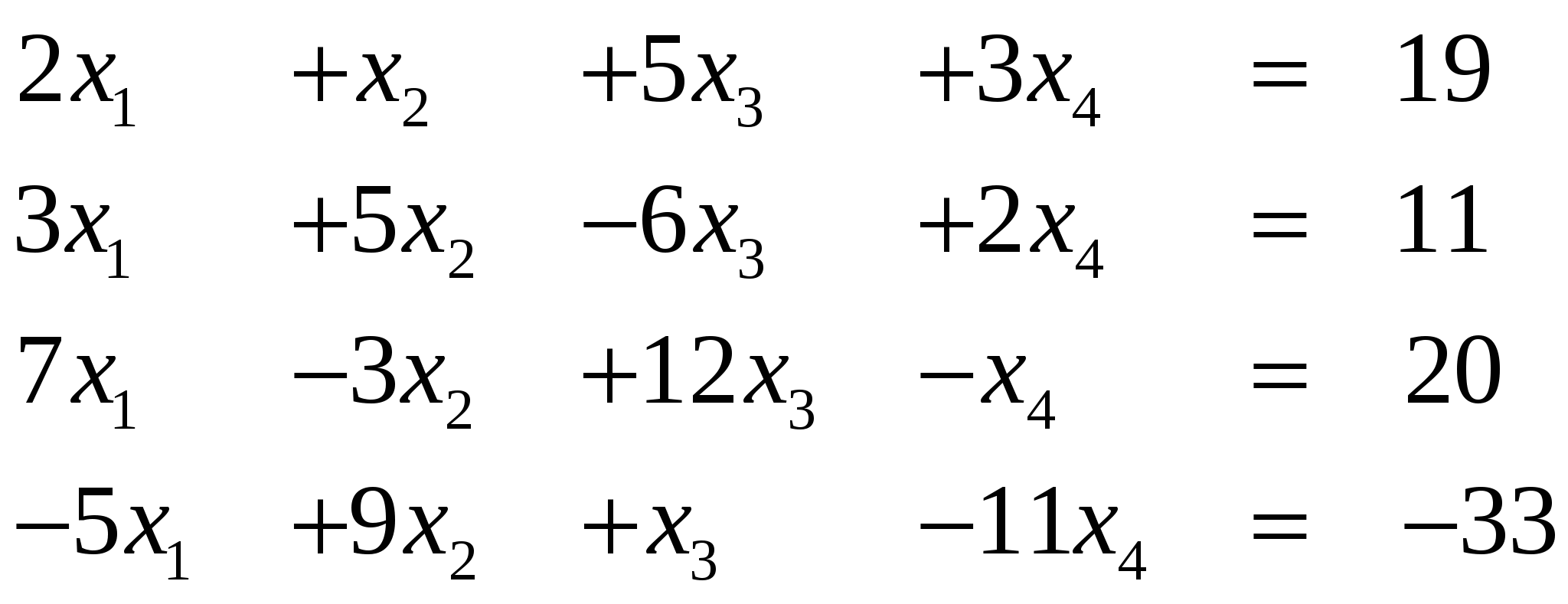 Ответ (2; ….) Ответ (2; ….)
|
Вариант 24/
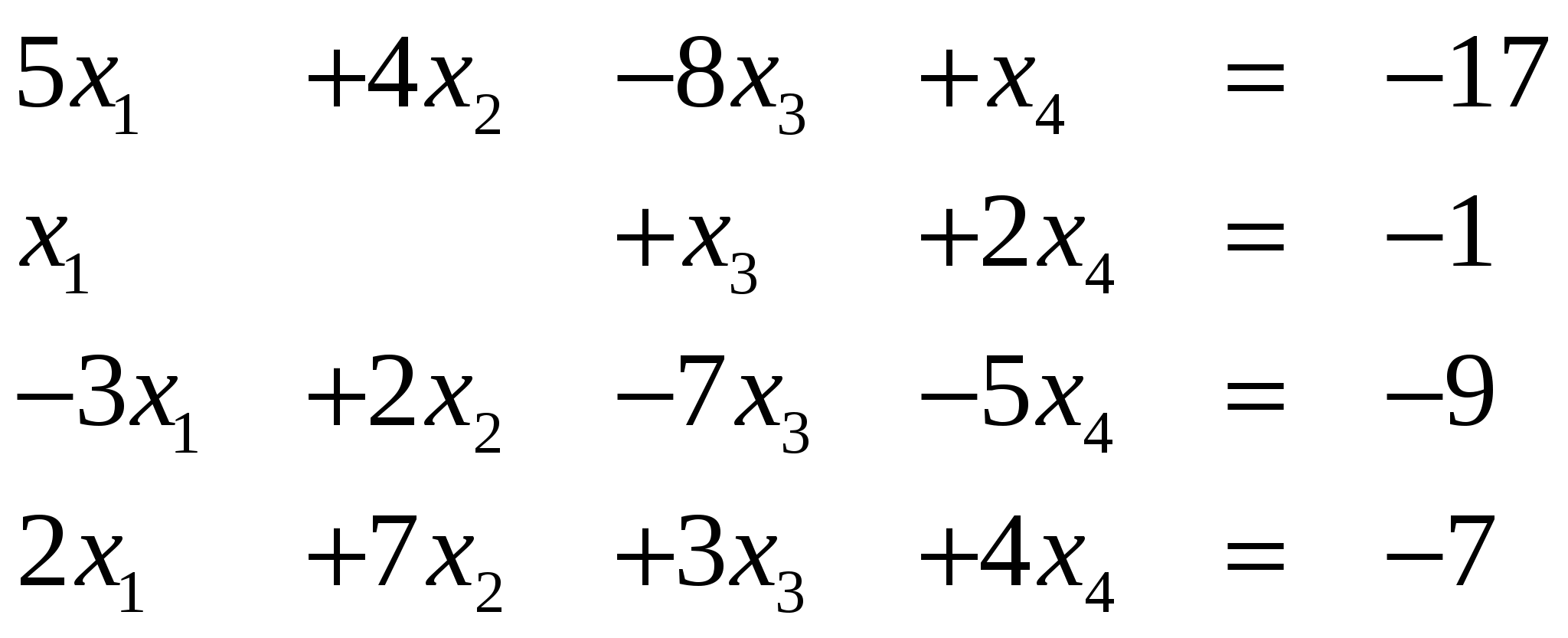 Ответ (1; ….) Ответ (1; ….)
|
Задание 2. Решить СЛАУ из задания 1 методом простой итерации и методом Зейделя, предварительно приведя ее к специальному виду, то есть к нормализованной форме: x=Bx+d. Сравнить их скорость сходимости.
Замечание: Если в Вашем варианте для нормализованной формы норма матрицы системы больше единицы, то метод простой итерации и метод Зейделя, соответственно, не сходятся.
В этом случае для реализации задания 2 в Вашем варианте предусмотрена дополнительная СЛАУ, смотрите ниже, с симметричной матрицей определённого вида. Поэтому эту СЛАУ, Ax = b, не нужно умножать на транспонированную матрицу Aт, чтобы перейти к СЛАУ с симметричной матрицей, а применить нормализованную форму СЛАУ, x = Bx + d, с матрицей B = I – L-1A, где d = L-1b и L-1 – диагональная матрица. В ней только диагональные элементы (L-1)ii = 1/Aii 0. Необходимо убедиться, что норма матрицы B меньше единицы, ||B|| < 1, и решить эту СЛАУ итерационными методами. Точность решения ||x* – xn|| 10–4, вектор xn получен в n-ой итерации.
СЛАУ дополнительного варианта:
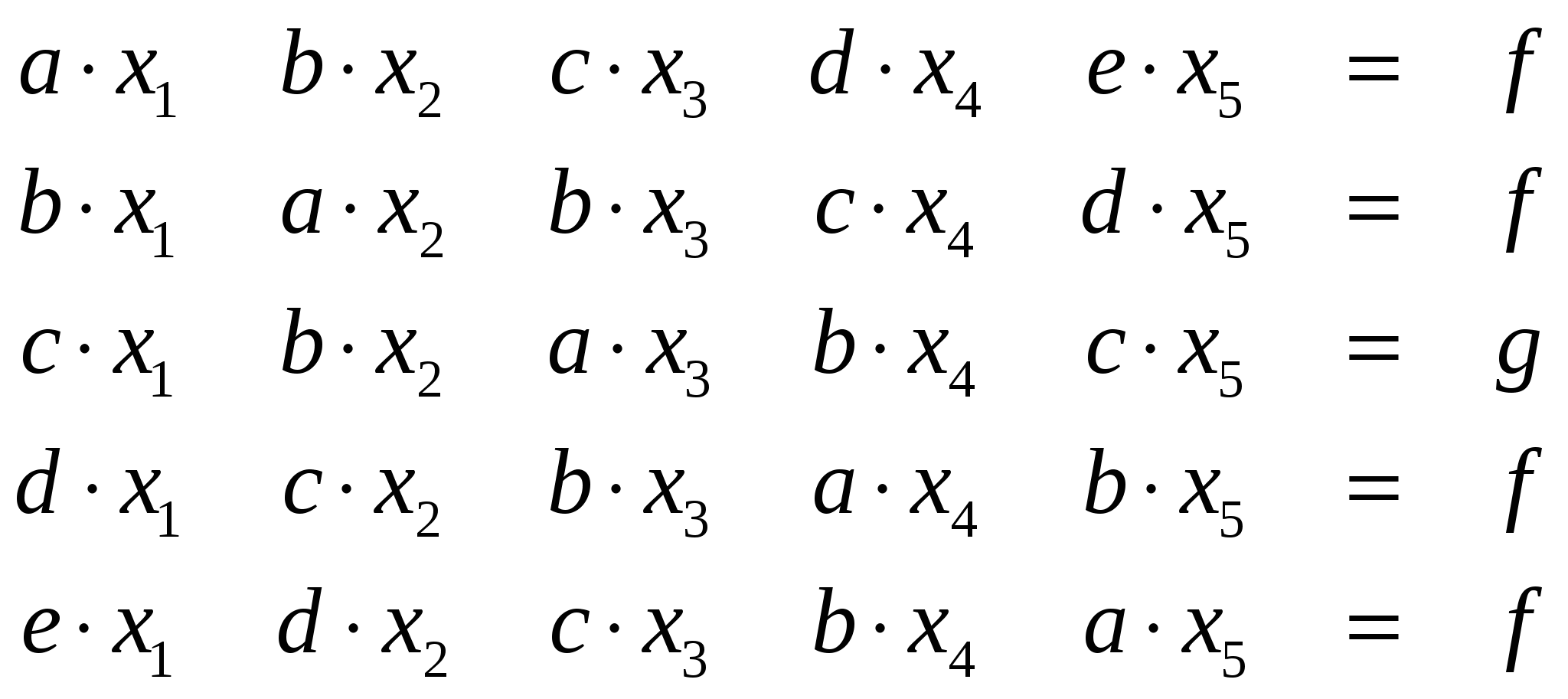 ; ;
Варианты значений для величин, обозначенных латинскими буквами:
Вариант
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
№1-№5
|
n+5
|
0
|
-2
|
0
|
1
|
1
|
n+5
|
№6-№10
|
n+5
|
2
|
1
|
0
|
0
|
2
|
n+5
|
№11-№15
|
n
|
4
|
0
|
0
|
2
|
3
|
n
|
№16-№20
|
n+5
|
6
|
2
|
1
|
1
|
4
|
n+5
|
№21-№25
|
n+5
|
8
|
4
|
2
|
2
|
5
|
n+5
|
№26-№30
|
n+5
|
10
|
8
|
3
|
0
|
5
|
n+5
|
Вопросы к защите лабораторной работы №3
«Решение систем линейных алгебраических уравнений»
Метод Гаусса и метод Жордана-Гаусса (схема единственного деления): описание методов, их трудоемкость.
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора): описание метода, его вычислительная устойчивость.
Метод простой итерации (Якоби) для решения систем линейных алгебраических уравнений. Его геометрическая иллюстрация.
Алгоритмы приведения к виду, обеспечивающему сходимость итерационного процесса.
Метод Зейделя для решения систем линейных алгебраических уравнений. Его сходимость, оценки погрешности, критерий окончания итераций.
ЛАБОРАТОРНАЯ РАБОТА №4
Решение нелинейных уравнений
Задание для решения одного уравнения
Путём ручного просчета (с обязательным привлечением любого из математических пакетов для проведения вычислений и составления таблиц и графиков, включаемых в отчёт) найти корень заданного уравнения 2-мя методами (из 4-ёх изложенных в лекции) с заданной точностью. Отделение корней провести графически (или составлением таблицы значений функции, контролируя шаг изменения её аргумента, а интервал, где её график может пересечь ось ОХ, оценить из анализа поведения функции с помощью производных). В отчёт включить: уравнение, информацию, поясняющую способ отделения его корней графиком или таблицей, формулы, реализующие методы уточнения корней, промежуточные вычисления по ним. Результаты свести в итоговую таблицу:
№ итерации
|
Xn
|
F(Xn)
|
|Xn-Xn-1| или |Bn-An|
|
(Xn)= |Xn-Xn-1|/|Xn|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Для каждого уравнения необходимо найти хотя бы один корень. Если уравнение имеет более одного корня, отыскать корень ближайшие к началу координат.
Номер уравнения выбрать по формуле:
k+21(q-1).
Здесь k – номер студента в списке группы; q = 1 для группы А и 2 для группы Б.
Допустимая погрешность вычисляется по формуле:
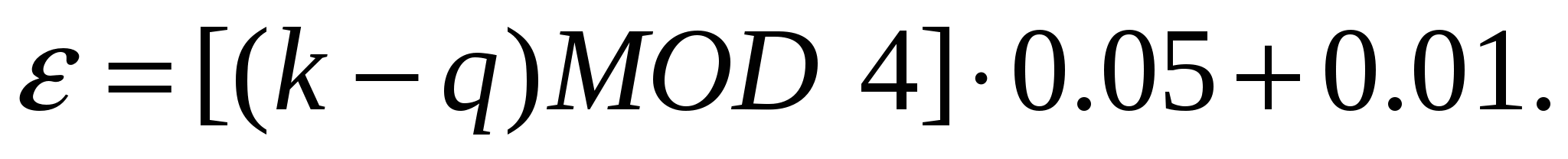
Студенты, номер которых в списке нечётный, решают систему методами дихотомии и простой итерации, а студенты с чётным номером – методами хорд и касательных.
Варианты к заданию
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .
 . .





Задание для решения системы 2-х уравненийСоставить программу для ЭВМ, находящую решения системы 2-х уравнений с двумя неизвестными (согласно варианту задания) методами простой итерации и Ньютона с произвольно заданной точностью. (Замечание: можно использовать любой язык программирования или прикладной математический пакет.) Требования к программеРеализация программы на языке программирования высокого уровня имеет
Вывод учетной информации о программе, (тема, Ф.И.О. автора).
Наличие меню для выбора метода поиска решения с указанием вида соответствующих систем.
Для выбора начального приближения графическим методом в программе должна быть предусмотрена возможность вывода на экран графика каждой из функций. При невозможности явно выразить одну из переменных из уравнений (2.1) для построения графиков следует воспользоваться методом построчного сканирования, как в программе GFxy.
Ввод после выбора метода решения значений x иy начального приближения и величины допустимой погрешности.
Программа должна быть в состоянии найти все корни данного уравнения указанным методом, если их конечное число, или три ближайших к началу координат корня, если уравнение имеет бесконечное число корней.
Вывести результаты расчета на экран в виде таблицы:
№ итерации
|
xn
|
yn
|
|xn-xn-1|
|
|yn-yn-1|
|
F(x)
|
G(x)
|
|
|
|
|
|
|
| Замечание. Графики функций можно строить, используя пакеты прикладных программ ( Excel, MathCAD, MatLab и т. п.). Допустимо применение таких математических пакетов и для пошаговой, циклами, реализации всего алгоритма поиска решения системы нелинейных уравнений. Требования к отчетуОтчет должен содержать следующие обязательные пункты:
титульный лист установленного образца;
формулировку задания;
краткие теоретические сведения о применяемых методах;
графики функций;
результаты расчетов: и ручного, и при помощи программы;
текст программы;
выводы.
Варианты к заданию






















|
|
|
 Скачать 473.5 Kb.
Скачать 473.5 Kb.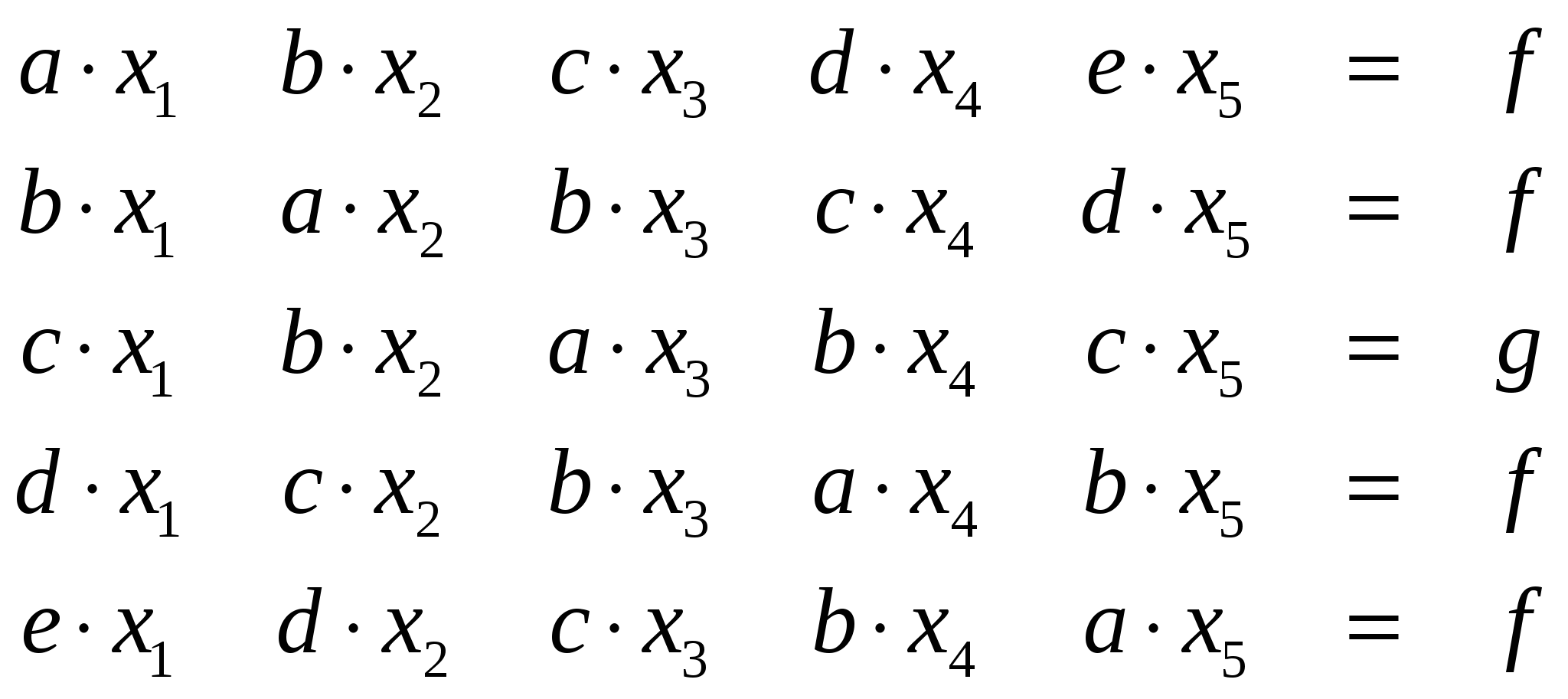 ;
; 
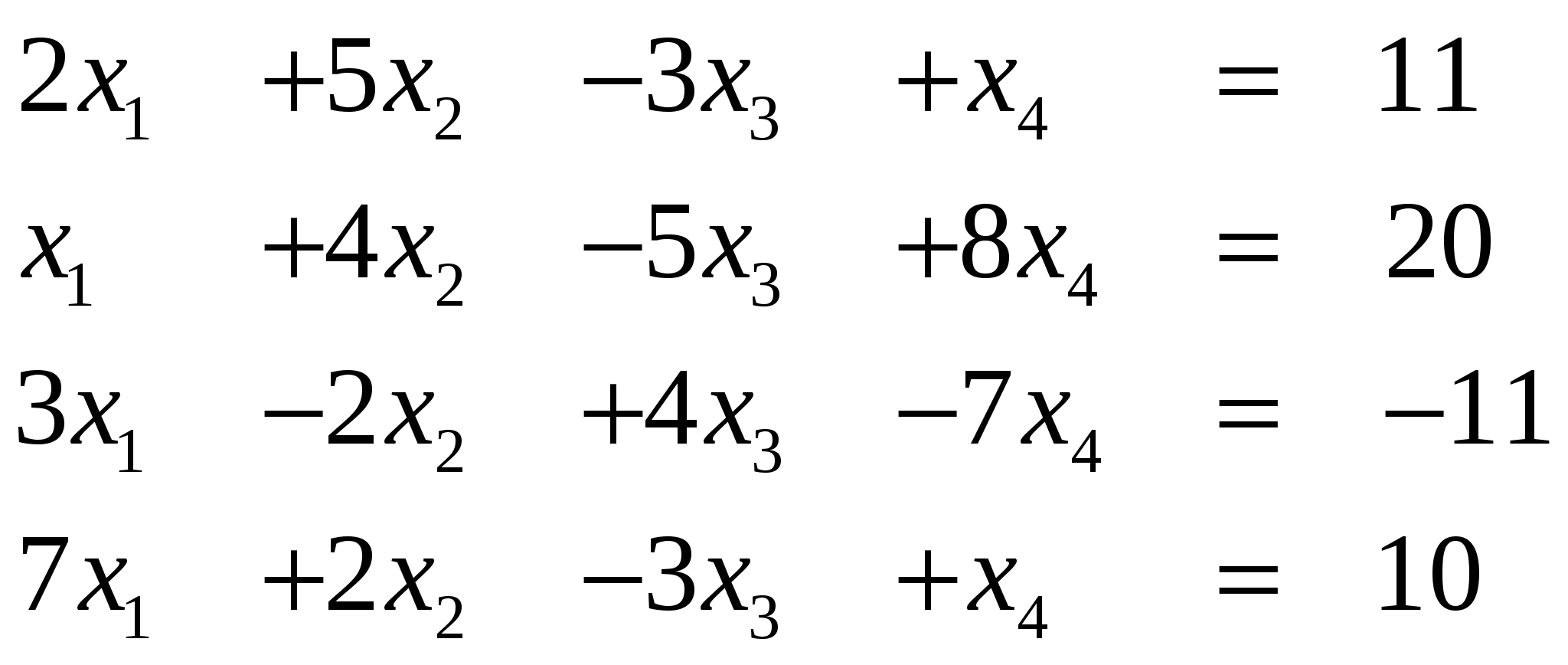
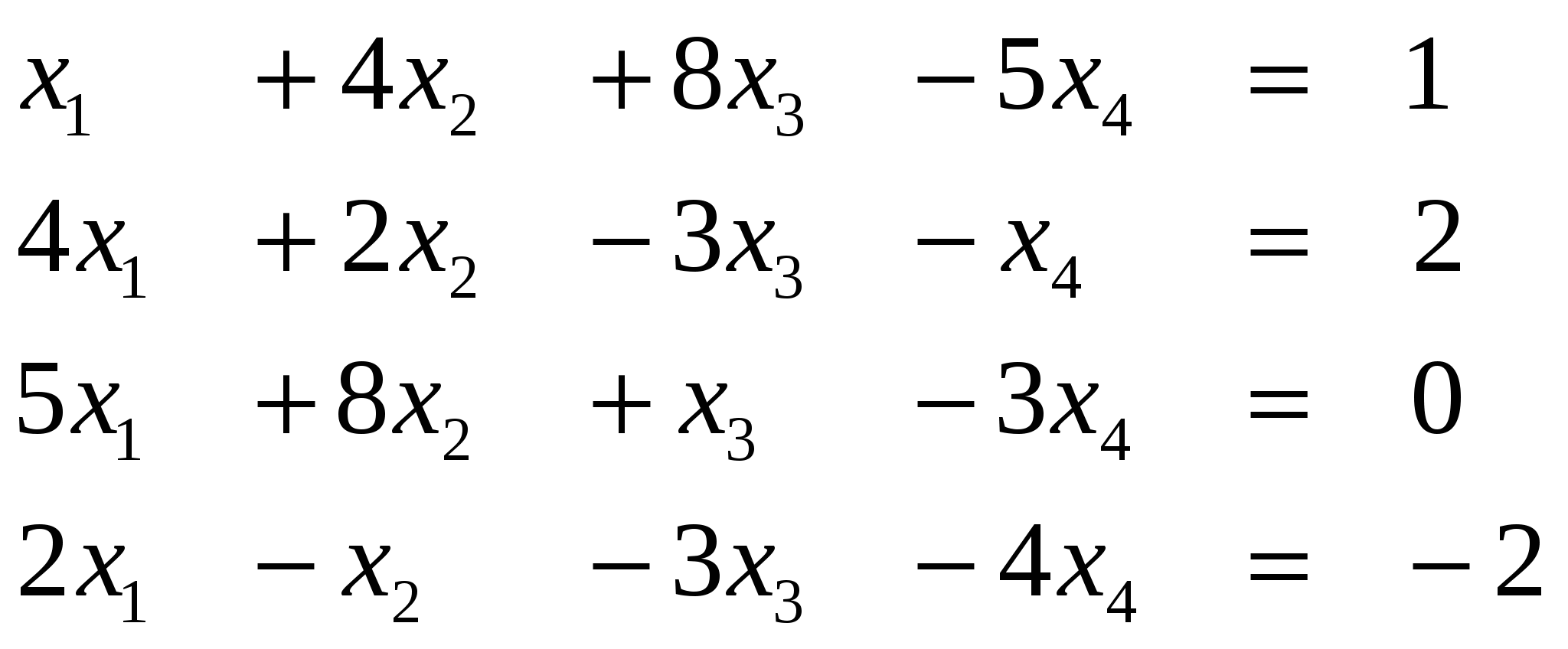
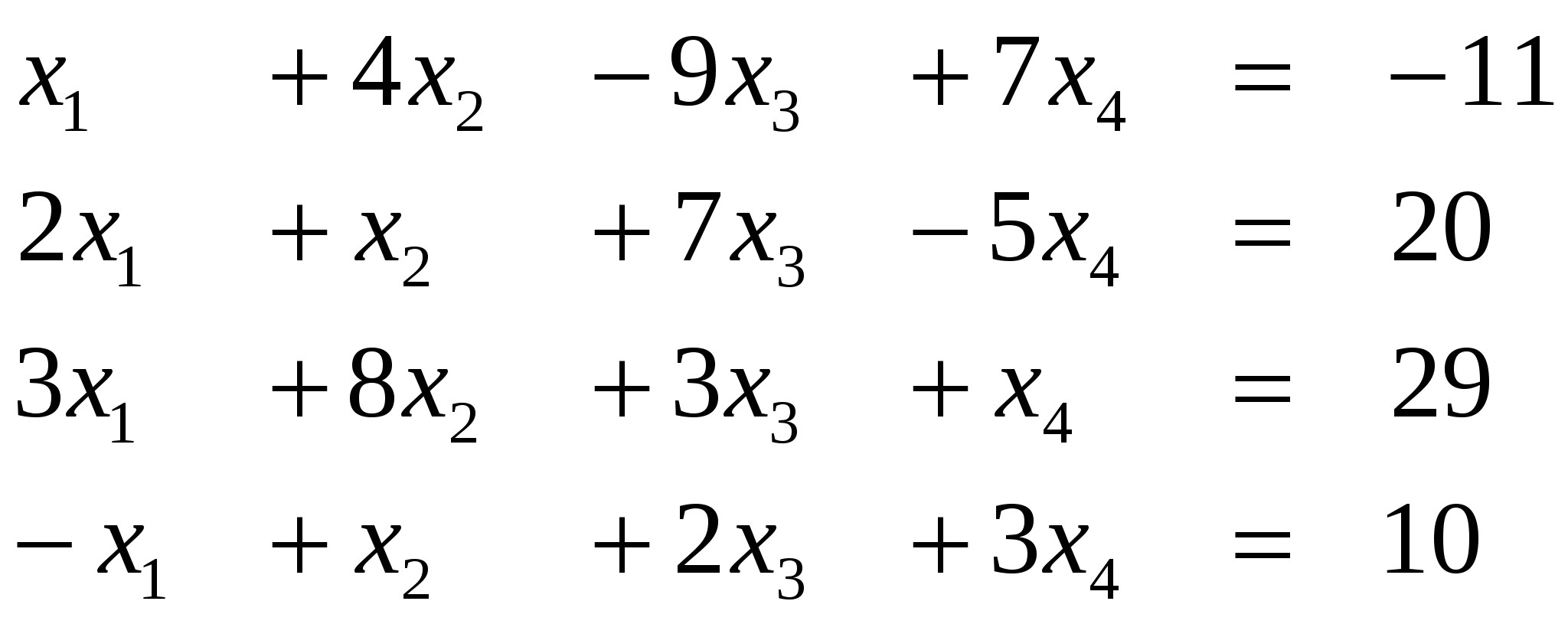
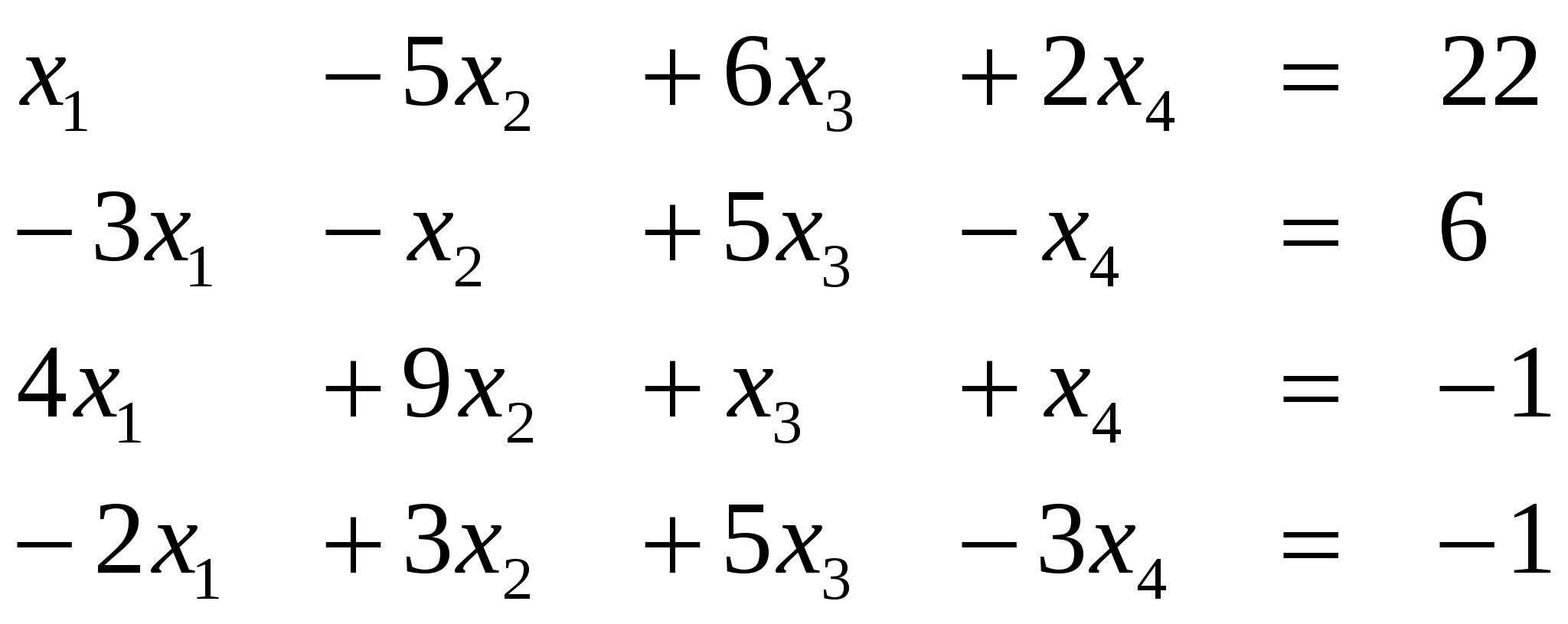
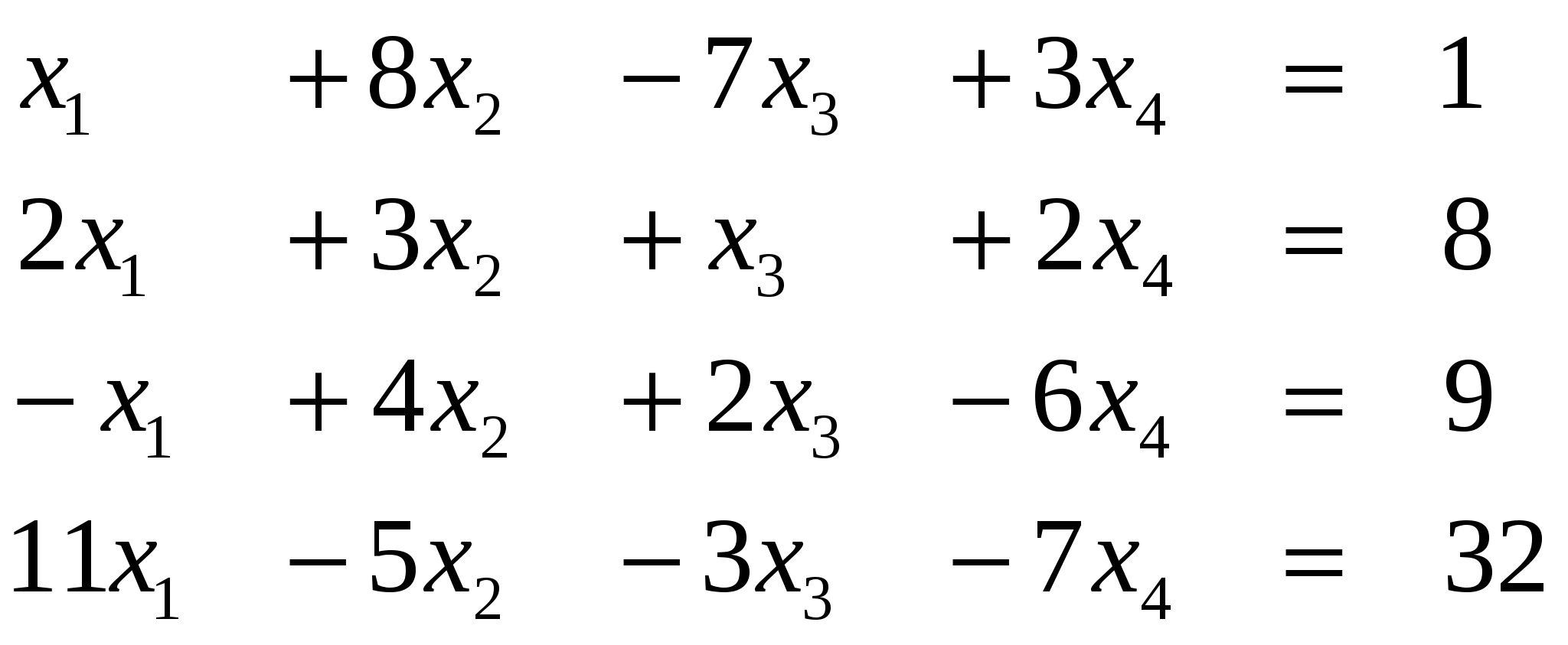
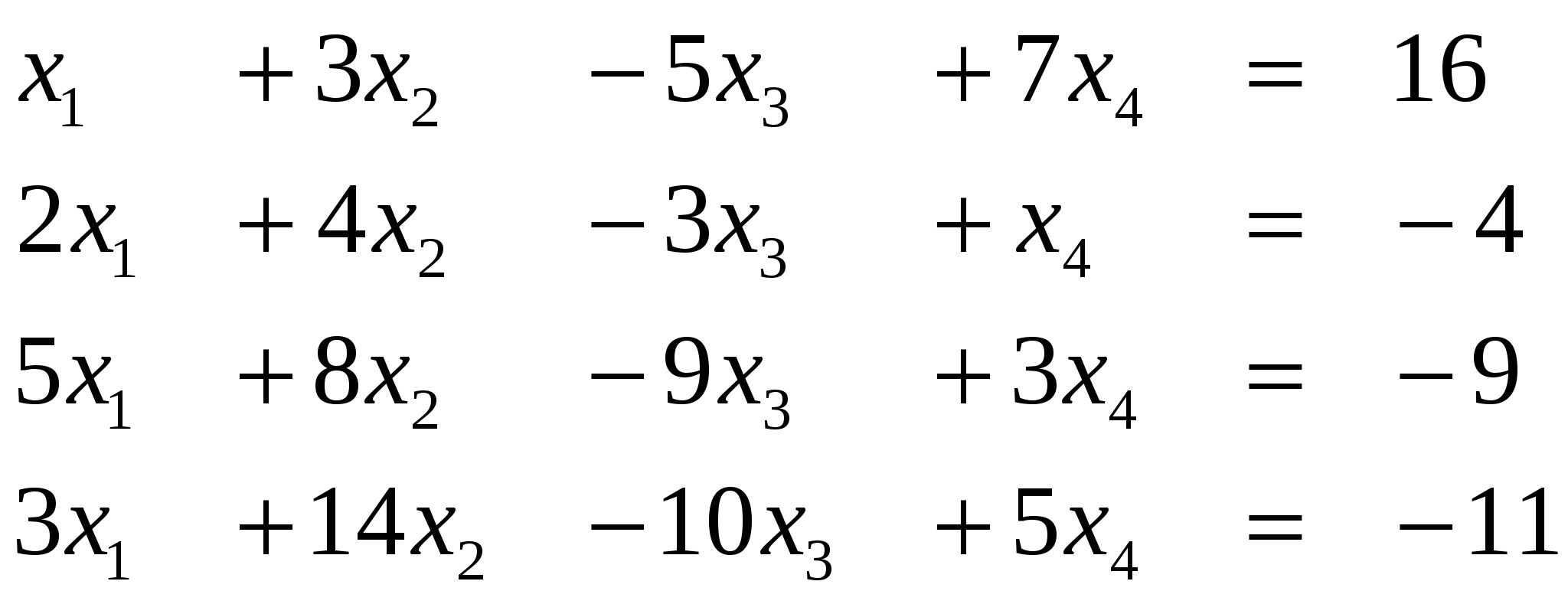 Ответ (1; ….)
Ответ (1; ….)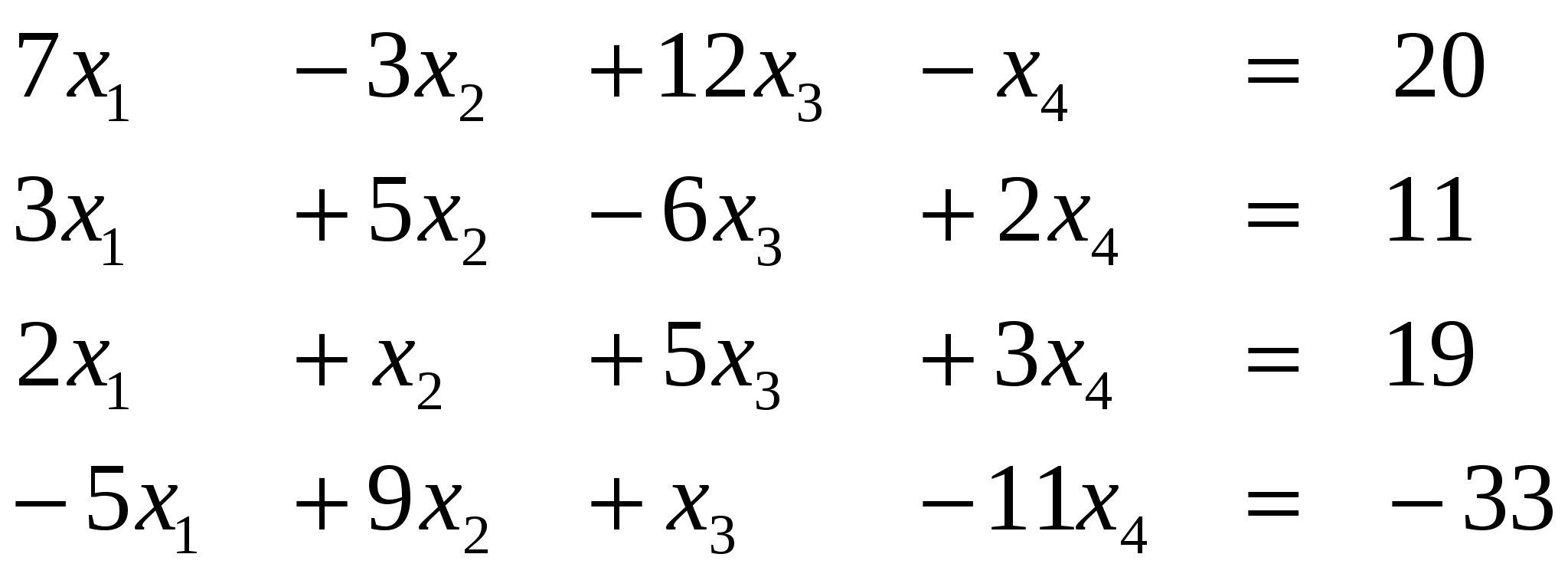 Ответ (2; ….)
Ответ (2; ….)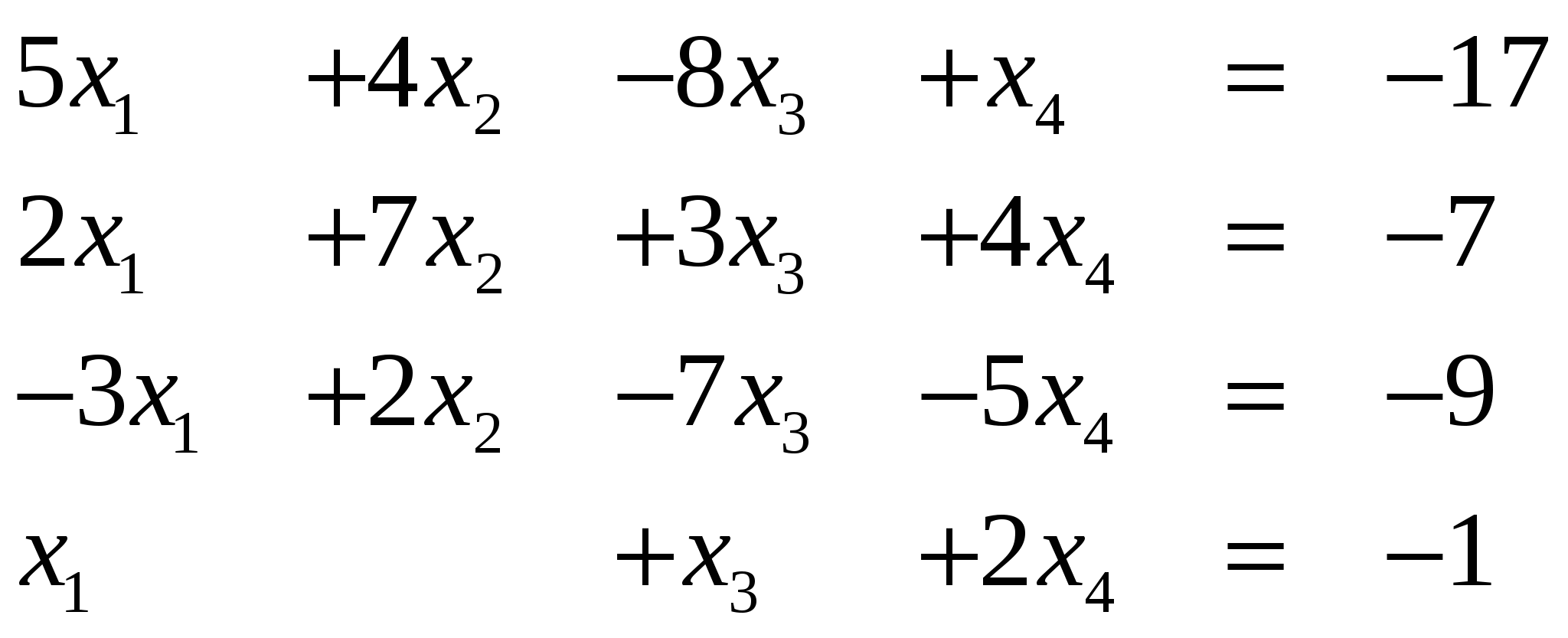 Ответ (1; ….)
Ответ (1; ….)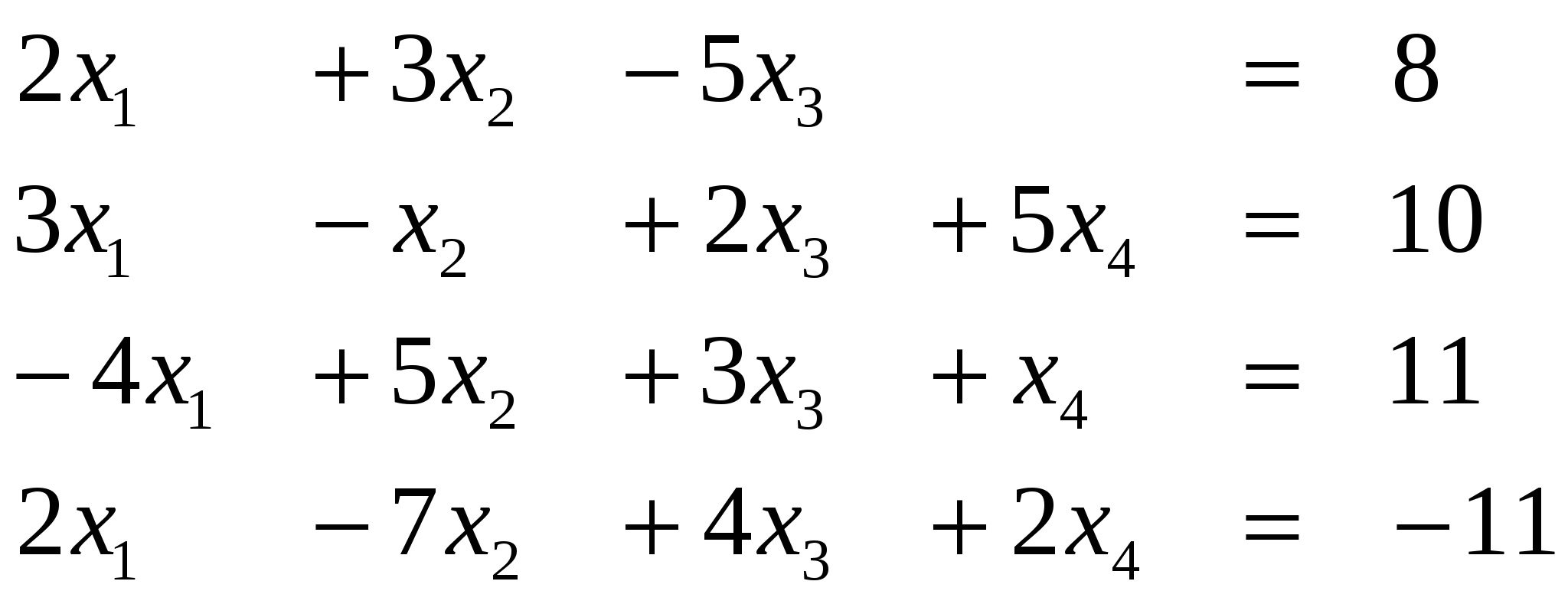
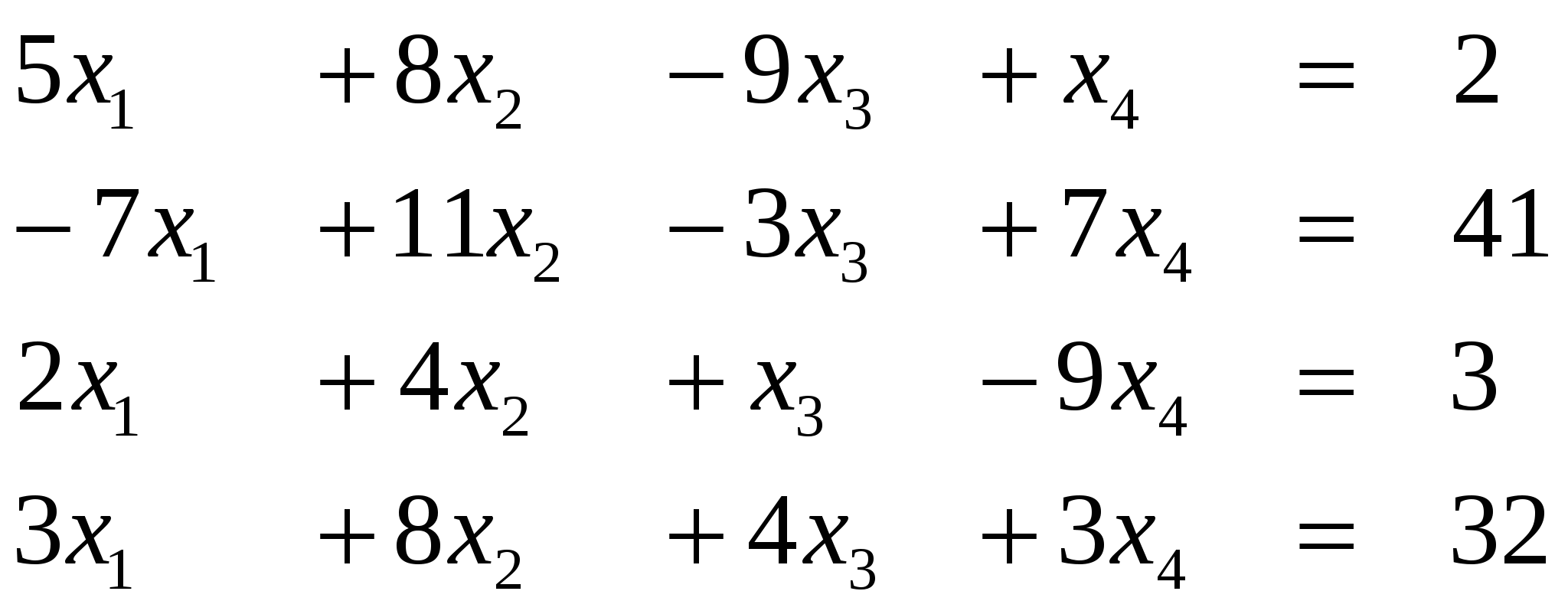
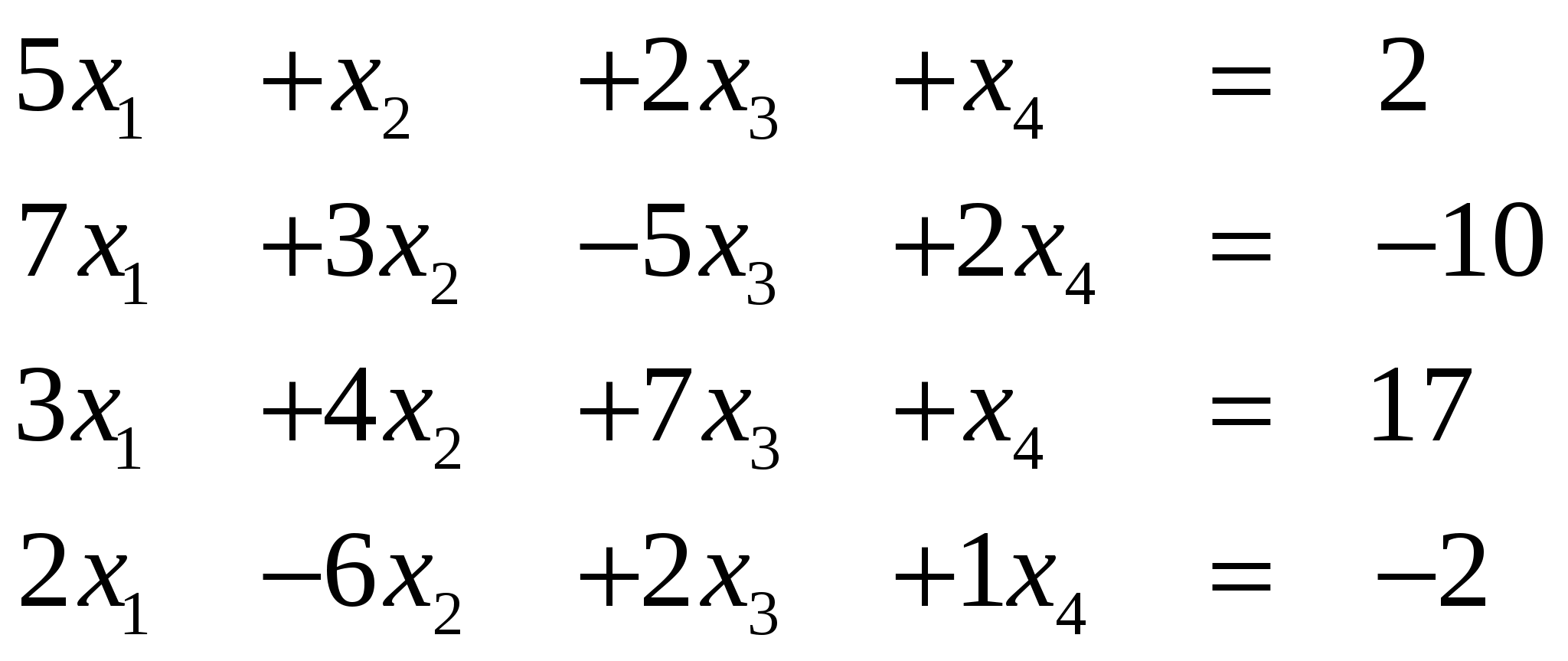
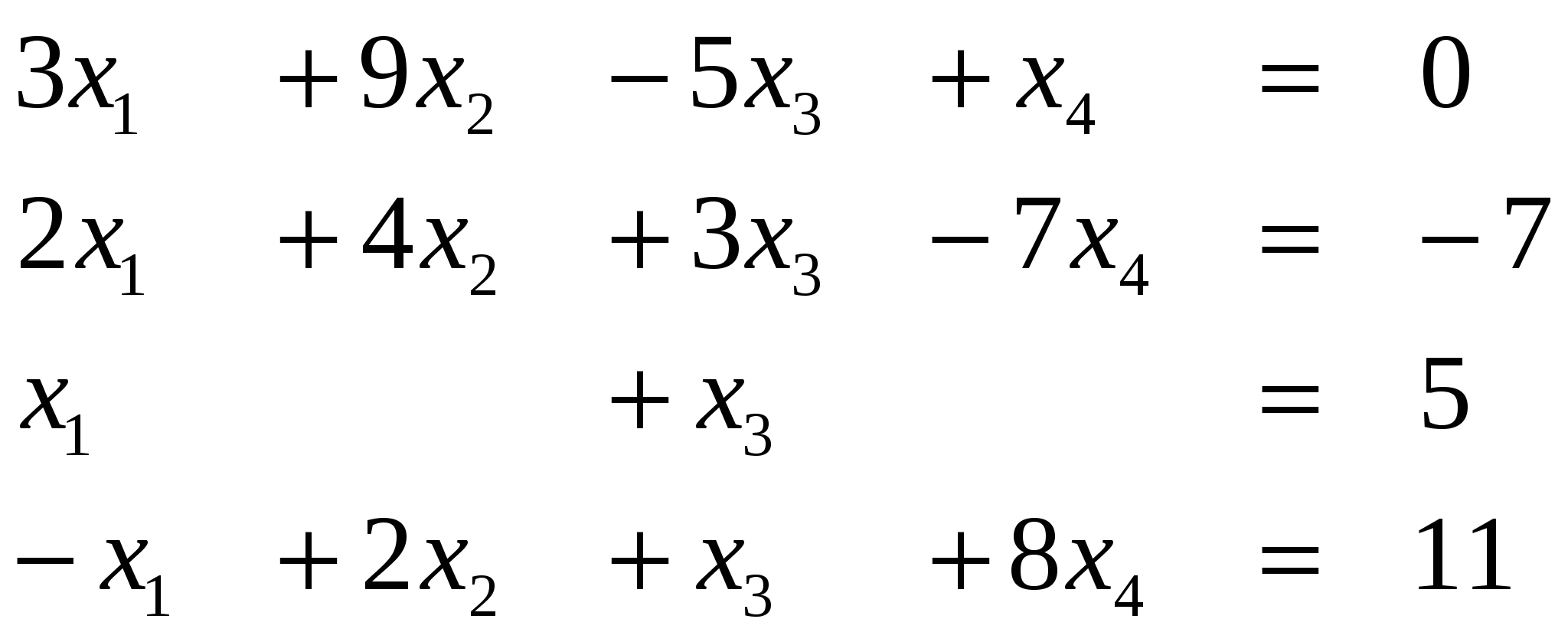
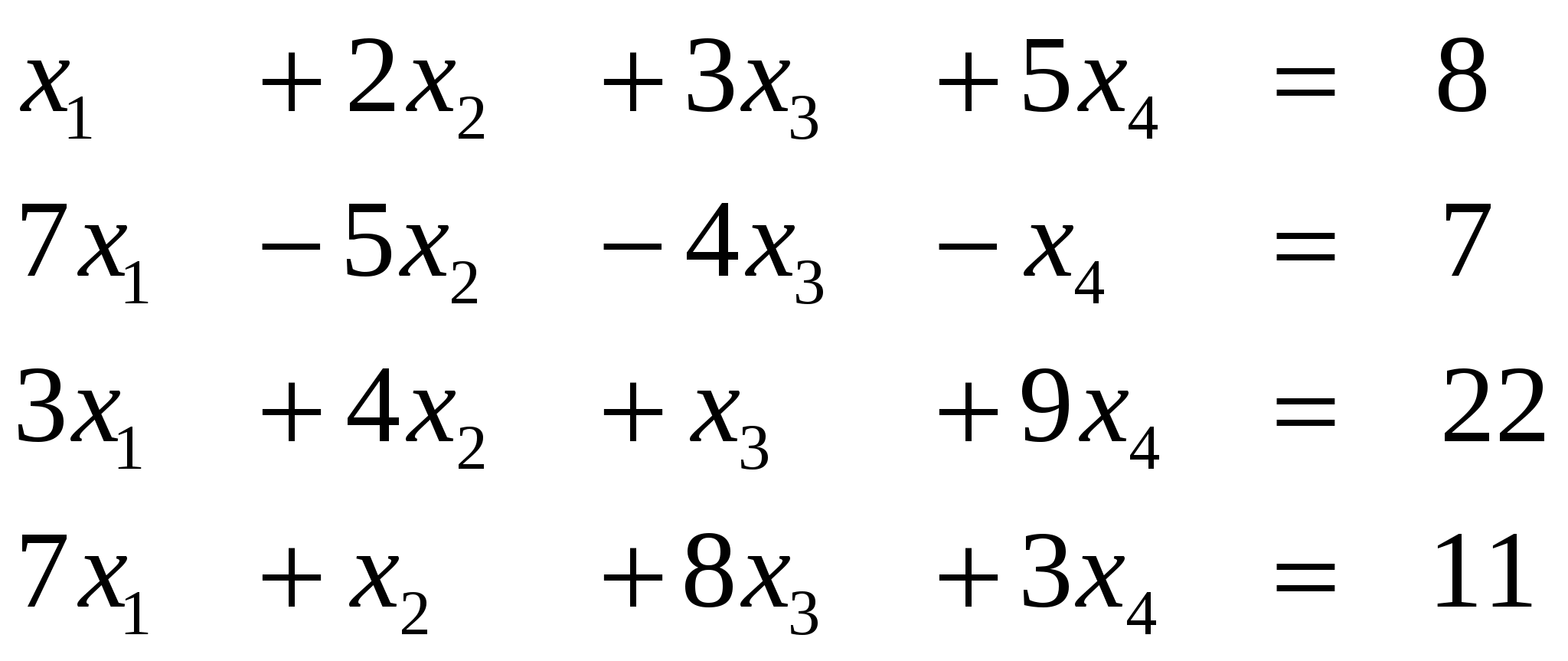
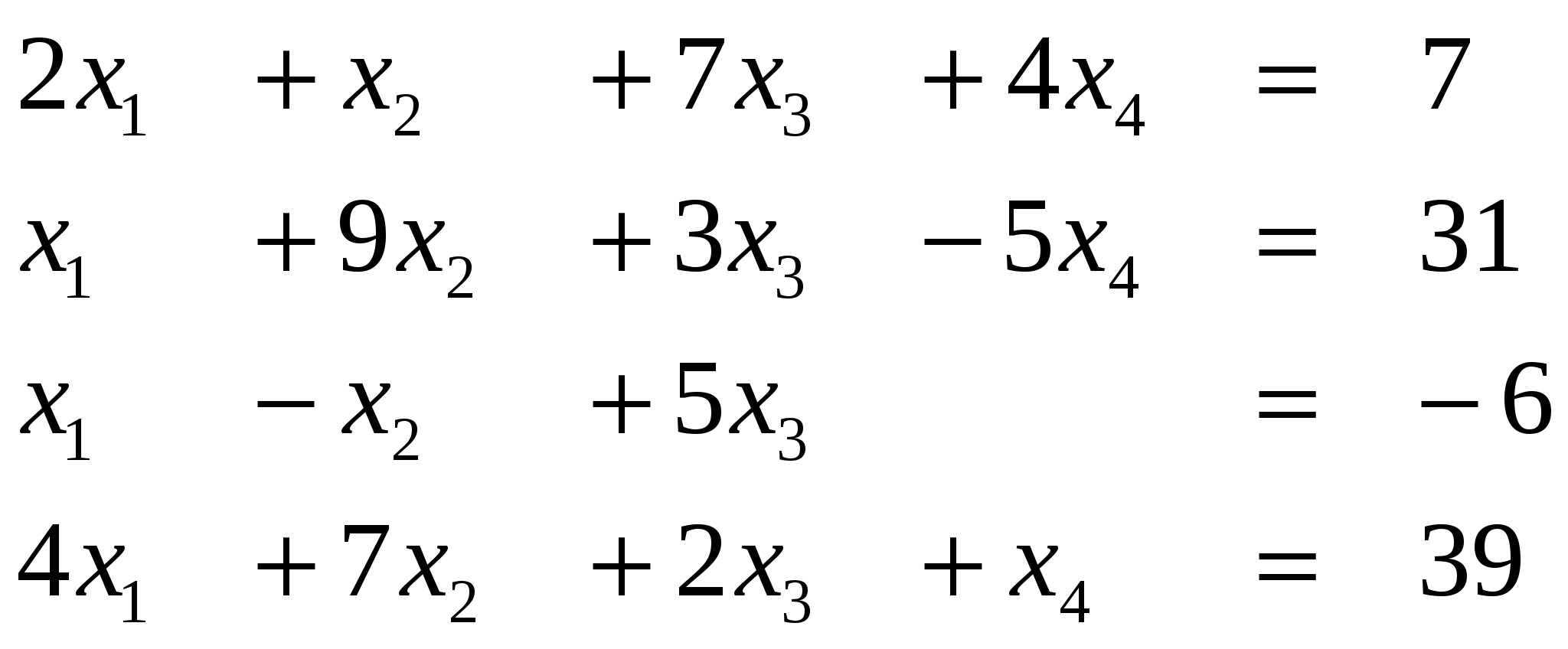
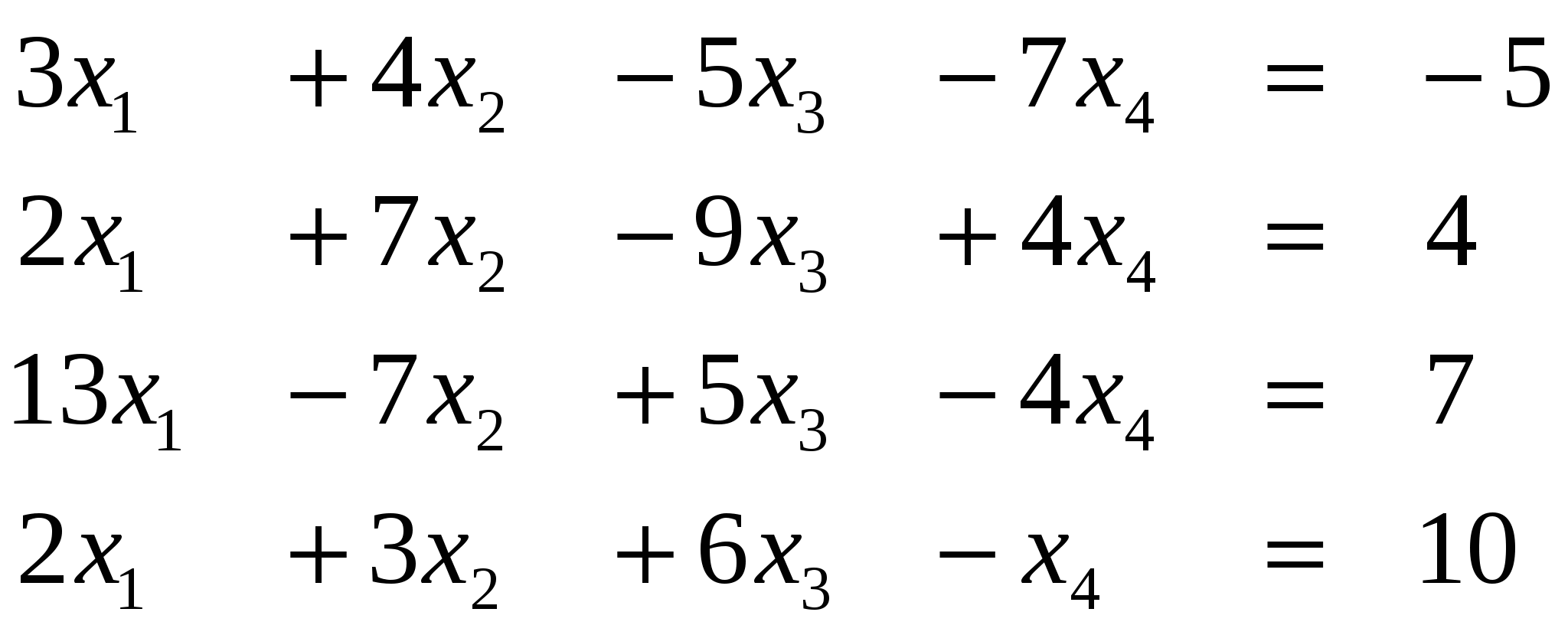
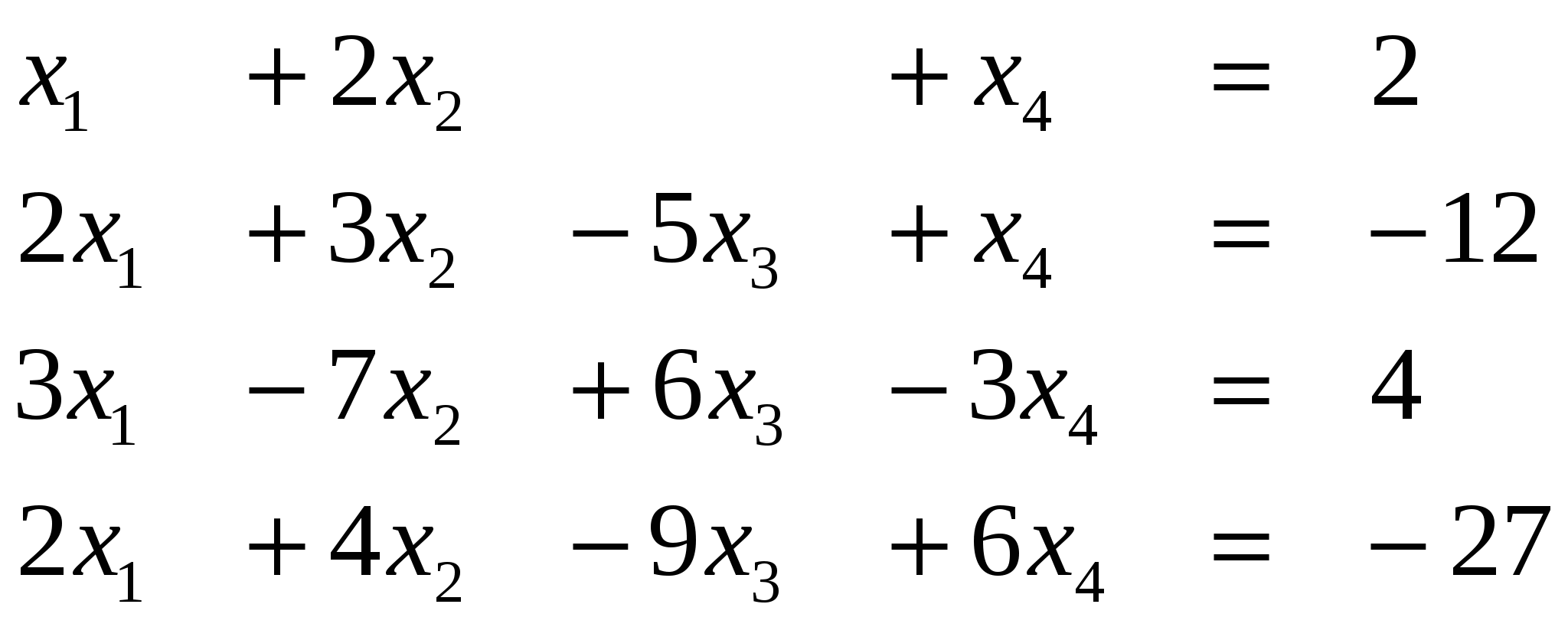
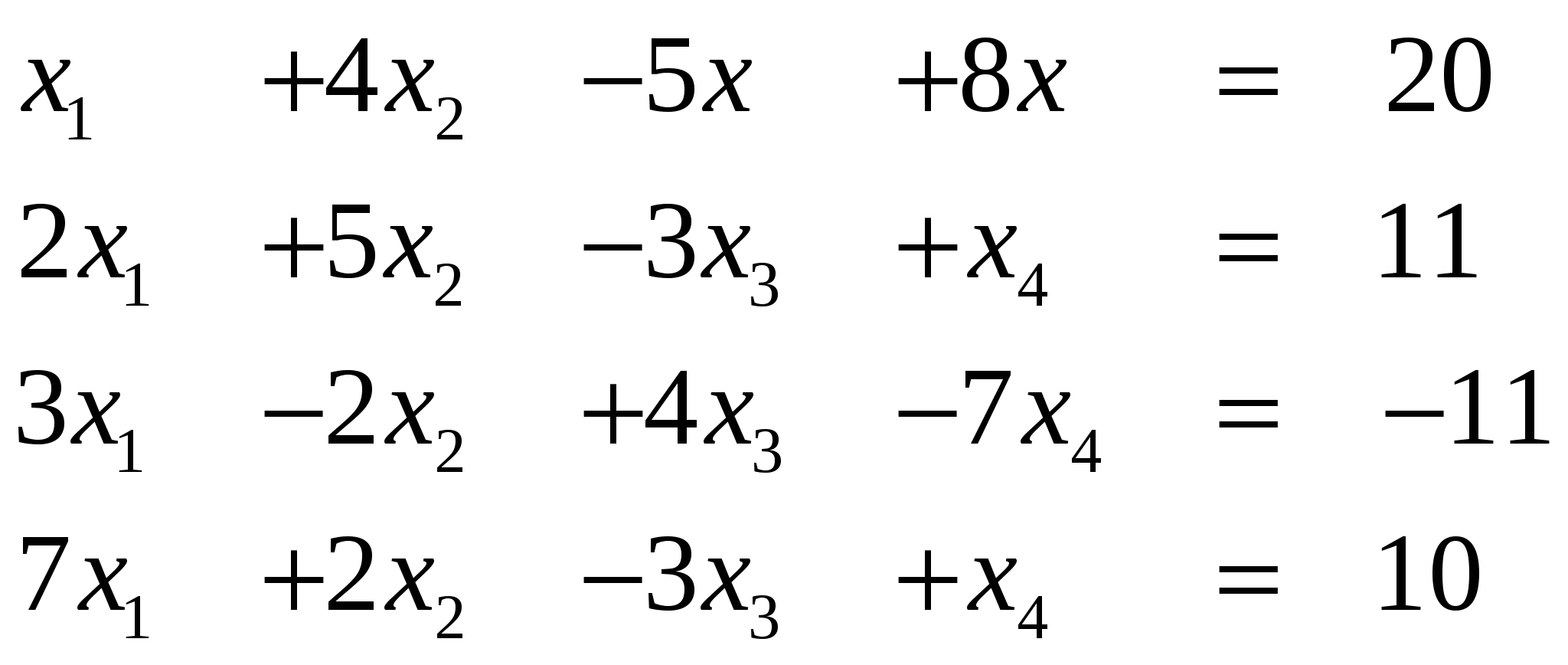
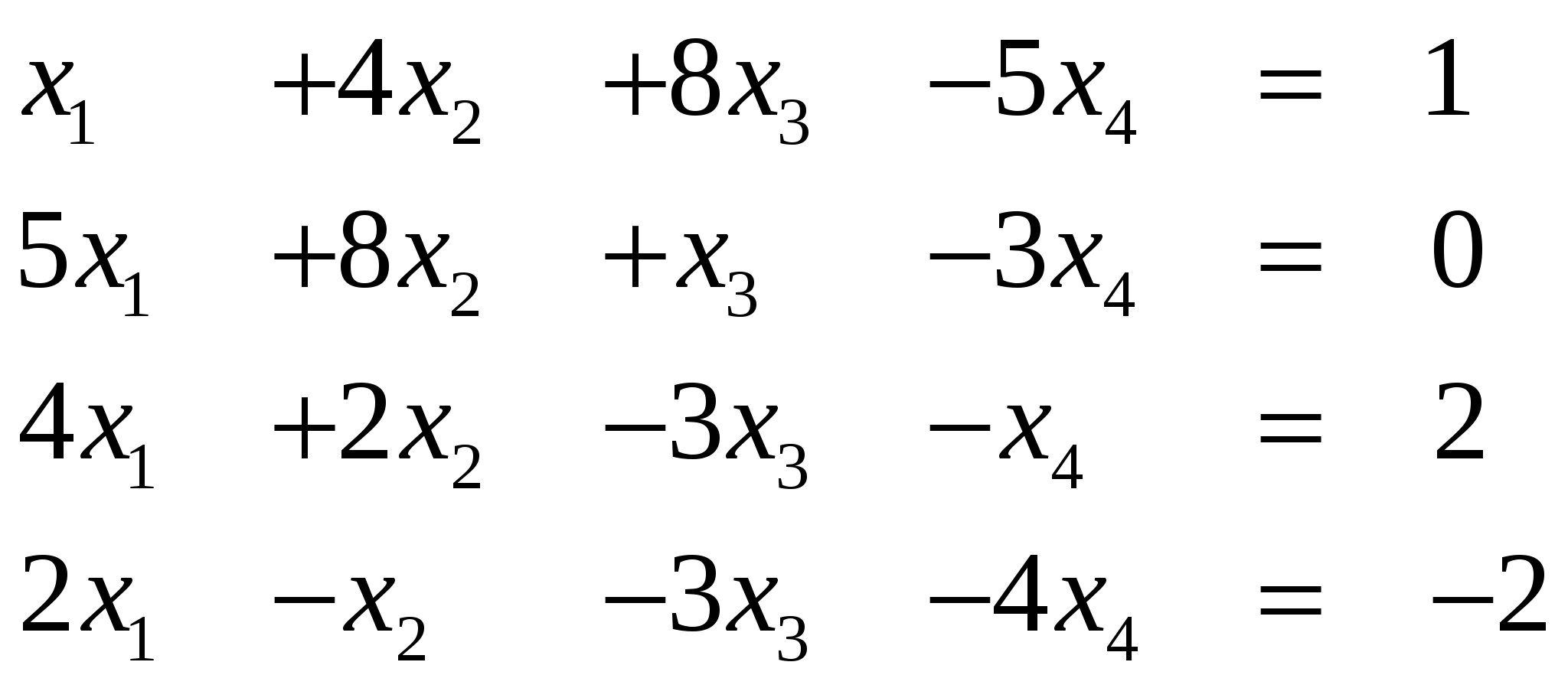
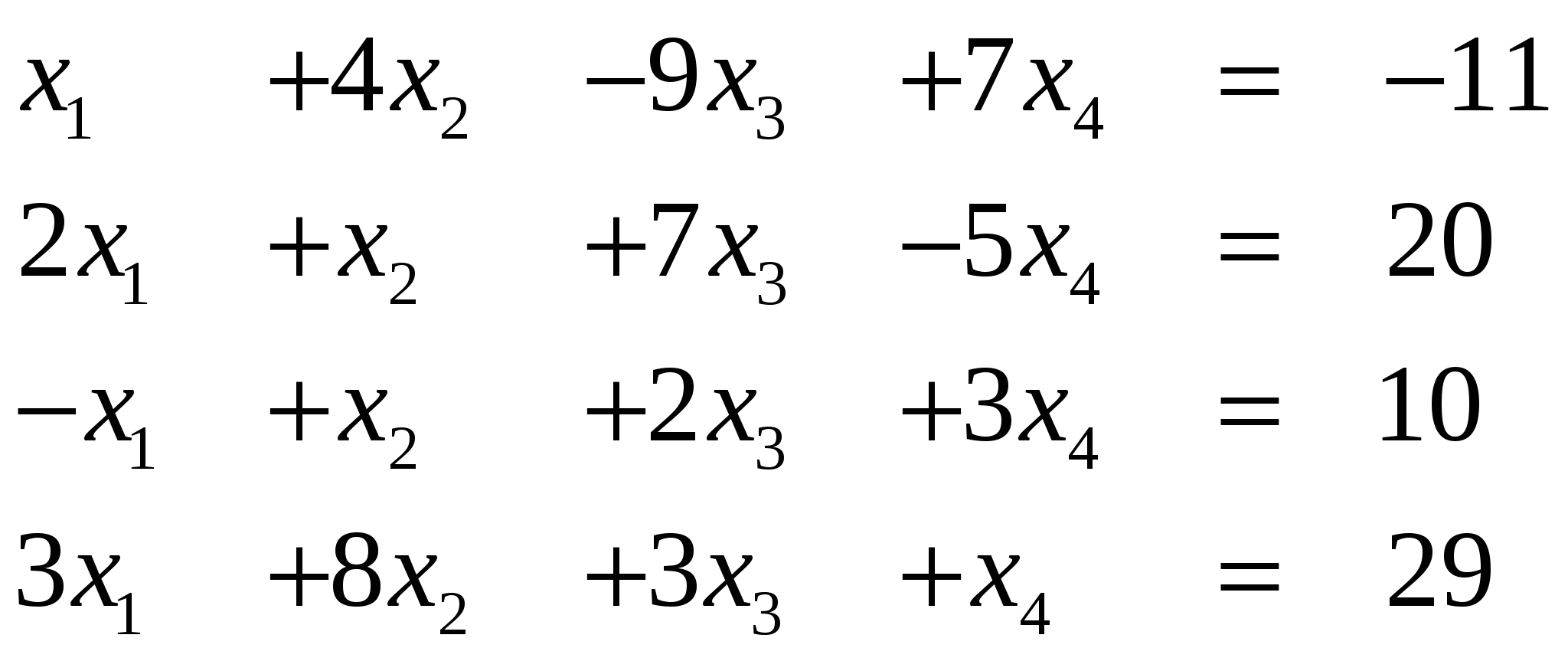
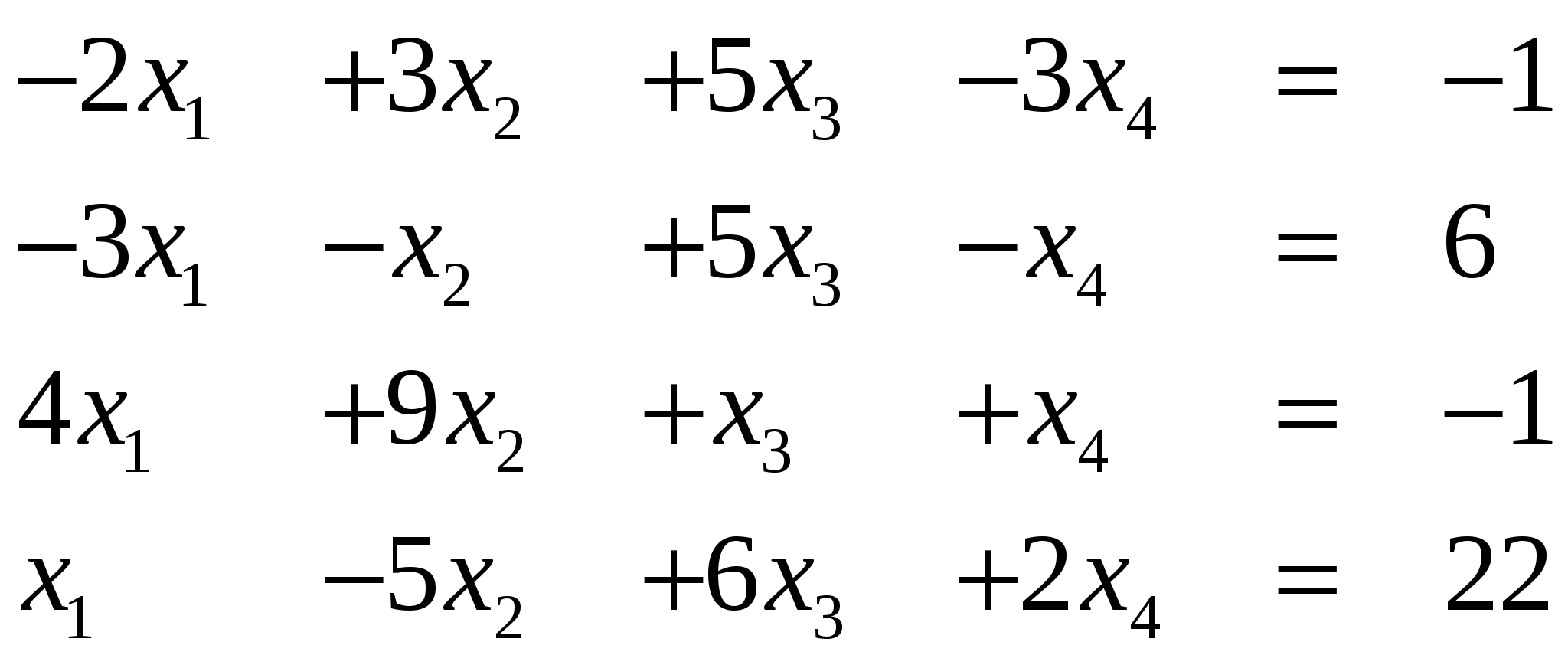
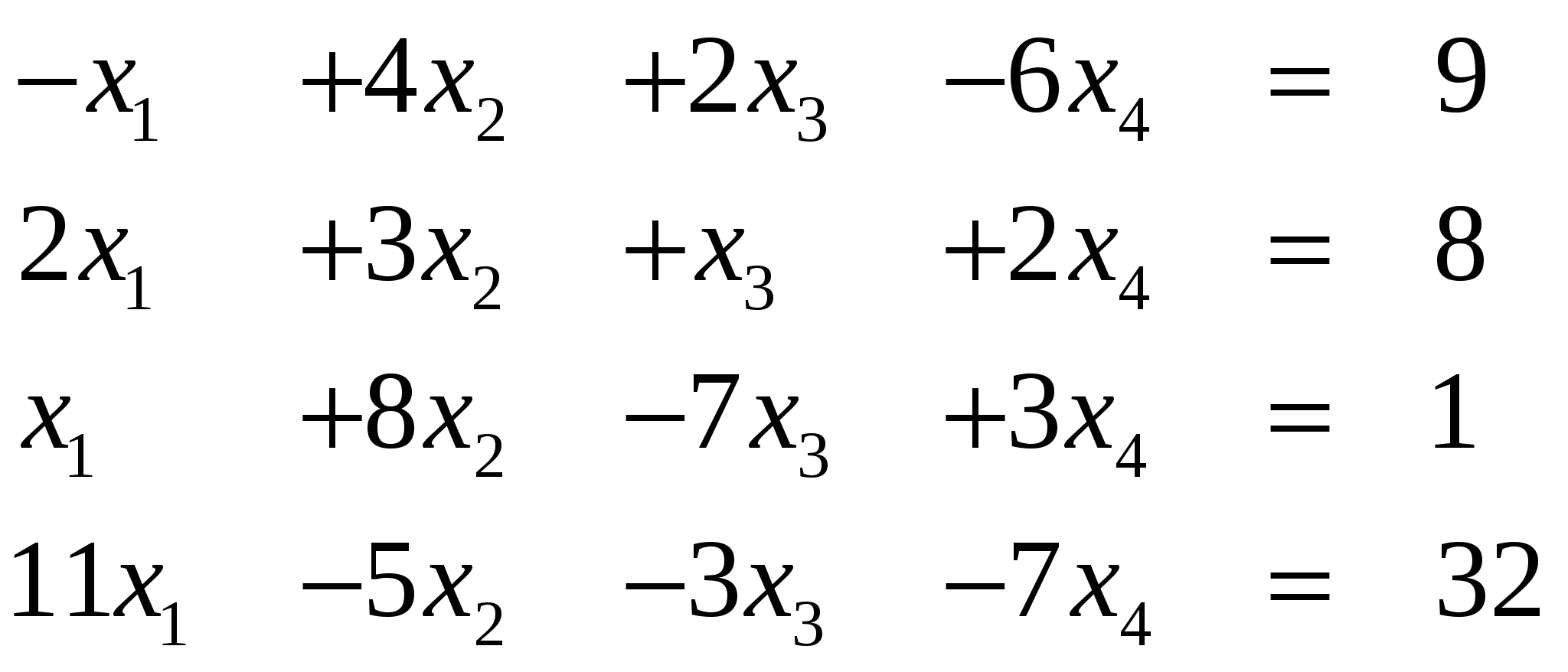
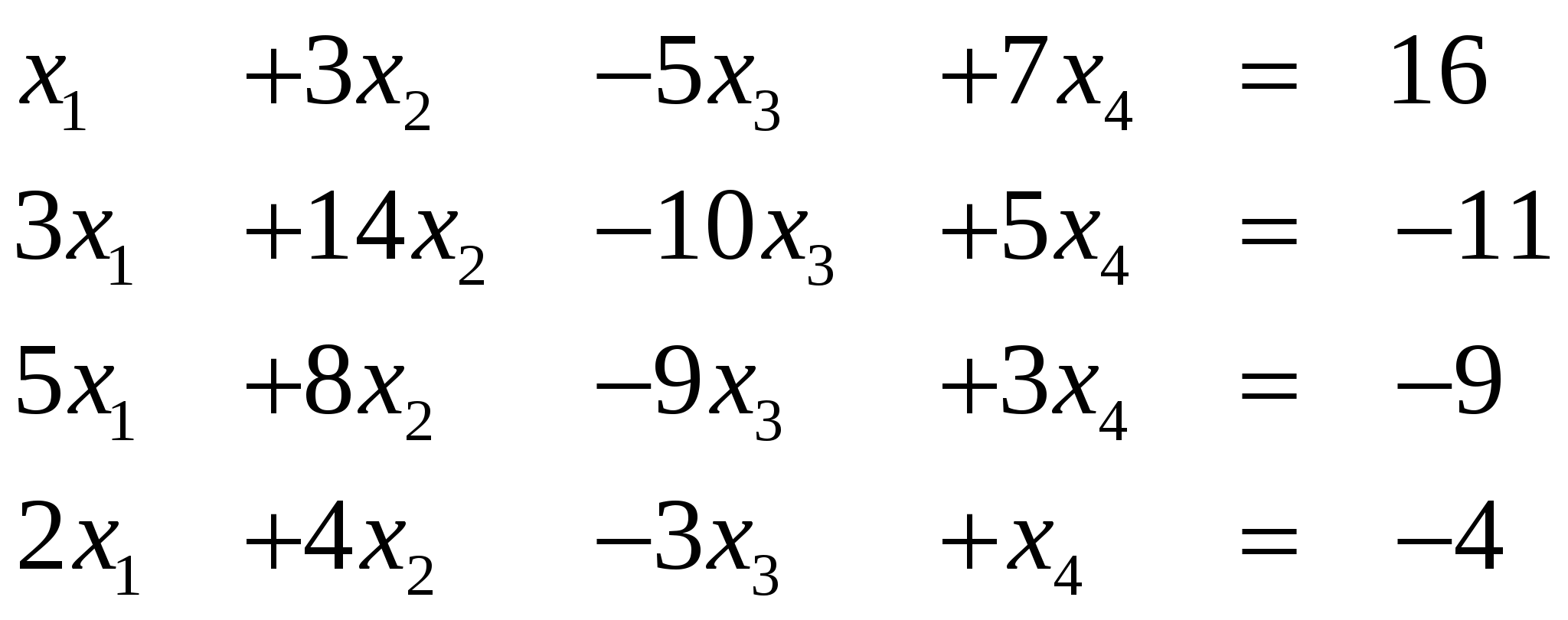 Ответ (1; ….)
Ответ (1; ….)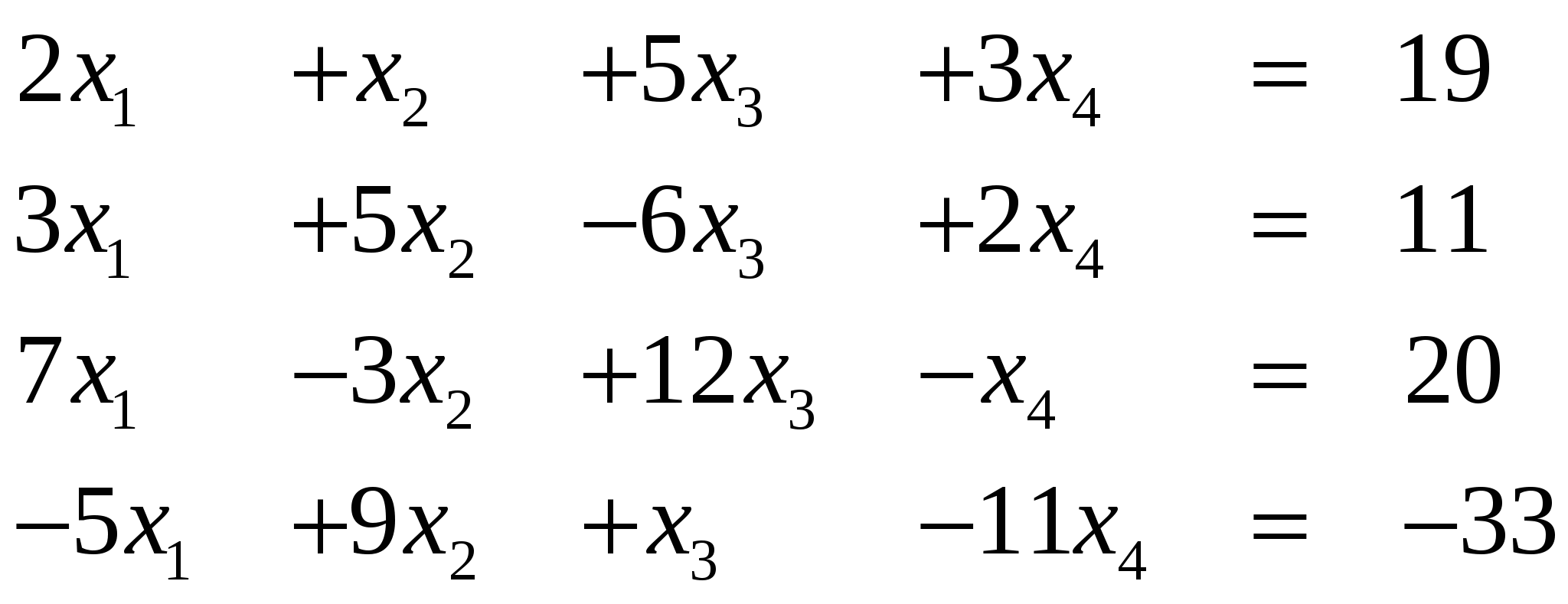 Ответ (2; ….)
Ответ (2; ….)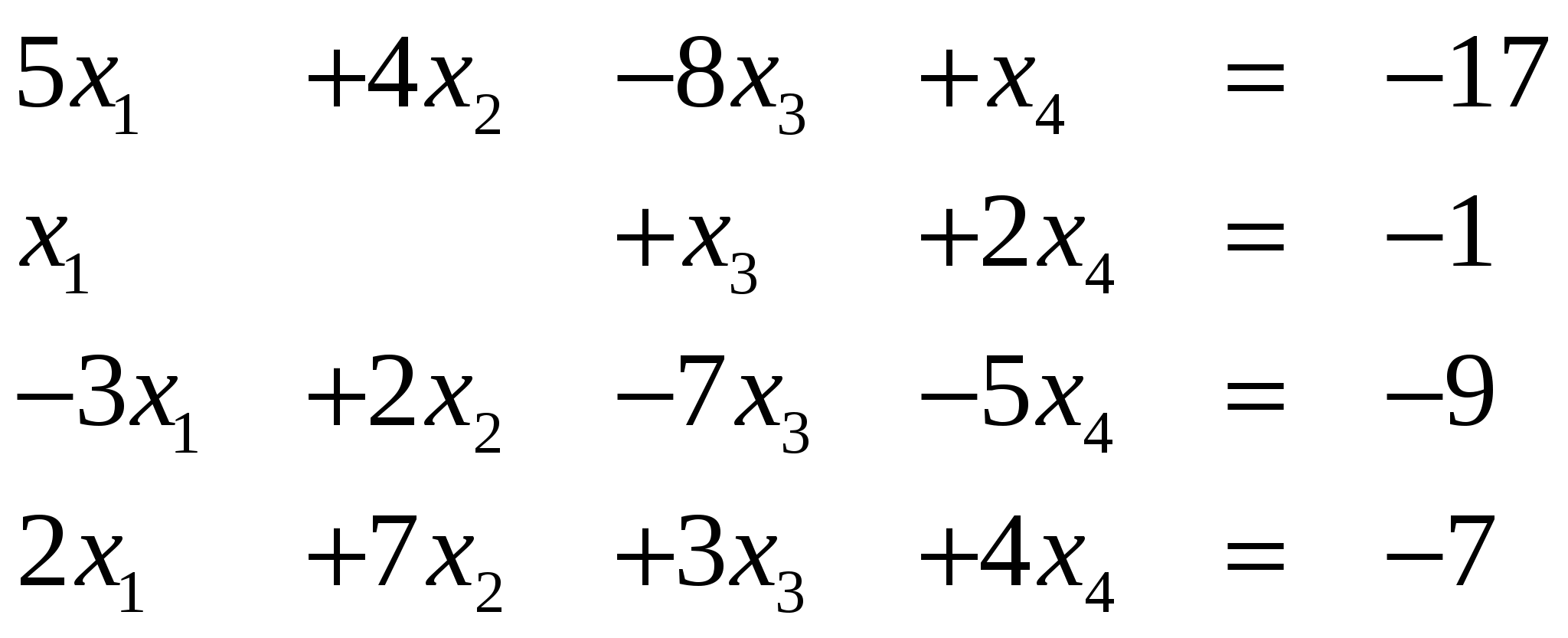 Ответ (1; ….)
Ответ (1; ….) .
. .
.




















