Лабораторная работа 2 Приближение функций 2 Лабораторная работа 7 Интерполяция функций. 7 Лабораторная работа 9

• Название: Лабораторная работа 2 Приближение функций 2 Лабораторная работа 7 Интерполяция функций. 7 Лабораторная работа 9
• Дата: 17.03.2023
• Размер: 0.93 Mb.
• Имя файла: Metod_ukaz-ya_po_labam_ChM.doc
• Тип: Лабораторная работа; #997724
• страница: 5 из 6

Лабораторная работа № 6.

Численные методы интегрирования.

Цель работы: научиться вычислять определенный интеграл на основе заданных значений подынтегральной функции различными методами.

Задание:

1. Вычислить на интеграл заданной функции на отрезке с

точностью методами трапеций и Симпсона. Сравнить точность полученных результатов.

2. Определить, какое число отрезков разбиения обеспечило бы достижение точности при вычислении заданного интеграла по формуле трапеций.

Вариант	Подынтегральная функция	Пределы интегрирования a b
1		5	6,5
2		2	3,5
3		3	3,5
4		0	2
5		0,5	2
6		2	2,5
7		0	1
8			2
9		2	5
10		0,2	0,3
11		0
12		0	2
13		0
14		1	2
15		0	1
16		0	2
17		0	1
18		0,5	1
19		0
20		0
21		0,1	0,5
22		1	2
23		0	1
24		3	4
25		0,1	0,3

Порядок выполнения работы:

Пример 1. Вычислить интеграл

по формуле трапеций, разделив отрезок

на 10 равных частей, и оценить погрешность вычислений.

Оценим ошибку метода. Для этого найдем вторую производную подынтегральной

функции:



На отрезке всюду

положительна, причем ее значение ограничено сверху:

Таким образом, используя формулу (8.7.б)

имеем: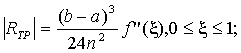



полагая , получим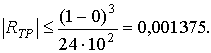

Итак, приняв на заданном участке интегрирования

мы сможем получить интеграл от заданной функции с погрешностью, не превышающей

0,001375, если будем вести вычисления таким образом, чтобы погрешность

округления не исказила окончательный результат в пределах точности метода.

В соответствии с формулой трапеций (8.3) и учетом рассчитанной ошибки получим

Пример 2. Вычислить интеграл из примера 1 по формуле Симпсона при том же

числе отрезков разбиения

Для оценки остаточного члена найдем производную четвертого порядка от

подынтегральной функции



Значение на отрезке

ограничено числом 14. Используя формулу (8.7.в), получаем оценку: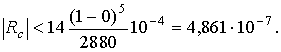



Приведем полученный результат в соответствии с оценкой



Сравнивая этот результат со значением интеграла, полученным в примере 1,

заметим, что при одинаковом числе отрезков разбиения формула Симпсона дает

ответ с большим числом верных знаков.

Посмотрим, как можно было бы воспользоваться в данном случае формулой (8.7.в).

Пусть требуется найти значение заданного интеграла с точностью

Тогда по формуле (3.7.в) получим: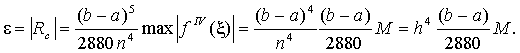




Отсюда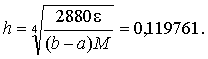



Следовательно, для достижения точности достаточно было разбить отрезок

на 9 частей.