Лабораторная работа 2 Приближение функций 2 Лабораторная работа 7 Интерполяция функций. 7 Лабораторная работа 9
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
Лабораторная работа № 3.Построение сплайн-функции.Цель работы: Изучить интерполяцию сплайн-функциями, научиться строить сплайны для функции, заданной таблично. Задание: По заданной таблице значений составить линейный, параболический и кубический сплайны ( и вычислить, используя проверочную функцию). В одной системе координат построить график функции и графики всех сплайнов. Сделать анализ представленных методов. Решение: Сплайном называется непрерывная функция, принимающая в узлах интерполяции соответствующие значения и описываемая на отдельных отрезках ( ) некоторыми полиномами невысокого порядка (обычно второго или третьего). Сплайны хороши тем, что дают возможность получить приближенный аналитический вид функции, при этом степень полинома остается невысокой. Главным недостатком сплайнов является то, что на каждом интервале функция приближается отдельным полиномом. Таким образом, для всего промежутка требуется построить полином. При увеличении степени сплайна повышается точность интерполяции, однако, увеличивается количество вычислений и порядок полинома. Простейшим случаем сплайн-функции является линейный сплайн, получающийся соединением точек …, ломаной линией. В этом случае где коэффициенты и можно найти по формулам: Параболический сплайн строится на полиномах второго порядка . При построении параболического сплайна обычно считается заданной производная функции в первом узле . Коэффициенты полиномов такого сплайна могут быть вычислены по следующим рекуррентным формулам: 1) 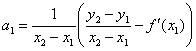 i) 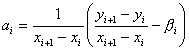 где Чаще всего на практике используют кубический сплайн, так как при достаточно низком порядке полиномов он дает удовлетворительную точность вычислений. Для полиномов кубического сплайна коэффициенты могут быть получены по следующей рекуррентной схеме: 1) 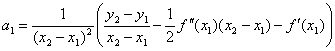 где значения и считаются заданными (на практике часто полагают ) i) 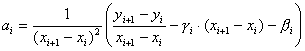 где , Лабораторная работа № 4.Численные методы решения нелинейных уравнений.Цель работы: Изучить численные методы решения нелинейных уравнений с одним неизвестным; научиться программировать алгоритмы итерационных методов уточнения корней; сравнить скорость сходимости различных методов. Задание 1. Графическим методом определить наличие, приблизительное расположение и количество корней заданных уравнений. 2. Задать границы отрезка (интервала поиска). Значение шага поиска взять в пределах . Результаты представить в виде таблицы:
3. Уточнить корни уравнений по методу половинного деления. В качестве начального отрезка использовать интервал, найденный при выполнении второго задания. Определить приближенные значения корней с разной точностью (например, , , ). Результаты представьте в виде таблицы:
4. Найти корень по методу Ньютона (методу касательных). В качестве начального приближения к корню выберите одну из границ интервала, найденного в ходе выполнения второго задания. Для правильного выбора начального приближения используйте критерий . Определите приближенные значения корней с разной точностью (например, , , ). Результаты представьте в виде таблицы:
5. Уточнить значение корня по методу секущих. В методе секущих необходимо задать два приближения к корню – нулевое и первое . Нулевое приближение выбирается аналогично методу Ньютона. В качестве первого приближения можно взять величину: . Результаты представить в виде аналогичной таблицы. 6. Уточнить значение корня по методу простых итераций. В программе предусмотрите счетчик количества итераций, совершаемых для достижения заданной точности. В качестве начального приближения к корню выберите любую точку из интервала , найденного при выполнении задания 2. Определить приближенные значения корней с разной точностью (например, , , ). Результаты представить в виде, аналогичном заданию 4. Пояснения. Преобразуйте исходное уравнение к виду, подходящему для метода простых итераций, т.е. к виду . Проверьте основное условие сходимости метода: для средней точки интервала . При невыполнении условия найдите другой способ перехода от исходного уравнения к уравнению в итерационной форме или запишите уравнение в виде и выбором константы обеспечьте выполнение условия сходимости. Проведите анализ результатов. Составьте сводную таблицу (для выбранной точности, например ):
На основе таблицы сформулировать выводы о скорости сходимости различных методов. Отчет Отчет о выполнении работы состоит из двух частей: теоретической и практической. В первой части отчета необходимо привести краткое описание и характеристики использованных методов (рабочая формула, условия сходимости, критерии применимости). Во второй части отчета должны быть представлены результаты выполнения практических заданий для каждого уравнения. Должны быть приведены графики, поясняющие процесс локализации корней, подробно отражены выбор начального приближения в методе Ньютона и проверка сходимости метода простых итераций, а также приведены таблицы с результатами. В заключении необходимо сделать анализ результатов и сформулировать выводы. К отчету должны быть приложены расчёты. Таблица 1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
