Контрольная по статистике. Статистика 2 вариант исправленный. Средние показать на графике, сделать выводы
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
Задача 1. Сгруппировать приведенные в таблице 2.1 данные о суточном производстве продукции в виде дискретного ряда распределения, представить результаты группировки в виде таблицы и графика, оформив его по ГОСТу. Рассчитать среднюю арифметическую, среднюю квадратическую, среднюю прогрессивную повышающую, среднюю прогрессивную понижающую, среднюю кубическую, среднюю антигармоническую, моду и медиану. Средние показать на графике, сделать выводы. Рассчитать показатели вариации (размах абсолютный и относительный, среднее линейное и среднее квадратическое отклонение абсолютное и относительное, дисперсию. Сделать выводы и представить показатели вариации на графике, оформив его по стандарту. Таблица 2.1 – Исходные данные о суточном производстве
Решение Постоим дискретный ряд распределения. Таблица 1.1 – Группировка суток в зависимости от объема производства
По данным вариационного ряда построим полигон частот (рис. 1.1) 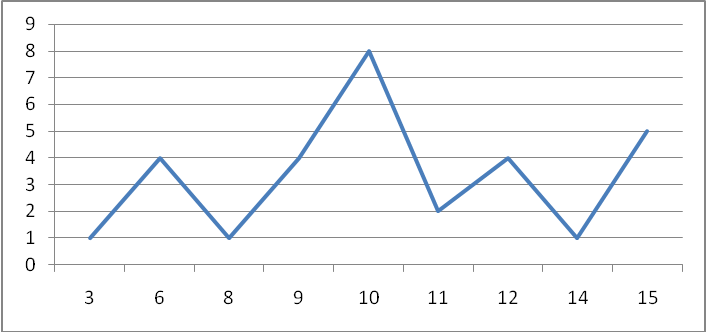 Рис. 1.1. Полигон распределения суточного производства продукции Рассчитаем среднюю арифметическую, среднюю квадратическую, среднюю прогрессивную повышающую, среднюю прогрессивную понижающую, среднюю кубическую, среднюю антигармоническую, моду и медиану. Таблица 1.2 – Определение средних величин
Расчет средних:
Мода – это наиболее часто встречающийся вариант ряда. Максимальная частота равна 8, следовательно, модальное значение признака равно 10: fmax = 8 → Мо = 10 Медиана – это значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. т.е. медианное значение признака соответствует номерам 15 и 16. Накопленная частота 16 впервые превышает 15,5, следовательно, медиана равна 10. У половины единиц совокупности значение признака не превышает 10, у половины не меньше его. 2) Рассчитаем показатели вариации (размах абсолютный и относительный, среднее линейное и среднее квадратическое отклонение абсолютное и относительное, дисперсию). Таблица 1.3 – Исходные и расчетные данные для определения показателей вариации
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

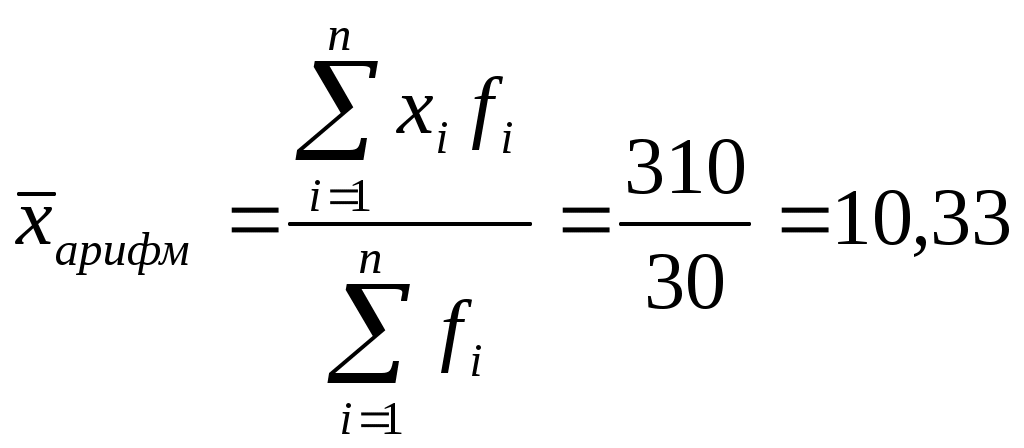 (1.1)
(1.1)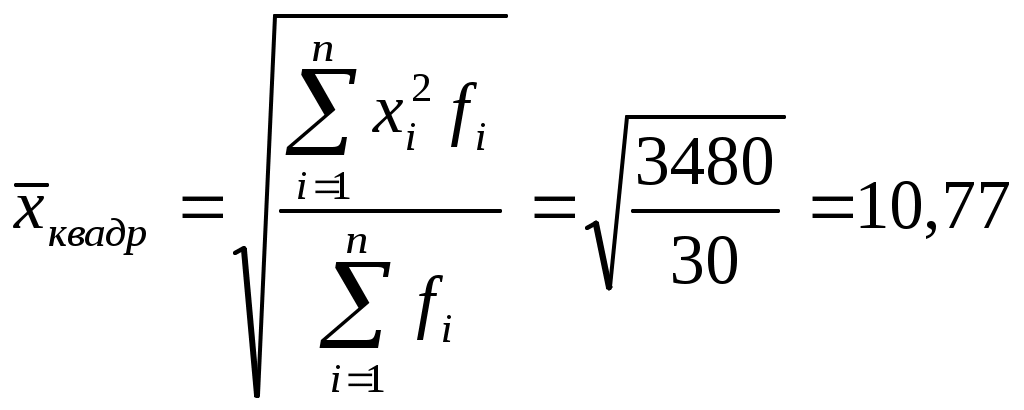 (1.2)
(1.2)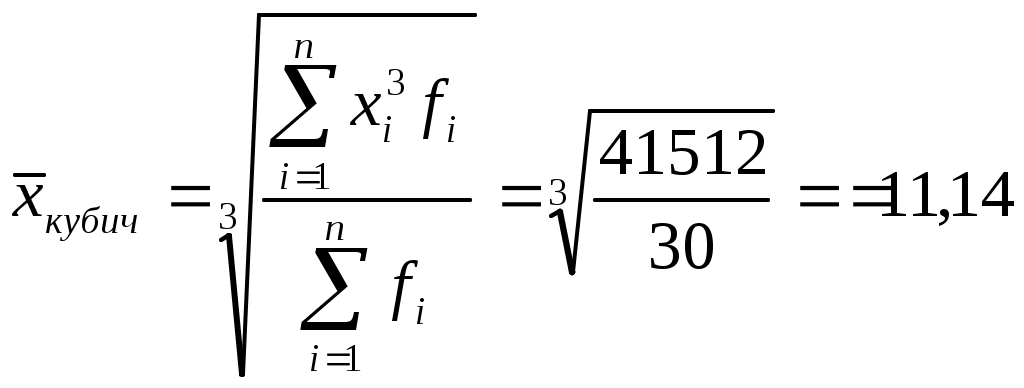 (1.5)
(1.5)