Контрольная по статистике. Статистика 2 вариант исправленный. Средние показать на графике, сделать выводы
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
Решение а) Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d,называется арифметической прогрессией. Число d называется разностью прогрессии. Любой член арифметической прогрессии вычисляется по формуле (5.1): an = a1 + d ( n – 1 )(5.1) Следовательно, используя данные за начальный и конечный период можно вычислить d. 1100 = 1020 + d (5 - 1); d = 20 В основе методики определения неизвестных значений ряда динамики лежит использование такого показателя, как цепной абсолютный прирост: Оформим в виде таблицы 5.1 искомые значения ряда динамики: Таблица 5.1 – Себестоимость, руб./т.
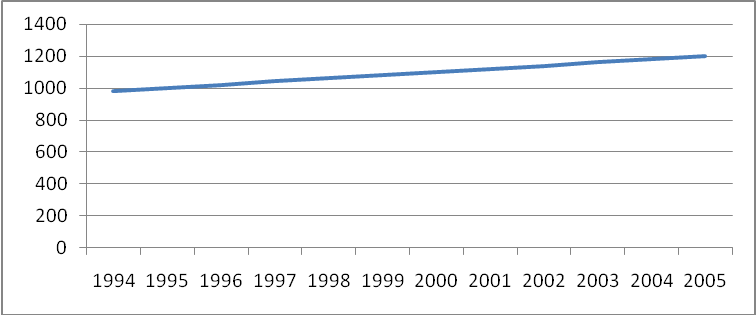 Рис. 5.1. Себестоимость, руб./т. б) Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q, называется геометрической прогрессией. Число q называется знаменателем прогрессии. Любой член геометрической прогрессии вычисляется по формуле (5.2): bn = b1 q n - 1 (5.2) Следовательно, используя данные за начальный и конечный период можно вычислить q. 1100 = 1020 × q4, q = 1,01906 В основе методики определения неизвестных значений ряда динамики лежит использование такого показателя, как цепной коэффициент роста: Оформим в виде таблицы 5.2 искомые значения ряда динамики: Таблица 5.2 – Расчет себестоимости, руб./т.
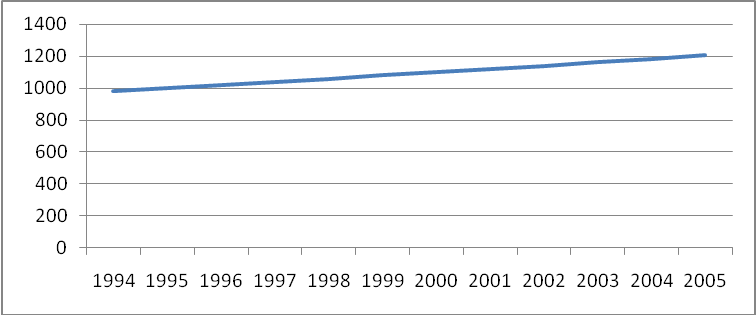 Рис. 5.2. Себестоимость, руб./т. На рис. 5.1. изображен ряд динамики, в котором значении ряда изменяются в арифметической прогрессии, на рис. 5.2. – в геометрической. Задача 6. Произвести выравнивание ряда динамики методом двух полусредних и скользящей средней простой. Группы сформировать по четыре значения и сдвигаться на 2 значения. Изобразить на графике эмпирический и выровненный ряды, сделать вывод о динамике суточной выработки к концу месяца по данным таблицы 2.6. Таблица 2.6 – Исходные данные
Решение В методе двух полусредних совокупность делится пополам. Для каждой половины рассчитывается средняя арифметическая. Если х1 > x2, то имеем тенденцию спада, а если х1 < x2, то имеем тенденцию роста. Талица 6.1 – Исходные данные для расчета двух полусредних
В исходных данных х1 > x2, следовательно, имеется тенденция спада суточного производства. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень ряда из такого же числа уровней, начиная со второго (если скольжение идет по 1 значению), далее – начиная с третьего и т.д. Таблица 6.2 – Исходные и расчетные данные
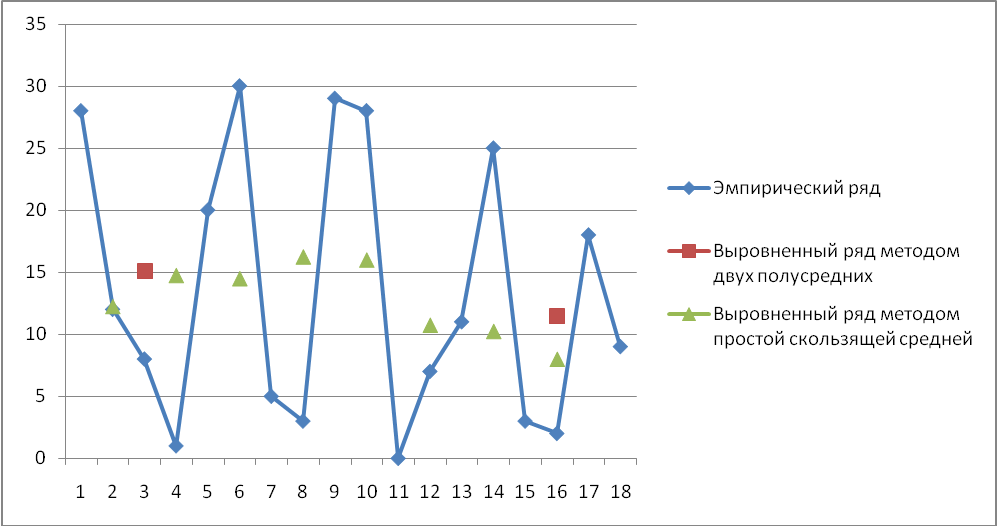 Рис. 6.1 Динамика суточного производства Судя по эмпирическим данным, простой скользящей средней и метода полусредних, динамика суточной выработки к концу месяца имеет тенденцию к понижению. Задача 7. Исследовать зависимость расходов по переделу (у) от объема продукции (х) по данным таблицы 2.7 и таблицы 2.8: Построить поле корреляции; Построить эмпирическую линию с соответствующим объяснением, Определить форму связи; Оценить тесноту связи; Проверить коэффициент корреляции на достоверность; Рассчитать коэффициенты регрессии и построить теоретическую линию; Рассчитать и построить доверительные пределы отклонения, приняв t=2, 04 для р=0, 95; Сделать оценку предсказательной силы модели по остаточной дисперсии. По желанию можно сделать проверку по критерию Фишера, приняв итабл=1, 96 при р=0, 95; Рассчитать долю условно-постоянных затрат в расходах по переделу. Сделать выводы. Таблица 2.7 – Значения объема производства
Таблица 2.8 – Расходы по переделу, тыс. руб.
|
