Решение
Построить поле корреляции
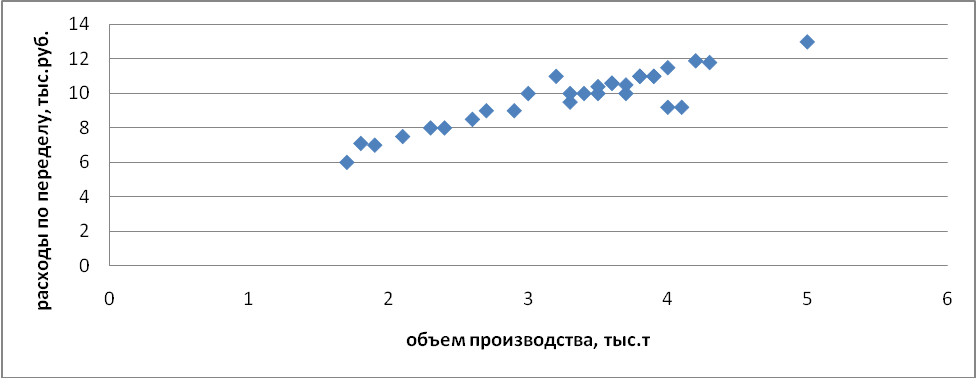
Рис. 7.1. График корреляционного поля
Построить эмпирическую линию с соответствующим объяснением.
Эмпирическая линия отражает основную тенденцию рассматриваемой зависимости. Если эмпирическая линия по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи между признаками.
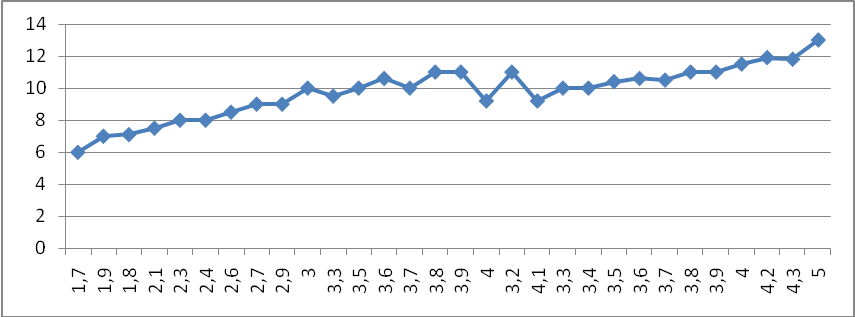
Рис. 7.2. Эмпирическая линия
По форме зависимости данная связь является линейной, а по направлению связи – положительной (прямой), так как с увеличением объемов производства происходит увеличение расходов по переделу.
Оцениваем тесноту связи с помощью коэффициента корреляции
Таблица 7.1 – Исходные и расчетные данные
Порядковый номер данных, i
|
Объем производства, тыс.т. (xi)
|
Значение расходов по переделу (yi)
|
xiyi
|
xi2
|
yi2
|
1
|
1,7
|
6
|
10,2
|
2,89
|
36
|
2
|
1,9
|
7
|
13,3
|
3,61
|
49
|
3
|
1,8
|
7,1
|
12,78
|
3,24
|
50,41
|
4
|
2,1
|
7,5
|
15,75
|
4,41
|
56,25
|
5
|
2,3
|
8
|
18,4
|
5,29
|
64
|
6
|
2,4
|
8
|
19,2
|
5,76
|
64
|
7
|
2,6
|
8,5
|
22,1
|
6,76
|
72,25
|
8
|
2,7
|
9
|
24,3
|
7,29
|
81
|
9
|
2,9
|
9
|
26,1
|
8,41
|
81
|
10
|
3
|
10
|
30
|
9
|
100
|
11
|
3,3
|
9,5
|
31,35
|
10,89
|
90,25
|
12
|
3,5
|
10
|
35
|
12,25
|
100
|
13
|
3,6
|
10,6
|
38,16
|
12,96
|
112,36
|
14
|
3,7
|
10
|
37
|
13,69
|
100
|
15
|
3,8
|
11
|
41,8
|
14,44
|
121
|
16
|
3,9
|
11
|
42,9
|
15,21
|
121
|
17
|
4
|
9,2
|
36,8
|
16
|
84,64
|
18
|
3,2
|
11
|
35,2
|
10,24
|
121
|
19
|
4,1
|
9,2
|
37,72
|
16,81
|
84,64
|
20
|
3,3
|
10
|
33
|
10,89
|
100
|
21
|
3,4
|
10
|
34
|
11,56
|
100
|
22
|
3,5
|
10,4
|
36,4
|
12,25
|
108,16
|
23
|
3,6
|
10,6
|
38,16
|
12,96
|
112,36
|
24
|
3,7
|
10,5
|
38,85
|
13,69
|
110,25
|
25
|
3,8
|
11
|
41,8
|
14,44
|
121
|
26
|
3,9
|
11
|
42,9
|
15,21
|
121
|
27
|
4
|
11,5
|
46
|
16
|
132,25
|
28
|
4,2
|
11,9
|
49,98
|
17,64
|
141,61
|
29
|
4,3
|
11,8
|
50,74
|
18,49
|
139,24
|
30
|
5
|
13
|
65
|
25
|
169
|
Итого
|
99,2
|
293,3
|
1004,9
|
347,28
|
2943,7
|
Коэффициент корреляции:
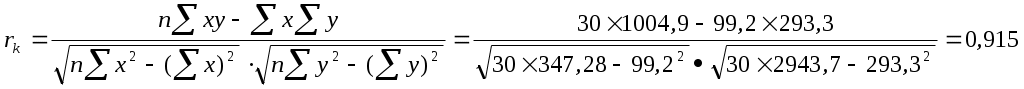 (7.1) (7.1)
Исходя из значения коэффициента корреляции, можно сделать следующие выводы:
-
- связь корреляционная
|
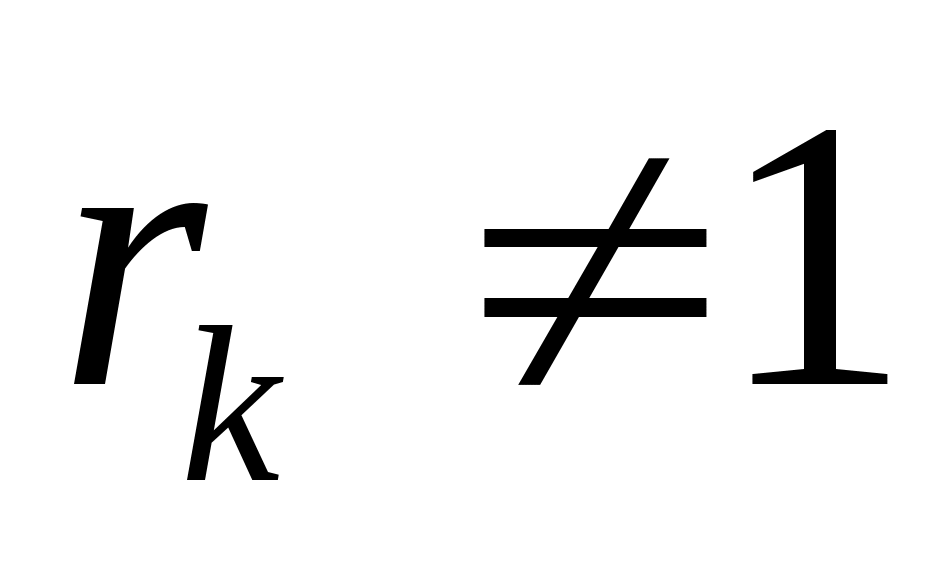
|
- связь линейная
|
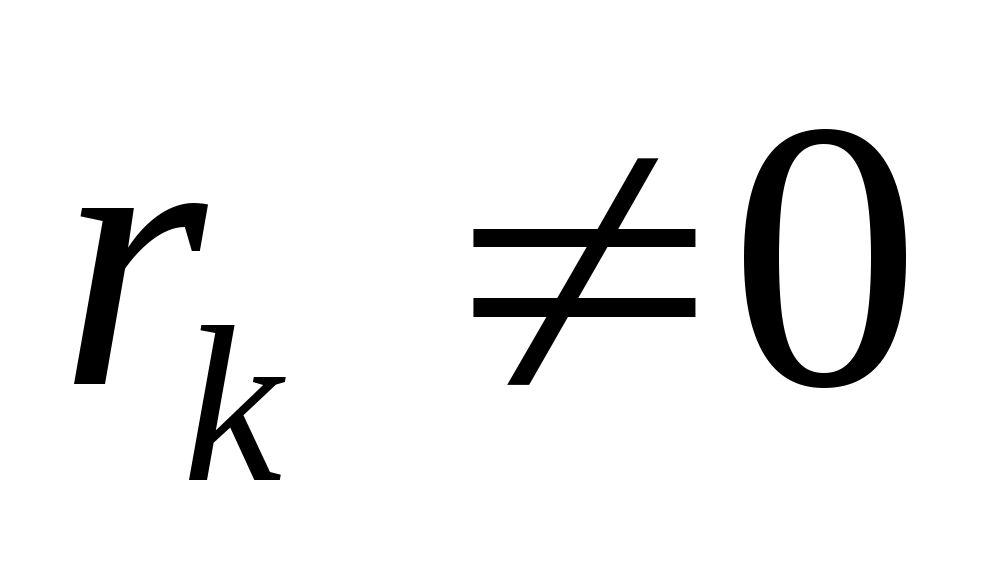
|
- связь прямо пропорциональная
|
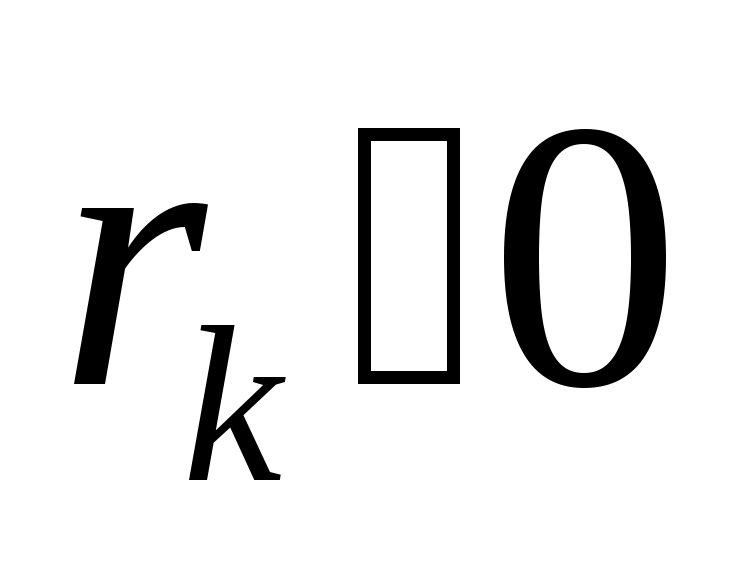
|
- связь очень тесная
|
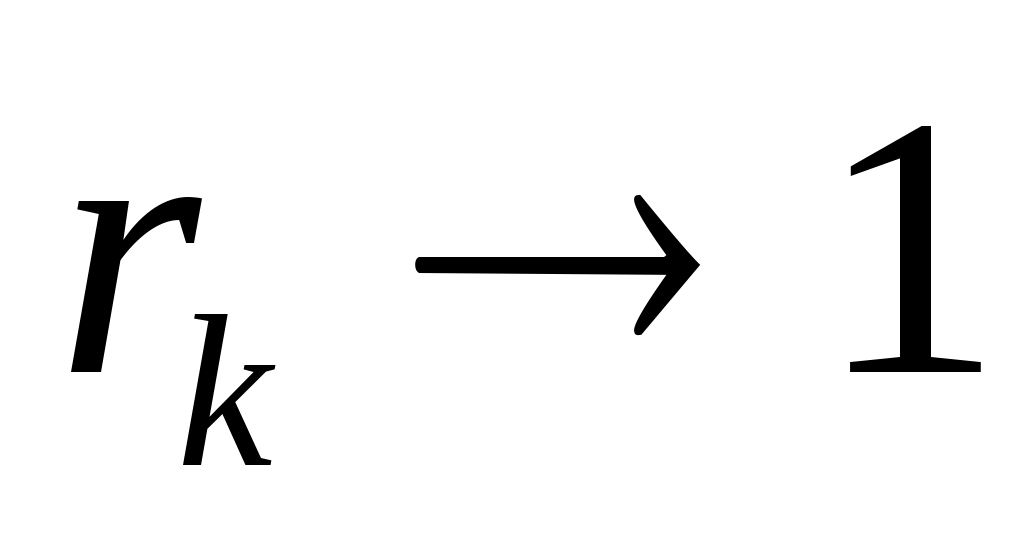
|
Проверим коэффициент корреляции на достоверность:
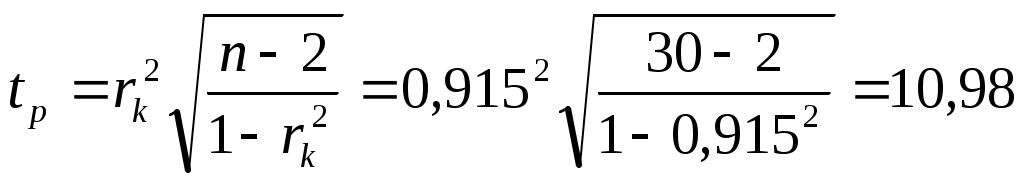 (7.2) (7.2)
Полученный расчетный коэффициент значимости больше табличного, следовательно, коэффициент корреляции достоверен.
6) Рассчитаем коэффициенты регрессии и построим теоретическую линию.
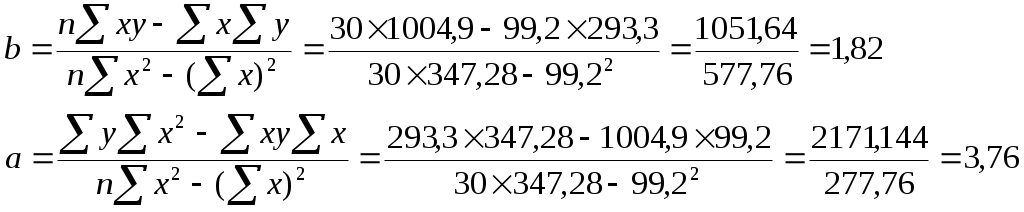 (7.3) (7.3)
(7.4)
Рассчитанные коэффициенты регрессии подставляем в уравнение корреляционной линии между объемом производства и расходами по переделу.
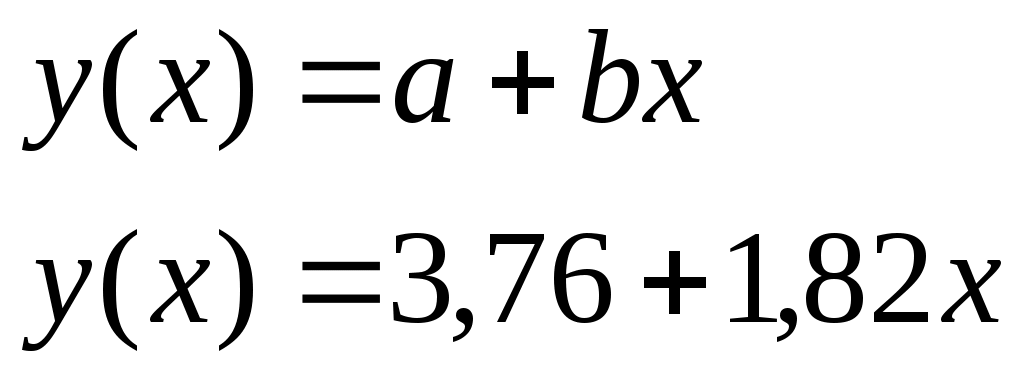 (7.5) (7.5)
Строим прямую на поле корреляции по двум точкам, например A(2;7,4) и B(5;13,01)
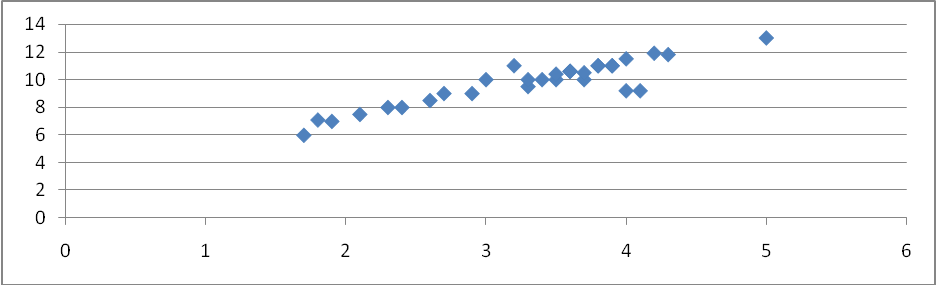
Рис. 7.3. Поле корреляции и теоретическая линия
7) Рассчитаем и постоим доверительные пределы отклонения, приняв t=2,04 для р=0,95. Графически доверительные интервалы представляют собой параллельные прямые построенной теоретической линии:
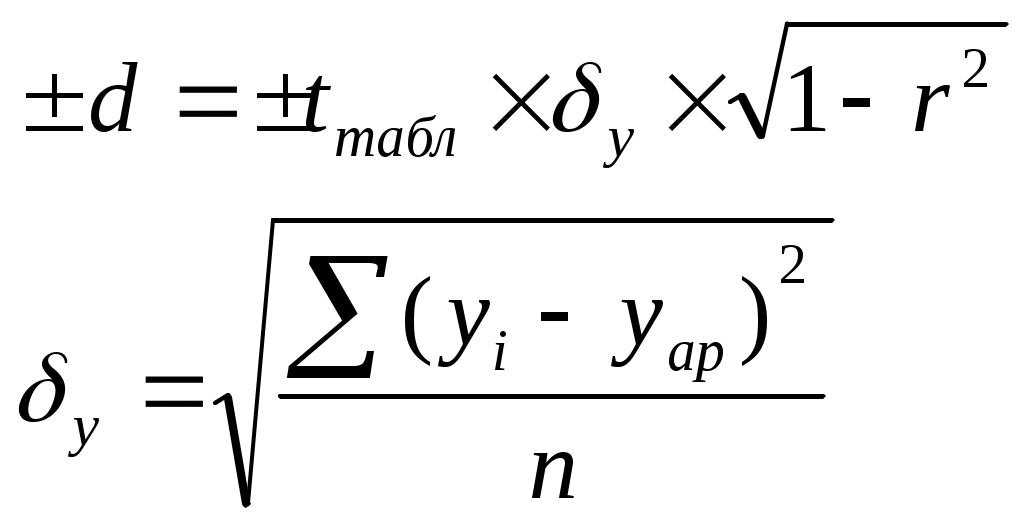 (7.6.) (7.6.)
(7.7)
Таблица 7.2 – Исходные и расчетные данные
Порядковый номер данных, i
|
Значение расходов по переделу (yi)
|
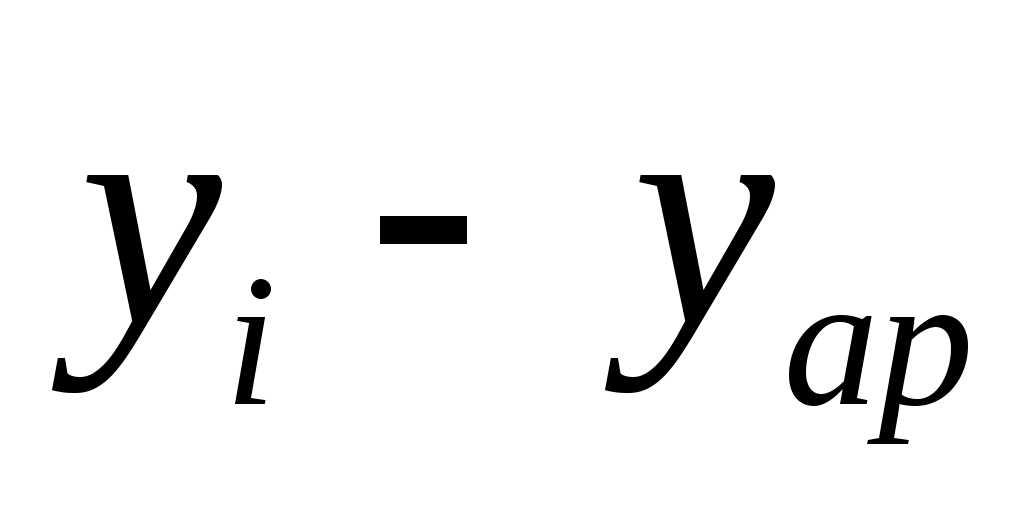
|
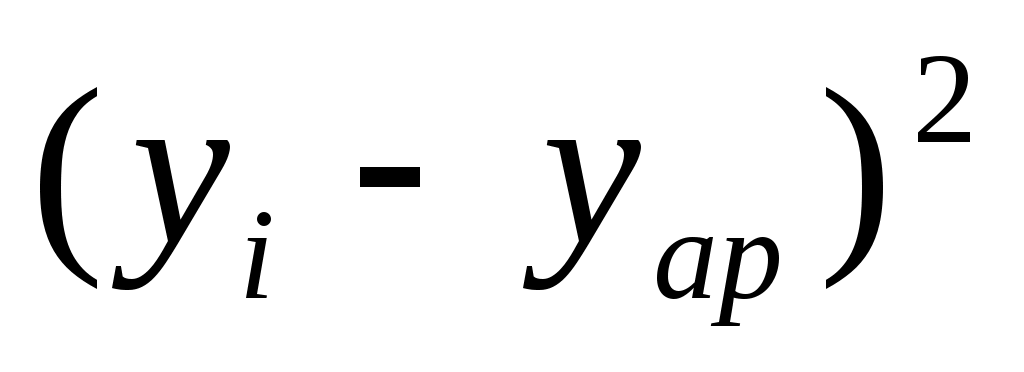
|
1
|
6
|
-3,78
|
14,288
|
2
|
7
|
-2,78
|
7,7284
|
3
|
7,1
|
-2,68
|
7,1824
|
4
|
7,5
|
-2,28
|
5,1984
|
5
|
8
|
-1,78
|
3,1684
|
6
|
8
|
-1,78
|
3,1684
|
7
|
8,5
|
-1,28
|
1,6384
|
8
|
9
|
-0,78
|
0,6084
|
9
|
9
|
-0,78
|
0,6084
|
10
|
10
|
0,22
|
0,0484
|
11
|
9,5
|
-0,28
|
0,0784
|
12
|
10
|
0,22
|
0,0484
|
13
|
10,6
|
0,82
|
0,6724
|
14
|
10
|
0,22
|
0,0484
|
15
|
11
|
1,22
|
1,4884
|
16
|
11
|
1,22
|
1,4884
|
17
|
9,2
|
-0,58
|
0,3364
|
18
|
11
|
1,22
|
1,4884
|
19
|
9,2
|
-0,58
|
0,3364
|
20
|
10
|
0,22
|
0,0484
|
21
|
10
|
0,22
|
0,0484
|
22
|
10,4
|
0,62
|
0,3844
|
23
|
10,6
|
0,82
|
0,6724
|
24
|
10,5
|
0,72
|
0,5184
|
25
|
11
|
1,22
|
1,4884
|
26
|
11
|
1,22
|
1,4884
|
27
|
11,5
|
1,72
|
2,9584
|
28
|
11,9
|
2,12
|
4,4944
|
29
|
11,8
|
2,02
|
4,0804
|
30
|
13
|
3,22
|
10,368
|
Итого
|
293,3
|
|
76,174
|
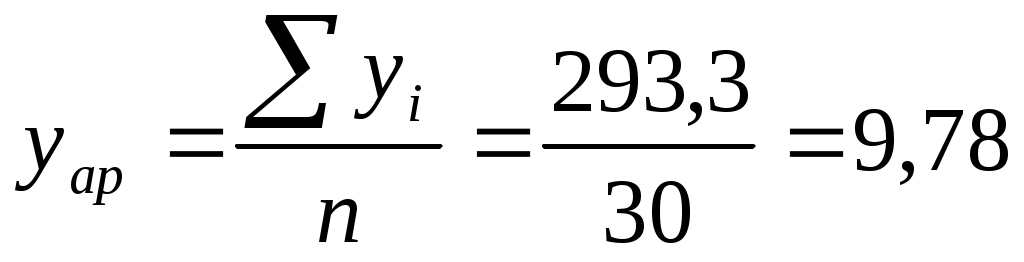 тыс.т. тыс.т.
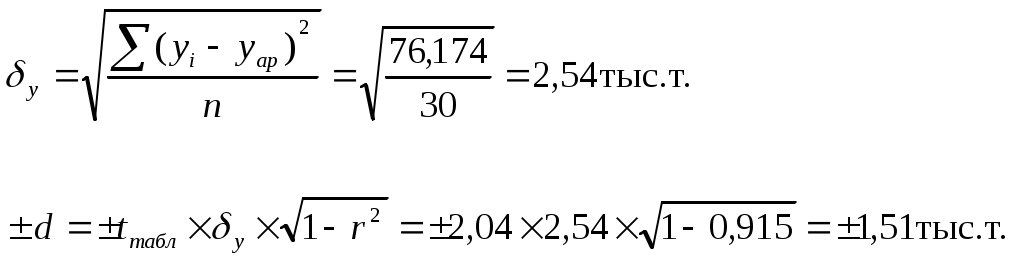
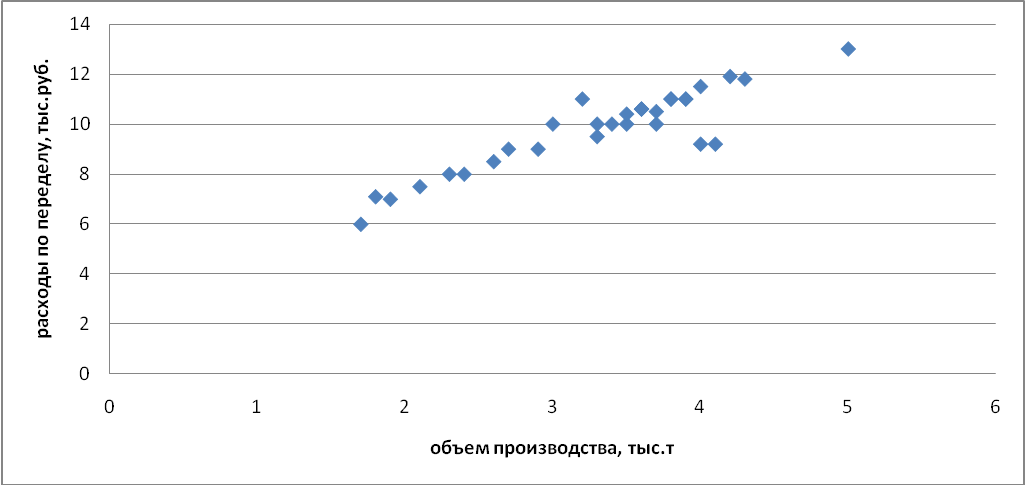
Рис. 7.5. Поле корреляции, теоретическая линия и ее доверительные интервалы
8) Сделать оценку предсказательной силы модели по остаточной дисперсии:
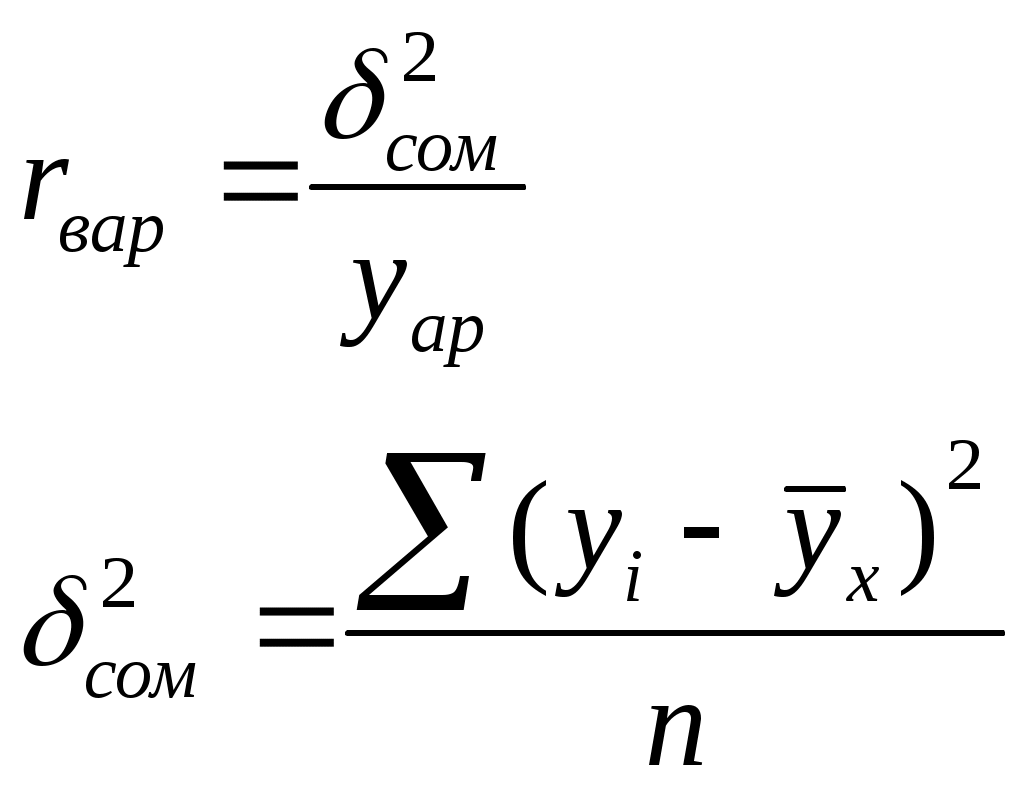
(7.8)
(7.9)
Таблица 7.3 – Исходные и расчетные данные
Порядковый номер данных, i
|
Объем производства, тыс.т. (xi)
|
Значение расходов по переделу (yi)
|
Значение линейной функции, y(x)
|
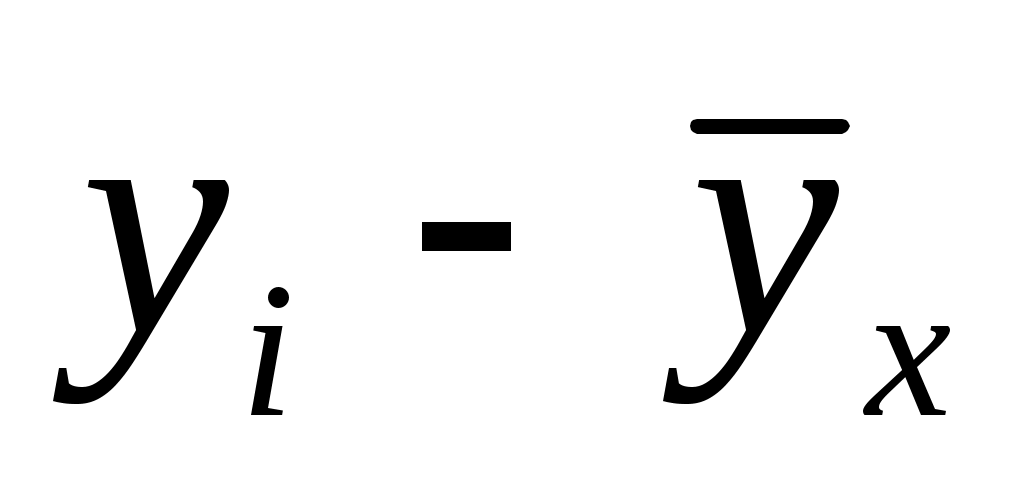
|
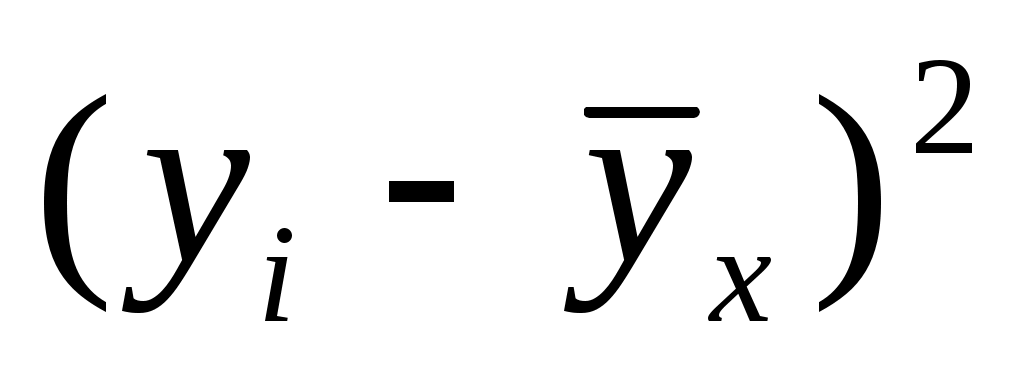
|
1
|
1,7
|
6
|
6,854
|
-2,924
|
8,54978
|
2
|
1,9
|
7
|
7,218
|
-2,56
|
6,5536
|
3
|
1,8
|
7,1
|
7,036
|
-2,742
|
7,51856
|
4
|
2,1
|
7,5
|
7,582
|
-2,196
|
4,82242
|
5
|
2,3
|
8
|
7,946
|
-1,832
|
3,35622
|
6
|
2,4
|
8
|
8,128
|
-1,65
|
2,7225
|
7
|
2,6
|
8,5
|
8,492
|
-1,286
|
1,6538
|
8
|
2,7
|
9
|
8,674
|
-1,104
|
1,21882
|
9
|
2,9
|
9
|
9,038
|
-0,74
|
0,5476
|
10
|
3
|
10
|
9,22
|
-0,558
|
0,31136
|
11
|
3,3
|
9,5
|
9,766
|
-0,012
|
0,00014
|
12
|
3,5
|
10
|
10,13
|
0,352
|
0,1239
|
13
|
3,6
|
10,6
|
10,312
|
0,534
|
0,28516
|
14
|
3,7
|
10
|
10,494
|
0,716
|
0,51266
|
15
|
3,8
|
11
|
10,676
|
0,898
|
0,8064
|
16
|
3,9
|
11
|
10,858
|
1,08
|
1,1664
|
17
|
4
|
9,2
|
11,04
|
1,262
|
1,59264
|
18
|
3,2
|
11
|
9,584
|
-0,194
|
0,03764
|
19
|
4,1
|
9,2
|
11,222
|
1,444
|
2,08514
|
20
|
3,3
|
10
|
9,766
|
-0,012
|
0,00014
|
21
|
3,4
|
10
|
9,948
|
0,17
|
0,0289
|
22
|
3,5
|
10,4
|
10,13
|
0,352
|
0,1239
|
23
|
3,6
|
10,6
|
10,312
|
0,534
|
0,28516
|
24
|
3,7
|
10,5
|
10,494
|
0,716
|
0,51266
|
25
|
3,8
|
11
|
10,676
|
0,898
|
0,8064
|
26
|
3,9
|
11
|
10,858
|
1,08
|
1,1664
|
27
|
4
|
11,5
|
11,04
|
1,262
|
1,59264
|
28
|
4,2
|
11,9
|
11,404
|
1,626
|
2,64388
|
29
|
4,3
|
11,8
|
11,586
|
1,808
|
3,26886
|
30
|
5
|
13
|
12,86
|
3,082
|
9,49872
|
Итого
|
99,2
|
293,3
|
293,34
|
-
|
63,7924
|
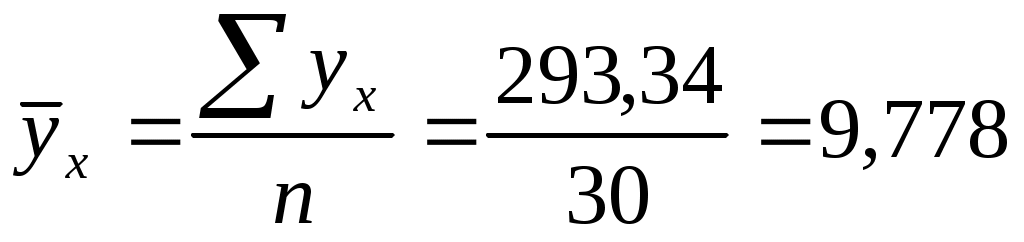 тыс.т. тыс.т.
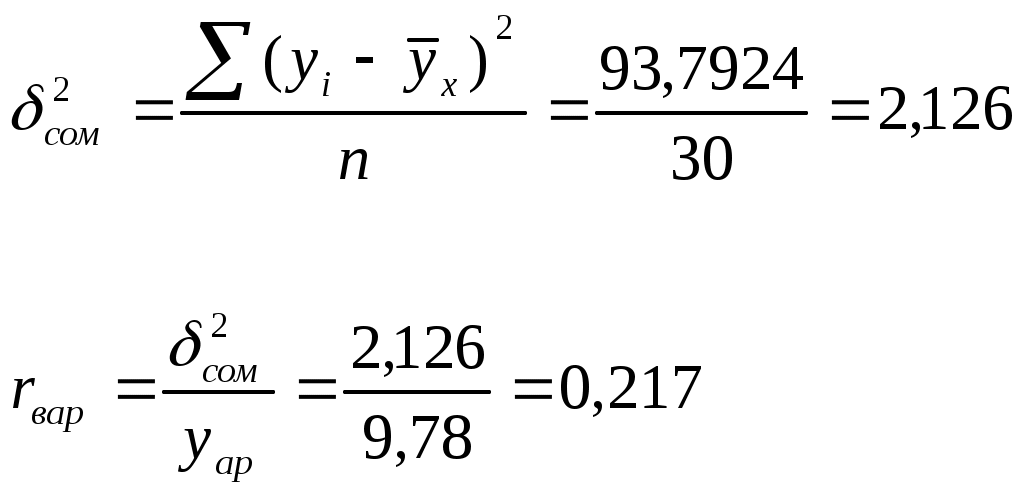 тыс.т. тыс.т.
Задача 8. По данным таблицы 2.9 рассчитать:
Индивидуальные индексы:
цен (по каждому предприятию);
физического объема (по каждому предприятию и средний по группе предприятий).
Сделать выводы.
Агрегатные индексы цен:
с постоянными весами;
с переменными весами;
структурных сдвигов.
Определить общее абсолютное изменение выручки от реализации товаров, а также изменение за счет цен и изменение за счет объема товаров в натуральном измерении. Сделать проверку результирующего влияния факторов.
По каждому индексу сделать обстоятельный вывод.
Построить график, отражающий результаты факторного анализа
Таблица 2.9 – Объем и цены реализованных товаров
Цены, руб.
|
Объем товаров, тыс. шт.
|
1 предприятие
|
2 предприятие
|
1 предприятие
|
2 предприятие
|
2004
|
2005
|
2004
|
2005
|
2004
|
2005
|
2004
|
2005
|
105
|
130
|
100
|
140
|
3,0
|
3,3
|
3,5
|
3,3
|
|
 Скачать 1.25 Mb.
Скачать 1.25 Mb.

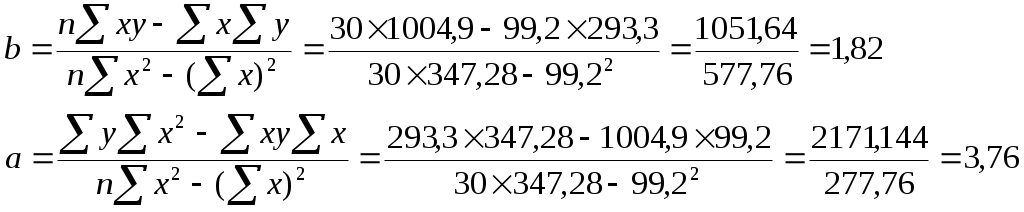 (7.3)
(7.3)
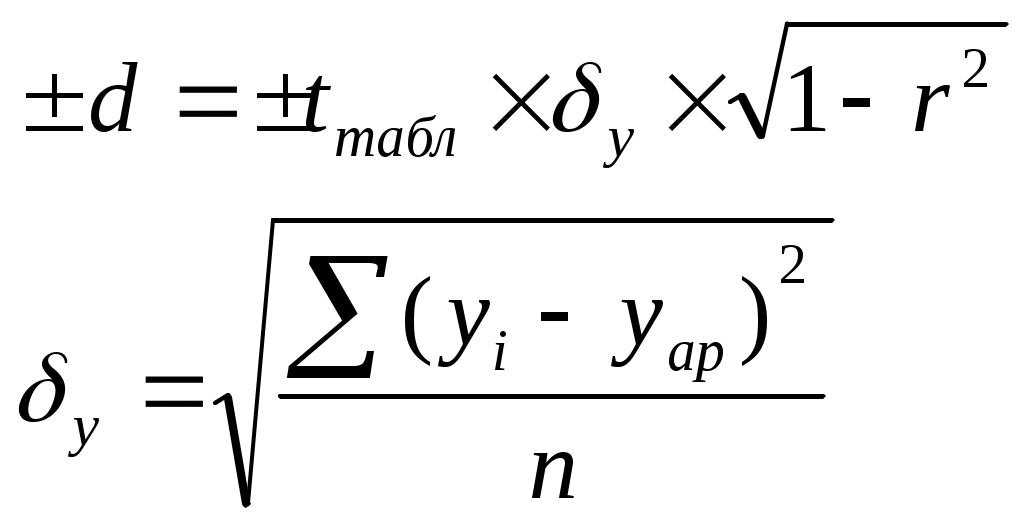 (7.6.)
(7.6.)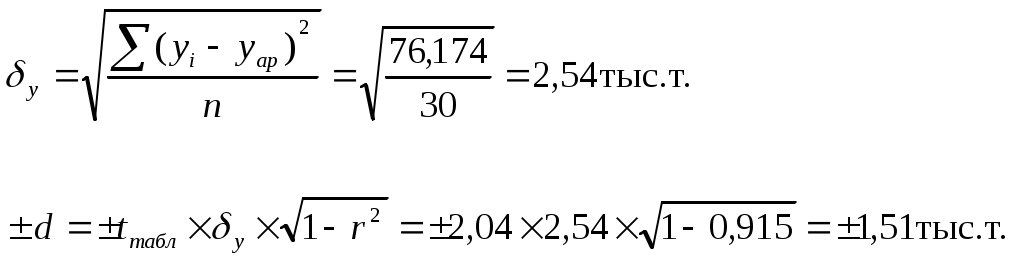

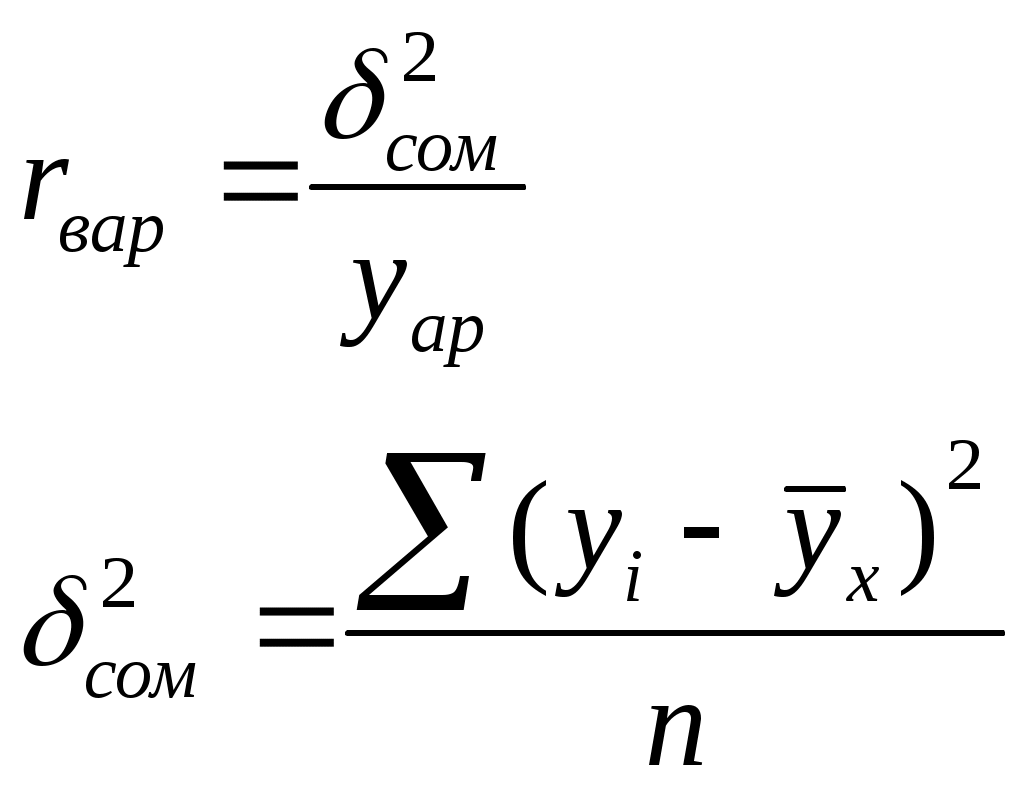
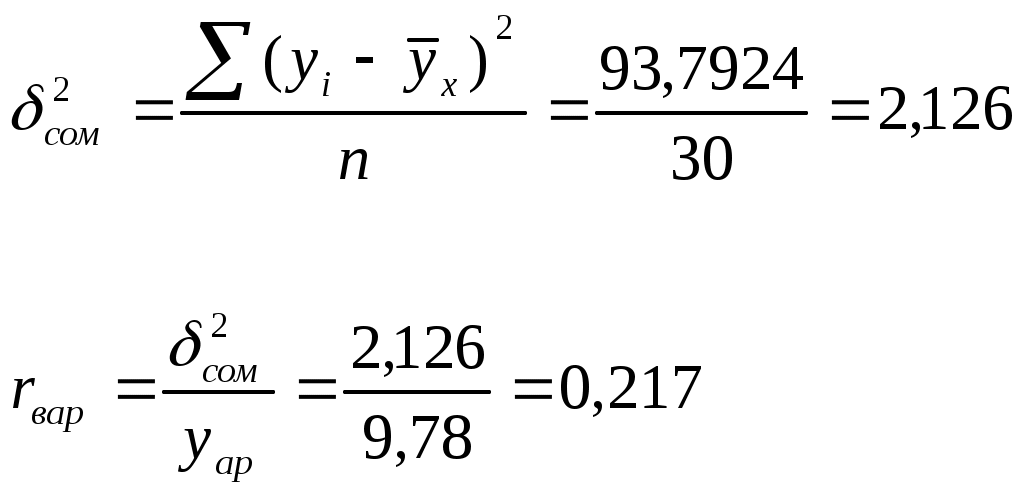 тыс.т.
тыс.т.