Контрольная по статистике. Статистика 2 вариант исправленный. Средние показать на графике, сделать выводы
 Скачать 1.25 Mb.
|
|
Решение Рассчитать индивидуальные индексы цен (по каждому предприятию), физического объема (по каждому предприятию и средний по группе предприятий).
Цена на продукцию первого предприятия возросла на 23,8%, на продукцию второго предприятия - на 40 %. Объем произведенных товаров на первом предприятии возрос на 10 %, а на втором снизился на 5,7%. Средний индекс физического объема по группе предприятий:  (101,729%) (8.1)В среднем, объем реализованной продукции возрос на 1,729%. Рассчитать агрегатные индексы цен. Общий индекс цен в агрегатной форме Общий индекс цен переменными весами:  (133,98%) (8.2)Цены по двум предприятиям возросли в среднем на 33,98%. Общий индекс цен с постоянными весами:  (131,71%) (8.3)Цены по двум предприятиям возросли на 31,71 % за счет изменения индивидуальных цен на каждом предприятии. Постоянный вес позволяет исключить влияние изменения структуры совокупности на величину индекса цен. Индекс структурных сдвигов:  (101,73%) (8.4)Индекс структурных сдвигов характеризует влияние изменения структуры товаров на динамику цен. За счет изменения удельного веса проданной продукции каждого предприятия в общем объеме продаж, цены возросли на 7,29% Взаимосвязь индексов: Iпер.в. = Iпост.в. × Iструктур.сдв. 1,3398 = 1,3171×1,0173 Общее абсолютное изменение выручки:  (8.5)Таким образом, выручка возросла на 226 тыс. руб. Изменение выручки за счет изменения цен:  (8.6)За счет роста цен, выручка увеличилась на 214,5 тыс.руб. Изменение выручки за счет изменения объема товаров в натуральном измерении:  (8.7)За счет изменения структуры реализованных товаров в натуральном выражении, выручка увеличилась на 11,5 тыс. руб. Таким образом, факторы, влияющие на выручку, действовали однонаправлено. Проверка: 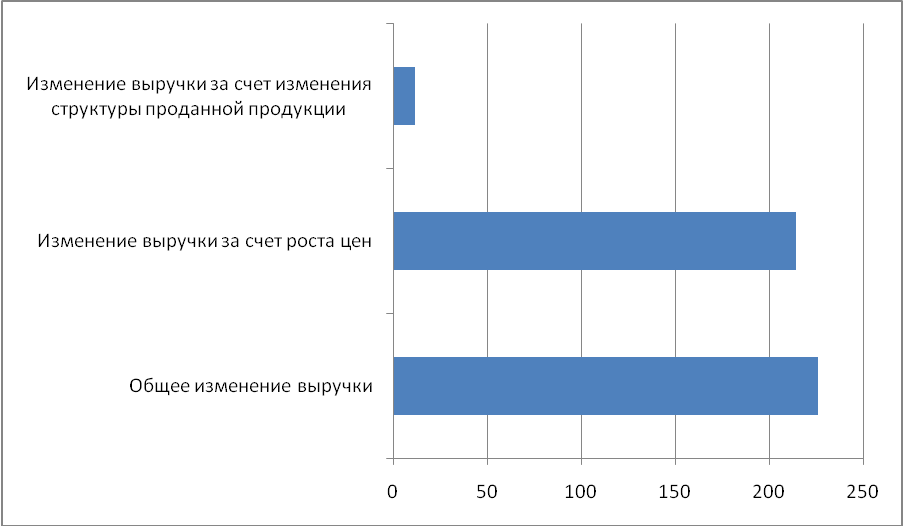  Рис. 8.1. Факторный анализ выручки Задача 9. Написать формулу темпа инфляции и объяснить ее. Рассчитать темп инфляции, сформировав потребительскую корзину из десяти наименований продуктов, товаров и услуг по своему усмотрению. Базовые и текущие цены, нормы потребления принять самостоятельно. Сделать вывод об уровне инфляции. Решение Инфляция измеряется с помощью индекса цен. Существуют различные методы расчета данного индекса: индекс потребительских цен, индекс цен производителей, индекс-дефлятор ВВП. Эти индексы различаются составом благ, входящих в оцениваемый набор, или корзину. Для того чтобы рассчитать индекс цен, необходимо знать стоимость рыночной корзины в данном (текущем) году и ее же стоимость в базовом году (году, принятом за точку отсчета). Общая формула индекса цен выглядит следующим образом:  (9.1)Предположим, что за базовый принят 2010 г. В этом случае необходимо рассчитать стоимость рыночного набора в текущих ценах, т.е. в ценах данного года (числитель формулы) и стоимость рыночного набора в базовых ценах, т.е. в ценах 2010 г. (знаменатель формулы). Поскольку уровень (или темп) инфляции показывает, на сколько процентов цены выросли за год, то его можно рассчитать следующим образом:  (9.2)ИЦ0 — индекс цен предыдущего года (например, 2011), ИЦ1 — индекс цен текущего года (например, 2012). Таблица 9.1 – Характеристика потребительской корзины
Рассчитаем индекс цен в 2011 и 2012 гг. 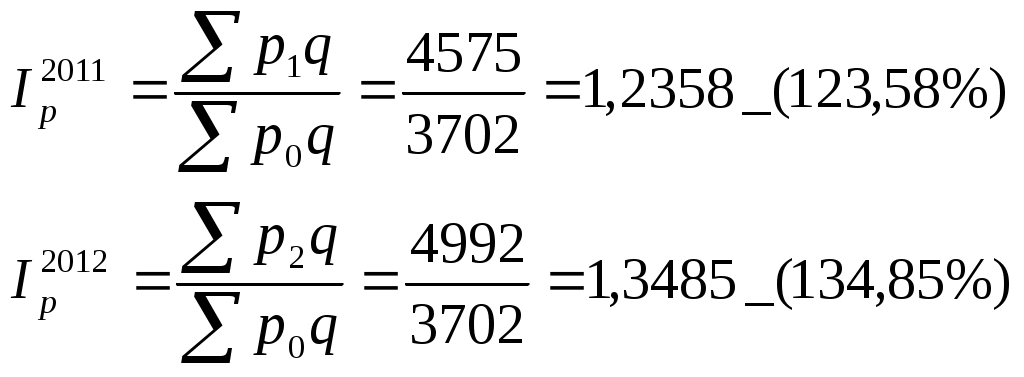 (9.3)(9.4) Т.е. цены на потребительскую корзину выросли на 23,58% в 2011 г. по сравнению с базисным годом, и на 34,85% в 2012 г. по сравнению с базисным годом. Определим темп инфляции в 2012г. на основе уже рассчитанных данных: 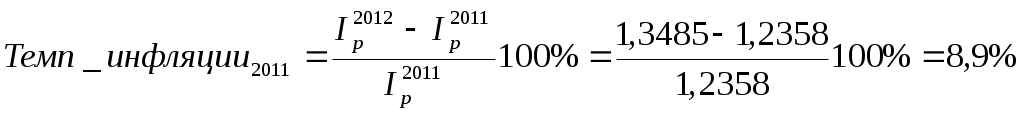 Цены на потребительскую корзину в 2011г. выросли по сравнению с 2010г. на 8,9%. Задача 10. По данным таблицы 2.10 рассчитать характеристики генеральной и выборочной совокупностей, а также ошибки при исчислении средней и доли в случаях повторного и бесповторного отборов. Выборка 40%. Частоты в выборочной совокупности принять произвольно. Уровень вероятности равен 0,954, коэффициент Стьюдента – 2. Таблица 2.10 – Исходные данные
Решение Исходные и расчетные данные сгруппируем в таблицу. Частоты в выборочной совокупности по условию задачи принимаем произвольно. Таблица 10.1 – Генеральная и выборочная совокупности
Рассчитаем характеристики генеральной средней Таблица 10.2 – Характеристика генеральной совокупности
где М – число единиц совокупности, чьи значения превышают среднее значение признака в совокупности; N – число элементов в совокупности. В совокупности 31 элемент, чье значение (5, 6, 7, 8) превышает средний уровень, равный 4,1. Таким образом, в генеральной совокупности 44% единиц обладают значениями признака, превышающими средний уровень, 56% - обладают значениями признака меньшими, чем средний уровень. Рассчитаем характеристики выборочной средней | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
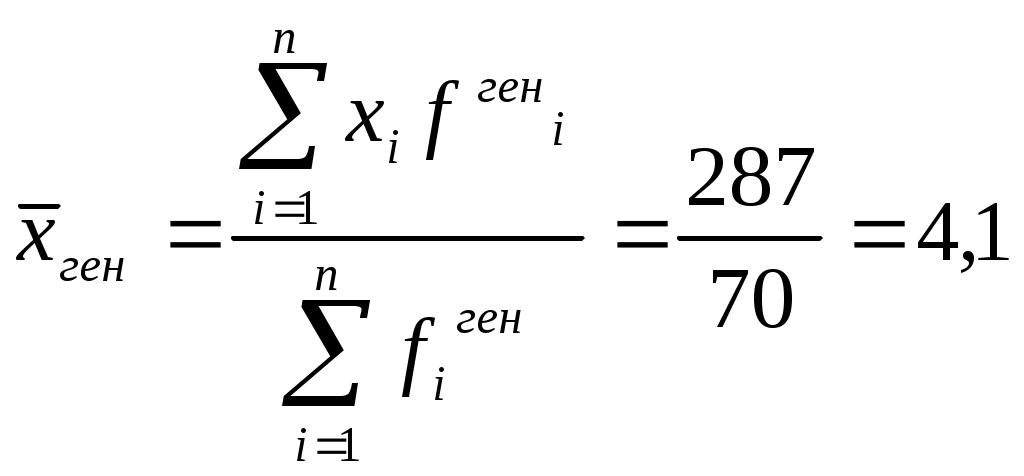(10.1)
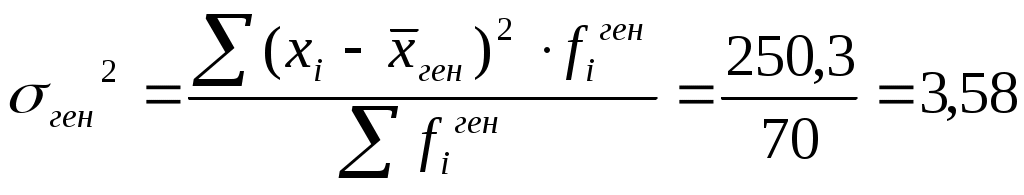(10.2)
, (10.3)
(10.4)