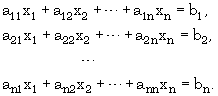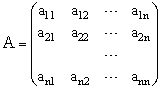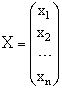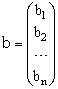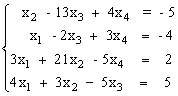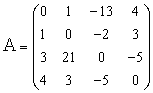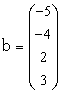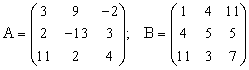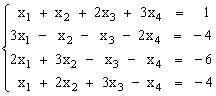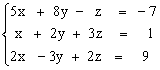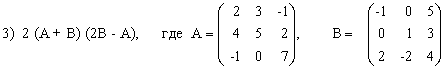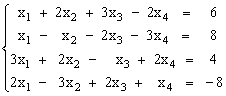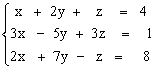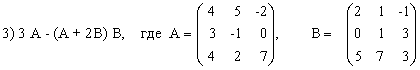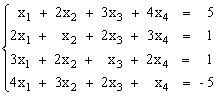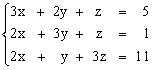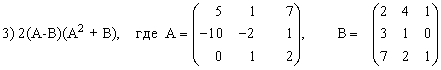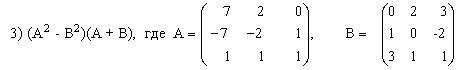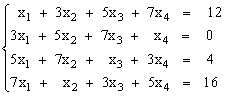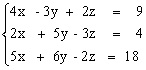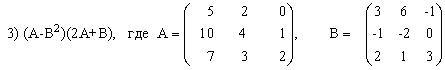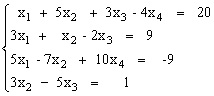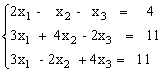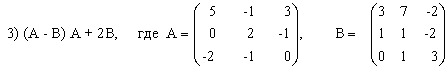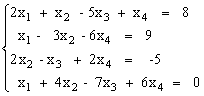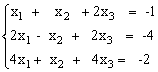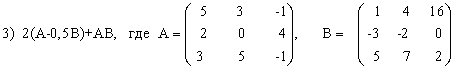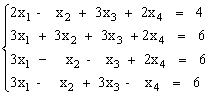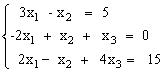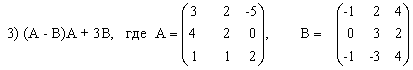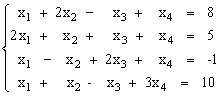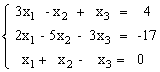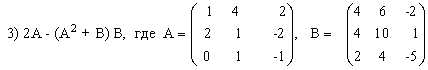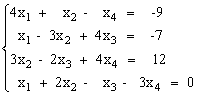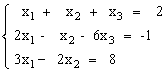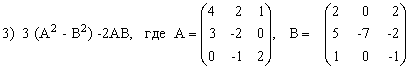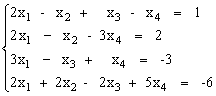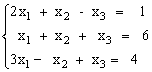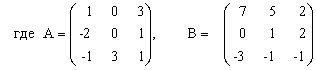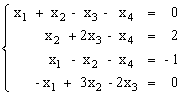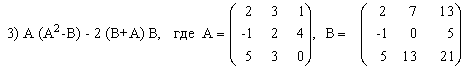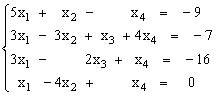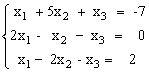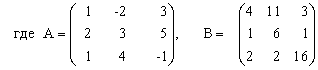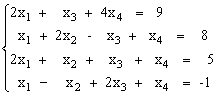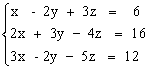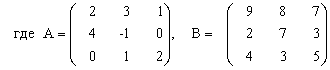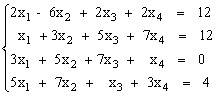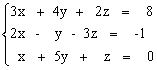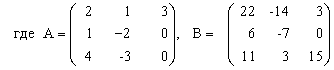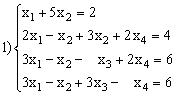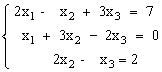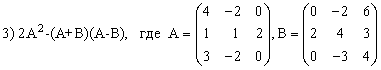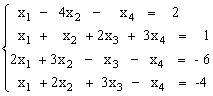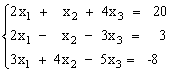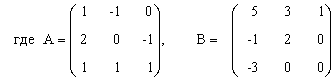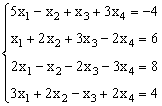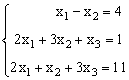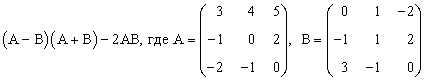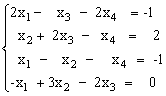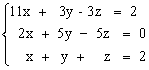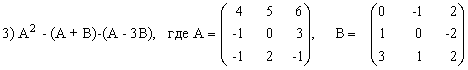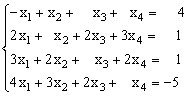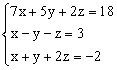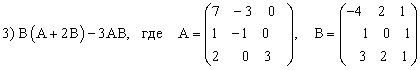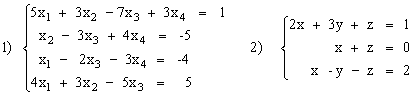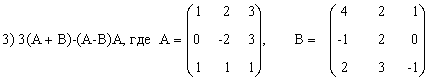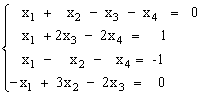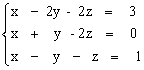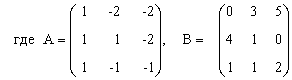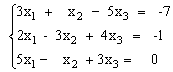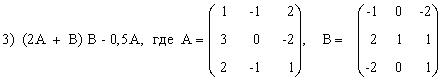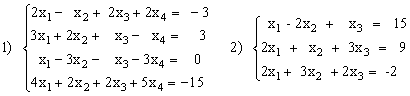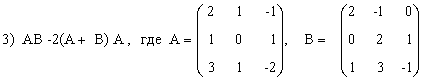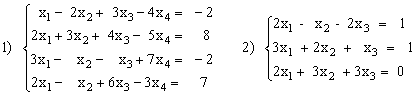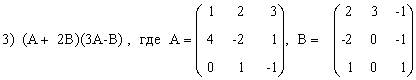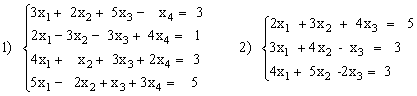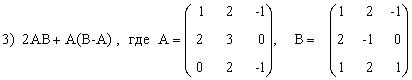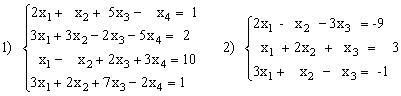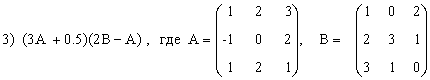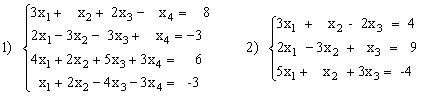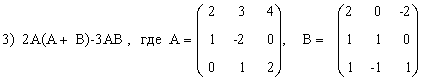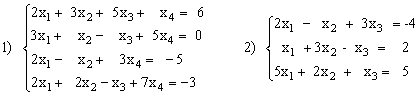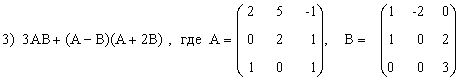Лабораторная работа № 5. Численные методы решения систем уравнений.
Цель работы: Изучение возможностей пакета Ms Excel при решении задач линейной алгебры. Приобретение навыков решения систем линейных алгебраических уравнений и выполнение действий над матрицами средствами пакета.
Задание: решить систему уравнений методом Гаусса, методом LU-разложения, методом Зейделя
Решение систем линейных алгебраических уравнений (СЛАУ)
Пусть задана СЛАУ следующего вида:
Эту систему можно представить в матричном виде: AX = b, где
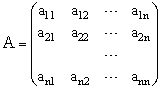
|
- матрица коэффициентов системы уравнений;
|
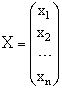
|
- вектор неизвестных,
|
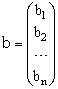
|
- вектор правых частей.
|
При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.
Метод обратной матрицы
Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
A-1AX=A-1b, EX=A-1b, (E - единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле X=A-1b.
Метод Крамера
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
где
|
|
- определитель матрицы A,
|
|
- определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
|
|
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на следующих примерах.
ПРИМЕР 3.1. Решить систему методом обратной матрицы:
В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:
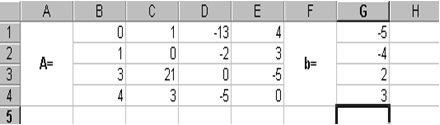
Введём матрицу A и вектор b в рабочий лист MS Excel (рис. 3.1).
|
Рис. 3.1
|
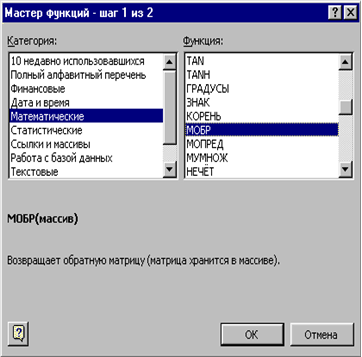
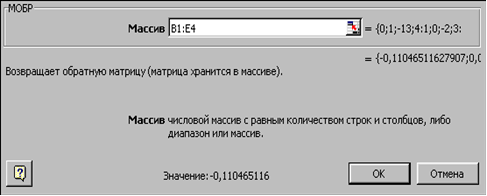
В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно!!!); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы (рис. 3.2), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 3.3). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица - в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
|
Рис. 3.2
|
|
Рис. 3.3
|
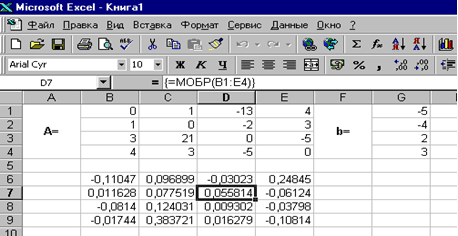
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид изображенный на рис. 3.4.
|
Рис. 3.4
|
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА
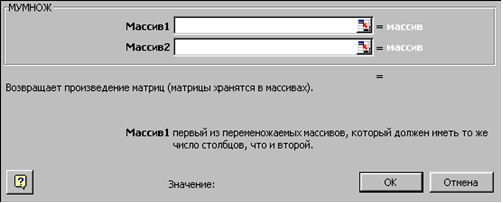
Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 3.5) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b).
|
Рис. 3.5
|
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор х), находится в ячейках H6:H9.
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x и получить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(В1:Е4;Н6:Н9), так как было описанной выше.
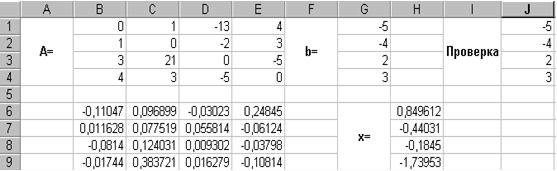
В результате проведенных вычислений рабочий лист примет вид изображенный на рис. 3.6.
|
Рис. 3.6
|
ПРИМЕР 3.2. Решить систему из ПРИМЕРА 3.1 методом Крамера.
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 3.7).
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
I11=МОПРЕД(B6:E9), I12=МОПРЕД(B11:E14),
I13=МОПРЕД(B16:E19), I14=МОПРЕД(B21:E24).
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 - вспомогательные.
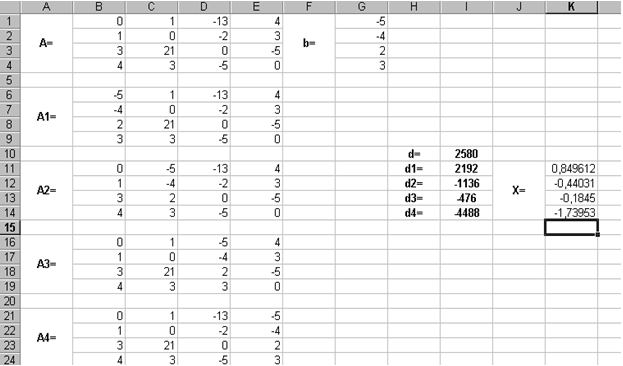
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
|
Рис. 3.7
|
ПРИМЕР 3.3. Вычислить матрицу С по формуле: C=A2+2AB, где
Введем исходные данные на рабочий лист (рис. 3.8).
Для умножения матрицы А на матрицу В, выделим диапазон B5:D7 и воспользуемся функцией МУМНОЖ(B1:D3;G1:I3).
Результат вычисления A2=A*A поместим в ячейки G5:I7, воспользовавшись формулой МУМНОЖ(B1:D3;B1:D3).
Умножение (деление) матрицы на число можно выполнить при помощи элементарных операций. В нашем случае необходимо умножить матрицу из диапазона B5:D7 на число 2. Выделим ячейки B9:D11 и введем формулу =2*B5:D7.
Сложение (вычитание) матриц выполняется аналогично. Например, выделим диапазон G9:I11 и введем формул =B9:D11+ G5:I7.
Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
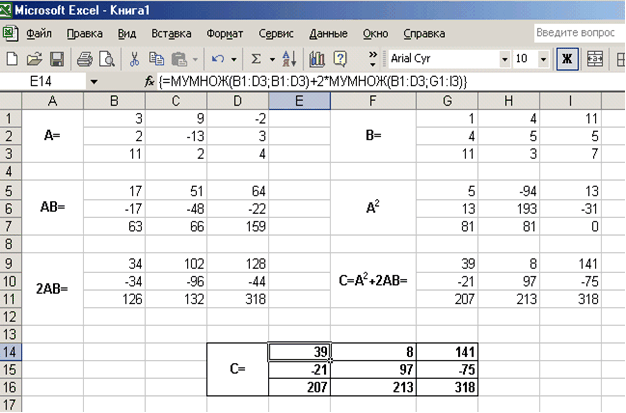
Кроме того, в строке формул рабочего листа, изображенного на рис. 3.8, показано как можно вычислить матрицу С одним выражением.
|
Рис. 3.8
|
ВАРИАНТЫ ЗАДАНИЙ
Решить систему уравнений методом Крамера.
Решить систему уравнений с помощью обратной матрицы.
Выполнить действия над матрицами.
При решении систем обязательно выполнить проверку.
Вариант №11
|
1)
|
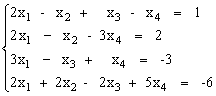
|
2)
|
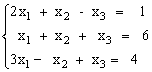
|
|
|
|
|
|
3) (2A-B)(3А+B)-2АВ,
|
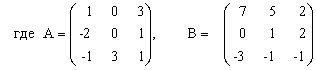
|
|
|
Вариант №13
|
1)
|
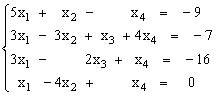
|
2)
|
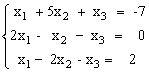
|
|
|
|
|
|
3) (A+B)A-B(2А+3В),
|
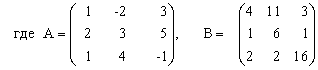
|
|
|
Вариант №14
|
1)
|
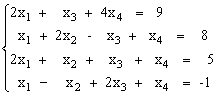
|
2)
|
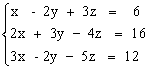
|
|
|
|
|
|
3) A(2A+B)-B(А-В),
|
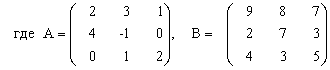
|
|
|
Вариант №15
|
1)
|
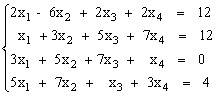
|
2)
|
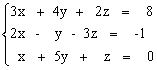
|
|
|
|
|
|
3) 3(A+B)(AВ-2А),
|
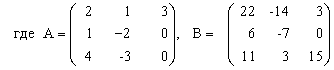
|
|
|
Вариант №17
|
1)
|
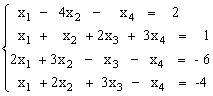
|
2)
|
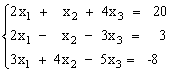
|
|
|
|
|
|
3) 2А + 3B(АB-2А),
|
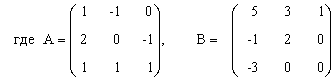
|
|
|
Вариант №19
|
1)
|
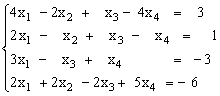
|
2)
|
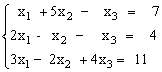
|
|
|
|
|
|
3) 2A - АB(В - А) + В,
|
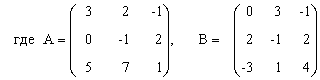
|
|
|
Вариант №22
|
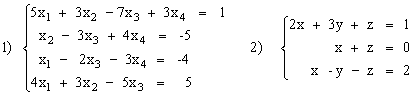
|
|
|
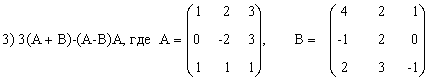
|
Вариант №23
|
1)
|
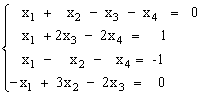
|
2)
|
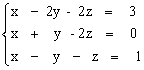
|
|
|
|
|
|
3) А(A - B) + 2В(A + В),
|
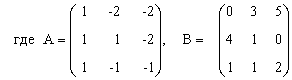
|
|
|
Вариант №25
|
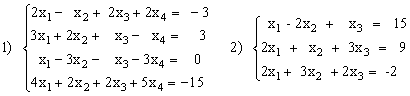
|
|
|
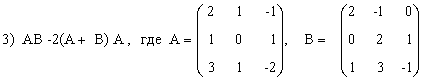
|
Вариант №26
|
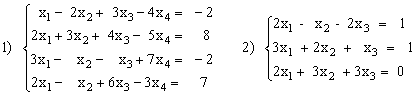
|
|
|
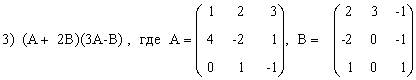
|
Вариант №27
|
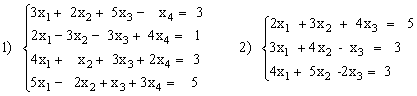
|
|
|
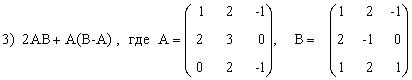
|
Вариант №28
|
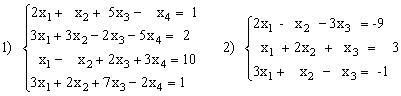
|
|
|
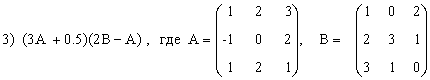
|
Вариант №29
|
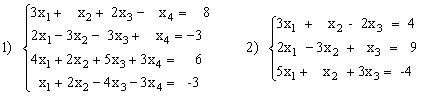
|
|
|
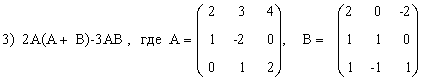
|
Вариант №30
|
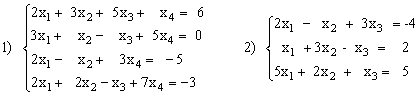
|
|
|
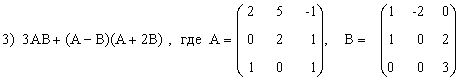
|
|
 Скачать 0.93 Mb.
Скачать 0.93 Mb.