симплекс метод. Лабораторная работа 3 Решение однокритериальных задач принятия решений методами линейного программирования Общие сведения

Название	Лабораторная работа 3 Решение однокритериальных задач принятия решений методами линейного программирования Общие сведения
Анкор	симплекс метод
Дата	14.10.2021
Размер	1.31 Mb.
Формат файла
Имя файла	Laboratornaya_rabota_3.docx
Тип	Лабораторная работа #247388
страница	4 из 5

1 2 3 4 5

Анализ математического решения проблемы и формирование управленческого решения

На этом этапе требуется на основе полученного с использованием «Поиска решений» решения математической модели найти решение реальной проблемы. В процессе построения модели были сделаны различные допущения, упрощающие реальную ситуацию, в результате чего появилась возможность формализовать модель. Зависимости, зафиксированные в модели, лишь приближенно отображают реальные зависимости между факторами и переменными решения и объективной целью. Знания факторов, влияющих на цель, являются неполными, а значения факторов — приближенные. В соответствие с последним встаёт вопрос: если реальные значения параметров отличаются от тех, которые заложены в модели, то изменится ли решение, и если да, то на сколько изменится?

На подобные вопросы призван дать ответ анализ полученного решения, корректно называемый анализом чувствительности решения. Анализ чувствительности проводится после получения оптимального решения математической модели и дает информацию, которую нужно использовать при принятии решения в реальной ситуации.

Анализ чувствительности позволяет ответить на следующие вопросы:

В каких пределах могут изменяться параметры модели так, чтобы сохранилось полученное решение?
Какие ограничения связанные (т.е. влияют на целевую функцию), а какие ограничения не влияют на решение?
Если изменить значения правых частей связанных ограничений, то насколько может измениться значение целевой функции?
Если значение какой-то переменной решения равно нулю, то при каких условиях она может принять положительное значение? (Вопрос весьма актуален для моделей производства.)

Знакомство с отчётами

Средство «Поиск решения» может генерировать три вида отчетов: «Результаты» (см. Рисунок 11), «Устойчивость» (см. Рисунок 12) и «Пределы» (см. Рисунок 13). Перечисленные виды отчётов по своей форме специфичны, «Поиск решения» создает их только для линейных моделей. Для прочих методов решения задач состав отчётов может быть иным или отчёты могут иметь другой вид. Рассмотрим применение отчетов для выполнения анализа чувствительности линейных моделей.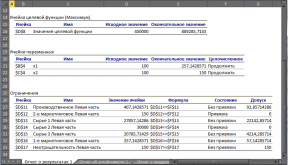

Рисунок 11. Отчет о результатах

Рисунок 12. Отчёт об устойчивости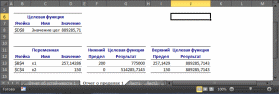

Рисунок 13. Отчёт о пределах
Отчет по результатам полезен для анализа чувствительности тем, что там явно указано, какие ограничения связанные и какие несвязанные. Эти данные приведены в отчете в таблице «Ограничения» в столбце «Состояние». В столбце «Допуск» той же таблицы показаны значения разностей между левыми и правыми частями ограничений.

Отчет об устойчивости в целях анализа чувствительности представляет большую пользу. В таблице «Ячейки переменных» этого отчета приведена информация о значениях изменяемых ячеек:

Ячейка – адрес ячейки переменной;
Имя. Создаётся заранее или составляется из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки. Если имен нет, то это поле остается пустым;
Окончательное значение – значение переменной, найденное средством «Поиск решения»;
Приведённая стоимость – показывает, как изменится оптимальное значение целевой функции при выпуске продукции, которой нет в оптимальном плане. В рассматриваемом примере оптимальный план предполагает выпуск обоих типов дисплеев, поэтому их приведённая стоимость равна нулю. Если бы оптимальное значение какой-либо из неизвестных было равно нулю (xi = 0), а приведённая стоимость равнялась бы, например, –3, то принудительный выпуск 2-х единиц этой переменной xi (т. е. добавление нового ограничения xi ≥ 2) привел бы к изменению (уменьшению) целевой функции на 2*(–3) = –6 единиц. Необходимо отметить, что из равенства нулю оптимального значения неизвестной не следует априорно, что ее приведённая стоимость будет отлична от нуля;
Целевая функция Коэффициент – коэффициент, стоящий при данной изменяемой переменной в формуле целевой функции;
Допустимое увеличение и Допустимое уменьшение – показывают, в каких пределах может изменяться целевой коэффициент при условии, что найденные значения переменных останутся неизменными.

В таблице «Ограничения» соответственно названию приведена информация об ограничениях:

Ячейка – адрес ячейки, на значение которой наложено ограничение;
Имя. Создаётся заранее или составляется из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки. Если имен нет, то это поле остается пустым;
Окончательное значение – значение в ячейке, найденное средством «Поиск решения»;
Тень Цена – показывает, насколько изменится значение целевой функции, если на единицу изменится значение правой части данного ограничения; теневая цена отлична от нуля только тогда, когда данное ограничение в оптимальном решении является связанным;
Ограничение Правая сторона – значение правой части ограничения;
Допустимое увеличение и Допустимое уменьшение – показывают пределы изменения правой части ограничения, в которых действует приведенное значение теневой цены («Тень Цена») данного ограничения¹.

Наиболее важными данными для анализа чувствительности в этом отчете являются нормированные стоимости и теневые цены, применение которых будет рассмотрено ниже. Важно отметить, что значения теневых цен подсчитаны в предположении, что изменяется значение правой части только одного ограничения при условии постоянства всех остальных параметров модели.

В отчете по пределам в столбцах Нижний предел и Верхний предел показано, в каких пределах с учетом всех ограничений могут изменяться переменные и какие при этом значения будет принимать целевая функция (значения в столбцах «Целевая функция Результат»). Стоит отметить, что если на значения переменной не налагаются явные ограничения, задающие ее верхнюю или нижнюю границу, то в столбцах «Верхний предел»/«Нижний предел» и «Целевой результат» для этой переменной будут стоять значения ошибки «#Н/Д».

Анализ привязки решения к ограничениям

Приступим к анализу чувствительности в рассматриваемом примере. Во-первых, требуется заметить, что переменные решения нулевые значения не принимают, что облегчает анализ. Рассмотрим ограничения. Первое ограничение, задающее предельный объем производства, связанным не является. Отсюда следует очевидный вывод о том, что такой производственный план задействует не все мощности завода. Это является серьёзным недостатком данного плана.

Рассмотрим, что сдерживает объемы производства. Связанными являются второе маркетинговое ограничение и ограничение по сырью 2 (на это указывает отчет о результатах и ненулевые значения теневых цен для этих ограничений в отчете по устойчивости). Влиять на маркетинговое ограничение трудно, поскольку требования отдела маркетинга формируются конъюнктурой рынка, но всё же они могут подвергаться изменению, для чего отдел маркетинга применяет собственные технологии для изменения конъюнктуры рынка, например рекламу и т.п. Однако в рассматриваемом примере особого смысла изменение маркетингового требования не имеет, т.к. чтобы полностью загрузить мощности производства, надо запланировать еще около 93 единиц продукции, а на такое увеличение производства за счёт маркетинга рассчитывать сложно, так как даже объем в 150 единиц трудно продать.

Другое лимитирующее ограничение определяется наличием на складе запаса сырья 2. Взглянем на теневую цену этого ограничения, она равна 28,57. Это означает, что изменение на одну единицу величины правой части данного ограничения (т.е. изменение величины запаса сырья 2 на 1 ед.) приведет к изменению на 28,57 руб. величины прибыли (значения целевой функции). Очевидно, что в данном случае при увеличении значения правой части ограничения значение целевой функции будет возрастать, а при уменьшении — убывать. Насколько же нужно увеличить запас сырья 2, чтобы полностью загрузить все производственные мощности? К сожалению, отчет по устойчивости прямого ответа на этот вопрос не дает.

Посмотрим на число в столбце Допустимое увеличение для этого ограничения. Оно равно 6500. Это значит, что, увеличивая значение правой части ограничения до величины 36500, мы остаемся в рамках прежнего решения — значения переменных и целевой функции, конечно, будут изменяться, но лимитирующими и нелимитирующими останутся прежние ограничения. Если же значение правой части ограничения будет равно или превысит величину 36500, то в качестве лимитирующего (привязка) выступит другое ограничение, которое на данный момент не является лимитирующим.

Чтобы узнать, что получится при изменении правой части пятого ограничения до величины 36500, необходимо опять запускать «Поиск решения». Внесите в ячейку F14 значение 36500 и выберите опять команду «Поиск решения». В диалоговом окне Поиск решения ничего менять не требуется, поскольку настройки были сохранены при предыдущем запуске. Нажмите на кнопку «Найти решение». После нахождения решения требуется выбрать все отчёты для повторного создания.

Новое решение отображает Рисунок 14. В новом решении х₁ = 350, х₂ = 150 и z = 1075000. Новым лимитирующим ограничением стало первое ограничение, задающее предельный объем производства. Рассматриваемый пример оказался «удачным» для аналитика, т.к. изменение только одного параметра модели (значения правой части ограничения по сырью 2) уже привело к решению (производственному плану), где производственные мощности завода задействованы полностью. В общем случае, если действительно есть необходимость задействовать все мощности производства, скорее всего, пришлось бы проверять другие лимитирующие ограничения и пробовать изменять их правые части.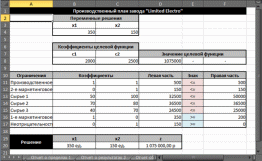

Рисунок 14. Новое оптимальное решение
На текущий момент анализа оптимальным производственным планом будет производство 350 ед. дисплеев типа 46” и 150 ед. дисплеев 51”. Однако, чтобы выполнить такой план, необходимо увеличить месячные запасы сырья 2 на 6500 единиц, а месячные запасы сырья 1 и сырья 3 можно уменьшить на 17500 и 500 ед. соответственно. Затем требуется подсчитать, на сколько увеличится (и увеличится ли) себестоимость продукции, если докупить дополнительные объемы сырья 2, так как возрастут расходы по крайней мере на хранение сырья. Это может повлиять на удельную прибыль дисплеев, т. е. могут измениться значения коэффициентов при переменных в формуле целевой функции. Если утверждения о увеличении цены продукции верны, то вычисления снова потребуется повторить. Кроме того, надо вспомнить, что значения этих коэффициентов (цены единицы) известны только приближенно. Поэтому далее следует рассмотреть влияние коэффициентов при переменных в формуле целевой функции.

Анализ коэффициентов целевой функции

Напомним, что в отчете по устойчивости коэффициенты целевой функции названы «Целевая функция Коэффициент», далее для краткости этот параметр будет называться просто коэффициент, и, как показывает Рисунок 14, этим коэффициентам с самого начала присвоены имена с1 и с2. В последнем отчете об устойчивости (см. Рисунок 15) в таблице «Ячейки переменных» в столбцах «Допустимое увеличение» и «Допустимое уменьшение» приведены значения, на которые могут изменяться целевые коэффициенты при условии сохранения решения. Сохранение решения здесь означает сохранение значений переменных решения, но значение целевой функции может изменяться. Однако следует учесть, что эти числа имеют смысл при выполнении дополнительного условия, а именно, что целевые коэффициенты изменяются по одному, а не совместно. Таким образом, на основании данных отчета по устойчивости можно утверждать, что если коэффициент с1 при переменной х1 будет изменяться в пределах от 0 до 2500 или коэффициент с2 при переменной х2 будет изменяться в пределах от 2000 до бесконечности, то значения этих переменных останутся прежними. На вопрос же каким будет решение, если изменятся оба целевых коэффициента, отчет по устойчивости ответа не дает. Этот ответ требуется получить самостоятельно.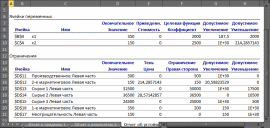

Рисунок 15. Отчет по устойчивости для решения с изменённым ограничением «Сырьё 2»
В примере целевой коэффициент с1 при переменной х1 может изменяться в пределах 1500 до 2300, а целевой коэффициент с2 при переменной х2 — в пределах от 2100 до 3000. Хотя эти пределы не перекрывают крайние значения, которые показаны в отчете об устойчивости, необходимо проверить решение при совместном изменении значений целевых коэффициентов. Для этого проверим граничные изменения коэффициентов, при этом важно учесть, что полученное решение, как показывает Рисунок 15, остаётся в силе пока целевой коэффициент с1, будет меньше целевого коэффициента с2. Поэтому в первую очередь требуется проверить решение, если коэффициент с1 будет равен 2300, а коэффициент с2 будет равен 2100. Запишите эти числа в ячейки В8 и С8 соответственно и запустите «Поиск решения», ничего не меняя в его установках, в результате будет получено новое решение (см. Рисунок 16).

Как можно было предположить, если удельная прибыль 51” дисплеев меньше удельной прибыли 46” дисплеев, то производить 51” дисплеи невыгодно. Отметим, что прибыль при данном решении больше, чем в предыдущем решении (1150000 руб. против 1075000 руб.), а сырья всех видов потребуется меньше, поскольку ни одно ограничение по сырью не является лимитирующим. И все-таки, если для поддержания ассортимента продукции необходимо производить дисплеи 51”, то насколько надо увеличить ее удельную прибыль, чтобы ее производство стало выгодным? Ответ здесь очевиден — надо как минимум сравнять удельные стоимости обоих типов краски. На это указывает число 200 в столбце «Допустимое увеличение» и в строке х2 таблицы «Ячейки переменных» отчета об устойчивости для данного решения (см. Рисунок 17).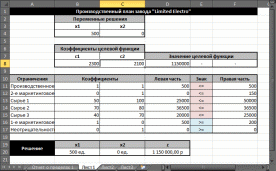

Рисунок 16. Решение при крайних значениях целевых коэффициентов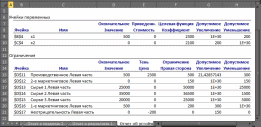

Рисунок 17. Отчет по устойчивости для решения при крайних значениях целевых коэффициентов
Если значения удельных прибылей сделать равными, то будет получен случай множественных альтернативных оптимальных решений задачи линейной оптимизации: любая пара неотрицательных чисел х1 и х2 таких, что x1 + x2 = 500 и х2  150, будет решением данной задачи, при этом значения целевой функции для любых таких решений будут одинаковыми. Чтобы убедиться в этом, введите в ячейки В8 и С8 одинаковые значения, например 2300. Запустите «Поиск решения». Будет получено новое решение х1 = 500 и х2 = 0 (см. Рисунок 18), поскольку это граничное решение, которое кроме прочего оптимизированно по ограничениям, т.е. в отчёте о результатах имеет наиболее оптимальные абсолютные значения допусков в таблице «Ограничения». Других решений в рассматриваемом примере, хотя их существует много, с использованием «Поиска решений» получено быть не может.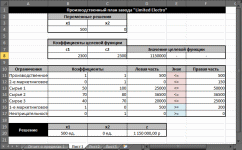

Рисунок 18. Решение предполагающее отказ от дисплеев 51”
В реальных задачах линейной оптимизации множественные оптимальные решения встречаются относительно редко. Более вероятно, эта ситуация может проявиться при проведении анализа чувствительности, как в последнем примере. Признак того, что при данном решении существуют другие альтернативные решения, дает отчет об устойчивости. Если в таблице «Ячейки переменных» в столбцах «Допустимое увеличение» и «Допустимое уменьшение» для некоторых переменных присутствуют нули, то это и является признаком того, что существуют альтернативные решения. Например, Рисунок 19 показывает отчет по устойчивости для рассматриваемой задачи, когда c1 = 2300 и c2 = 2300, а х1 = 500 и х2 = 0.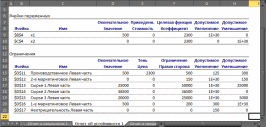

Рисунок 19. Отчет по устойчивости в случае множественных решений
Если некоторые переменные принимают нулевые значения, то еще одним признаком присутствия альтернативных решений будут нулевые значения нормированных стоимостей для этих переменных.

Наличие альтернативных решений делает необходимым выбор из множества решений. Кроме того, поскольку с «точки зрения» целевой функции все альтернативные решения равнозначны, можно привлечь дополнительный критерий отбора решений, который изначально не учитывался в модели. Тем самым можно улучшить решение, сделать его более оптимальным, но в соответствии с новым дополнительным критерием. Например, в рассматриваемом случае с заводом «Limited Electro» среди альтернативных решений можно найти такое решение, которое обеспечивает минимальные суммарные запасы сырья при той же величине прибыли. Легко убедиться, что при решении х1 = 500 и х2 = 0 потребуется 80000 единиц всех видов сырья, а при решении х1 = 350 и x2 = 150 — 93500. Именно по этому дополнительному критерию «Поиск решения» выделил решение х1 = 500 и х2 = 0 (см. Рисунок 18).

Создание итогового отчёта

Для подведения итогов анализа чувствительности требуется записать и структурировать информацию, которая была получена в результате этого анализа. Одним из вариантов такой формализации результатов является составление таблицы, где для тех значений параметров модели, которые изменялись при проведении анализа чувствительности, были бы приведены значения переменных решения и соответствующие значения целевой функции. В Excel построение такой таблицы может быть выполнено при помощи средства сценарии.

Сценарий — это сохраненное множество значений ячеек рабочего листа, т.е. своего рода снимок состояния. Excel имеет возможность быстрого переключения между различными сценариями. Поэтому, если сохранить в качестве сценария значения параметров модели и значения переменных решения, можно быстро восстановить табличную модель и ее решение при различных наборах параметров. Кроме того, на основе сохраненных сценариев Excel может создать отчет. Сценарии являются полезными при проведении анализа чувствительности (для сравнения различных решений) и для документирования результатов анализа.

Рассмотрим на примере, как создавать и сохранять сценарии и как на их основе затем построить отчет. Для оптимизации работы аналитика, сценарии желательно сохранять по мере их формирования, т. е. после каждого изменения, внесенного в табличную модель, а в текущей лабораторной работе, для формирования сценариев потребуется повторить несколько расчётов.

Перед началом создания сценариев требуется сделать замечание о том, что следует сохранять в сценариях. В сценариях сохраняются константы, т. е. такие значения, которые в ячейки рабочего листа введены напрямую, а не вычислены по формулам. Значения переменных решения, хотя они вычисляются с помощью средства «Поиск решения», также считаются константами, поскольку для их определения не используются формулы рабочего листа. Т.о. результаты вычислений не сохраняются, а вычисляются заново при восстановлении на рабочем листе ранее сохраненных констант сценария или при создании отчета по сценариям. В сценариях примера будем сохранять значения переменных решения, значения целевых коэффициентов и значения правых частей ограничений.

Восстановим по очереди модели. Первая модель имела целевые коэффициенты с1 и с2 соответственно 2000 и 2500, а правая часть пятого ограничения равнялась 30000. Восстановите на рабочем листе эти значения и запустите средство «Поиск решения» для получения решения. Должно получиться прежнее решение: x1 = 257, x2 = 150 и z = 889285,71 (см. Рисунок 10).

Чтобы создать новый сценарий для текущего рабочего листа, выполните следующие действия:

Выберите команду Сервис->Сценарии (в MS Office 2007 и выше — Данные->Работа с данными->Анализ «что если»).
Открывшееся диалоговое окно «Диспетчер сценариев» — основное средство работы со сценариями. В этом окне нажмите кнопку «Добавить» (см. Рисунок 20).
В диалоговом окне «Добавление сценария» введите название сценария в поле ввода «Название сценария» (см. Рисунок 21). Желательно давать содержательные названия, показывающие отличия данного сценария от других. В рассматриваемом примере первый сценарий назовите «Исходный».

Рисунок 20. Диалоговое окно «Диспетчер сценариев»

Рисунок 21. Диалоговое окно «Добавление сценария»

В поле ввода «Изменяемые ячейки» введите адреса ячеек, содержащих константы, задающие параметры модели. Эти ячейки в сценариях называются ячейки переменных. В рассматриваемом примере надо ввести B4:C4;B8:C8;F11:F17. Проще всего вводить адреса ячеек путем выделения ячеек непосредственно на рабочем листе.
В поле ввода «Примечание» желательно вводить комментарии к создаваемому сценарию. Excel автоматически создаст примечание, содержащее имя создателя сценария (по зарегистрированному имени пользователя) и дату его создания.
Нажмите в диалоговом окне «Добавление сценария» кнопку «ОК».
В открывшемся диалоговом окне Значения ячеек сценария проверьте и при необходимости измените значения для изменяемых ячеек (см. Рисунок 22).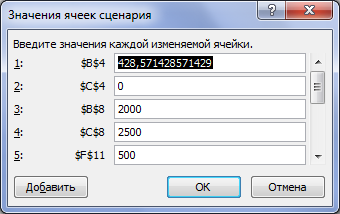

Рисунок 22. Задание значений для нового сценария

Нажмите кнопку «ОК» в диалоговом окне «Значения ячеек сценария», что создает сценарий и возвращает в диалоговое окно «Диспетчер сценариев».

Сценарий создан. Чтобы посмотреть, как сценарий вычисляет результаты (и для проверки сохраненных в сценарии значений), измените какие-либо значения на рабочем листе (например, измените значения переменных решения) и затем выполните следующие действия. Выберите команду Сервис->Сценарии (в MS Office 2007 и выше — Данные->Работа с данными->Анализ «что если»), в открывшемся диалоговом окне «Диспетчер сценариев» в списке «Сценарии» выберите сценарий, который надо отобразить, и нажмите кнопку «Вывести». Excel должен воспроизвести на рабочем листе решение первой задачи, которое отображает Рисунок 22. Если есть числовые расхождения между рисунком и воспроизведённым сценарием, то проверьте в сценарии значения изменяемых ячеек.

Далее создайте сценарий для решения, где правая часть пятого ограничения заменена значением 36500. Для этого введите в ячейку F14 данное значение и найдите решение с помощью средства «Поиск решения» (см. Рисунок 14). Затем повторите описанные выше действия по созданию сценария. Новый сценарий назовите, например, «Полная загрузка».

Подобным образом создайте сценарий, где удельные прибыли дисплеев обоих типов равны, и поэтому Excel предлагает отказаться от производства дисплеев 51” (см. Рисунок 18). Этот сценарий назовите «Без дисплеев 51”». Также создайте еще один сценарий, где удельные прибыли дисплеев разных типов также равны, но требуется произвести 150 ед. дисплеев 51” (см. Рисунок 23). Этому сценарию дайте название «С дисплеями 51”».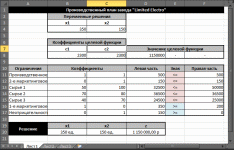

Рисунок 23. Решение с равной ценой дисплеев и полной загрузкой дисплеев 51"

Далее создайте отчет по имеющимся сценариям можно следующим образом:

Выберите команду Сервис->Сценарии (в MS Office 2007 и выше — Данные->Работа с данными->Анализ «что если»).
В открывшемся диалоговом окне «Диспетчер сценариев» нажмите кнопку «Отчет».
В диалоговом окне «Отчет» по сценарию укажите, какой тип отчета вы хотите создать: выберите переключатель «структура» для создания итогового отчета в виде структурированного рабочего листа, либо переключатель «сводная таблица» — для создания итогового отчета в виде сводной таблицы (см. Рисунок 24). Для сценариев решения задач линейной оптимизации наиболее подходит отчет в виде структурированного рабочего листа.

Рисунок 24. Диалоговое окно Отчет по сценарию

В поле ввода «Ячейки результата» введите адреса ячеек (с клавиатуры или путем выделения их непосредственно на рабочем листе), содержащих итоговые результаты. Для задач оптимизации обязательно надо указать ячейку с целевой функцией, а также, поскольку в сценариях сохраняются значения правых частей ограничений, ячейки с формулами, вычисляющими значения левых частей ограничений.
Нажмите кнопку «ОК».

Отчет по сценариям легко читается и понятен с первого взгляда, если изменяемым ячейкам сценариев и ячейкам результатов (задаваемых при создании отчета) присвоить уникальные имена, соответствующие их смыслу. Присвоить имена ячейкам можно нажав на них правой кнопкой мыши -> «Присвоить имя…». В противном случае остаются пустыми ячейки отчета в столбце В, и их возможно заполнить вручную.

Рисунок 25 отображает готовый отчет по созданным сценариям. Этот отчет в достаточной степени подходит для документирования и обоснования принятия решения. Он послужит основой для заключительных выводов выполненного анализа чувствительности.

1 2 3 4 5