симплекс метод. Лабораторная работа 3 Решение однокритериальных задач принятия решений методами линейного программирования Общие сведения
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
Практическая часть.Анализ математической модели и получение математического решения проблемы в системе Excel/Построение табличной моделиПрежде чем приступить к выполнению вычислений в MS Office Excel (далее Excel), необходимо перевести построенную математическую модель на рабочий лист Excel. Для этого следует определить, в каких ячейках будут располагаться переменные решения, записать в нужные ячейки формулы, по которым будут вычисляться целевая функция и функции ограничений (левые части ограничений), надо записать в отдельные ячейки значения правых частей ограничений. Всю эту совокупность значений и формул, записанных на рабочем листе Excel, назовем табличной моделью. Для табличных моделей задач оптимизации не существует общепринятых правил построения. Однако можно выделить некоторые рекомендации, которые облегчат дальнейшее применение средства «Поиск решения»: Значения переменных требуется располагать в отдельных ячейках и группировать в отдельный блок ячеек. Каждому ограничению требуется отводить отдельную строку или столбец таблицы. Ограничения требуется группировать в отдельный блок ячеек. Предпочтительно, чтобы ячейки, содержащие переменные и значение целевой функции, а также все ограничения, имели заголовки. Коэффициенты целевой функции должны храниться в отдельной строке, располагаясь непосредственно под или над соответствующими переменными; формула для вычисления целевой функции должна находиться в соседней ячейке. В каждой строке ограничений за ячейками, содержащими коэффициенты данного ограничения, следует ячейка, в которую записывается вычисленное значение функции ограничения (значение левой части ограничения). За ней может следовать ячейка, в которой стоит соответствующий знак неравенства или равенства ограничения, а затем ячейка, содержащая значение правой части ограничения. Желательно, чтобы правые части ограничений были константами, а не формулами. Дополнительно можно иметь ячейку, в которой вычислена разность между значениями левой и правой частей неравенства. Условия неотрицательности переменных решения не обязательно включать в табличную модель. Как правило, они опускаются и указываются непосредственно в диалоговом окне средства «Поиск решения». В результате выполнения этих рекомендаций все основные коэффициенты модели содержатся в отдельных ячейках, поэтому их легко изменять, не меняя формул модели. Благодаря группированию упрощается работа со средством «Поиск решения», поскольку для указания переменных или ограничений можно использовать диапазоны ячеек, т.е. задавать переменные и ограничения группой, а не по отдельности. Наличие заголовков сделает понятной эту табличную модель не только вам, но и прочим пользователям. Пример табличной модели для рассматриваемого примера отображает Рисунок 1. Здесь значения переменных решения записаны в ячейках В4 и С4 с соответствующими заголовками в ячейках В3 и С3. Изначально введены произвольные значения переменных. Коэффициенты, стоящие перед переменными в формуле целевой функции, записаны в ячейки В8 и С8, а само значение целевой функции вычисляется в ячейке D8 (соответствующие заголовки записаны над этими ячейками). Ниже в диапазоне В11:С17 записаны коэффициенты функций ограничений, в диапазоне D11:D17 вычисляются значения левых частей ограничений, в диапазоне Е11:Е17 записаны знаки неравенств ограничений, а в диапазоне F11:F17 — значения правых частей ограничений. Внизу, наконец, в строке 20 справа от заголовка «Решение» повторены значения переменных и целевой функции. Формулы, по которым выполняются все вычисления на данном рабочем листе, содержит Рисунок 2. Для вычисления линейных функций используется функция СУММПРОИЗВ(массив1;массив2), которая суммирует попарные произведения элементов двух диапазонов, заданных аргументами функции массив1 и массив2. Например, формула =СУММПРОИЗВ($В4:$С4;В8:С8), вычисляющая значение целевой функции в ячейке D8, эквивалентна такой формуле: =В4*В8+С4*С8. Абсолютные ссылки, которые вводятся с использованием символа «$», $В4:$С4 на диапазон В4:С4, содержащий значения переменных х1 и х2, сделаны для того, чтобы можно было скопировать эту формулу из ячейки D8 в ячейки D11:D17 для вычисления левых частей неравенств, где также участвуют значения переменных решения. 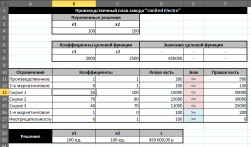 Рисунок 1. Табличная модель для вычисления производственного плана завода «Limited Electro» 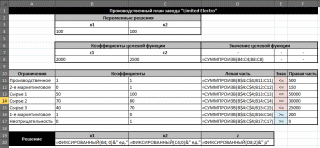 Рисунок 2. Формулы табличной модели Левые части ограничений, поскольку это линейные функции, также вычисляются с помощью функции СУММПРОИЗВ. Даже если это простые ограничения типа х2 150, которые здесь представляются как 0*x1 + 1*х2 150 (2-е маркетинговое ограничение, Рисунок 2). Требуется обратить внимание на то, что ограничения сгруппированы по типу неравенств — сначала идут ограничения типа <=, а затем типа >=. Последовательность расположения групп не существенна, однако существенно само наличие групп однотипных ограничений, что позволит в дальнейшем использовать эту группировку в средстве «Поиск решения» для более удобного использования. Знаки неравенств в диапазоне Е11:Е17 вставлены только для информативности ограничений для пользователя модели, а средство «Поиск решения» их не использует. Средство «Поиск решения» использует при построении отчётов заголовки строк, содержащих ограничения. Поэтому рекомендуется давать более содержательные заголовки, даже чем те, что содержит Рисунок 1 в ячейках А11:А17. Например, можно использовать следующие заголовки: Ограничение на объем производства, Маркетинговое ограничение продаж и т.п. С другой стороны, заголовки не являются обязательным элементом табличной модели, однако их отсутствие приводит к потере информативности модели для её пользователей. Использование средства «Поиск решения»После того, как была построена и проверена табличная модель, необходимо её решить. Для этого и используется надстройка Excel «Поиск решения». Соответствующая надстройке область меню «Анализ» должна располагаться в меню «Сервис» в (или в меню «Данные» в MS Office 2007 и выше) (см. Рисунок 3).  Рисунок 3. Панель «Анализ» и кнопка «Поиск решения» Если указанные элементы меню не найдены, требуется подключить надстройку. Для ее подключения выполните команду Сервис->Надстройки (или Файл->Параметры->Надстройки в MS Office 2007 и выше) и в открывшемся диалоговом окне Надстройки в списке Доступные надстройки установите флажок «Поиск решения». Покажем общую схему применения средства «Поиск решения» для решения задач линейного программирования. Для применения средства «Поиск решения» требуется выполнить следующие шаги (предполагается, что до первого шага на листе Excel создана и проверена табличная модель): Выберите команду «Поиск решения». В открывшемся диалоговом окне «Поиск решения» укажите данные, необходимые для поиска оптимального решения (см. Рисунок 4). В поле «Оптимизировать целевую функцию» введите адрес ячейки, содержащей значение целевой функции. Для модели из примера в это поле следует ввести D8. Параметр «До» позволяет задать тип оптимизации. В данном случае необходимо максимизировать значение целевой функции, т.е. выбрать переключатель «Максимум». Поле «Изменяя ячейки переменных» позволяет указать ячейки, в которых содержатся переменные модели. В рассматриваемом примере требуется ввести диапазон В4:С4. 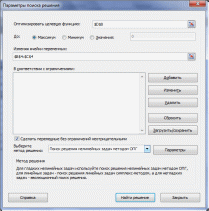 Рисунок 4. Задание параметров для поиска решения Далее задайте ограничения в области «В соответствии с ограничениями», используя кнопку «Добавить». Для рассматриваемого примера требуется ввести два элемента ограничений, как показывают Рисунок 5 и Рисунок 6. 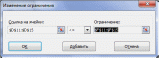 Рисунок 5. Задание первой группы ограничений 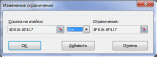 Рисунок 6. Задание второй группы ограничений После задания ограничений следует задать метод решения «Поиск решения линейных задач симплекс-методом» в поле «Выберите метод решения» (см. Рисунок 7). 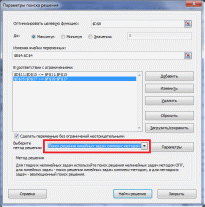 Рисунок 7. Выбор метода решения Далее требуется в диалоговом окне Параметры, которое открывается после нажатия кнопки «Параметры» диалогового окна «Поиск решения», задать дополнительные условия для поиска решения (см. Рисунок 8): Параметры «Максимальное время (в секундах)»=100, «Число итераций»=100, «Точность ограничения»= 0,000001. Установить флажок «Использовать автоматическое масштабирование». Если хотите проследить каждую итерацию процесса вычисления, установите флажок «Показывать результаты итераций». Если хотите сразу получить результат вычислений, не устанавливайте этот флажок. 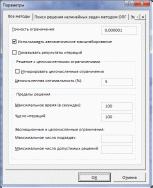 Рисунок 8. Параметры поиска решения Все прочие параметры предназначены для настройки решений с использованием методов решения нелинейных задач и эволюционного поиска. Нажмите кнопку «Найти решение». После окончания работы «Поиск решения» выведет на экран диалоговое окно «Результаты поиска решения» (см. Рисунок 9), в котором можно указать дальнейшие действия. Выберите все отчёты для их дальнейшего построения и нажмите кнопку «ОК». 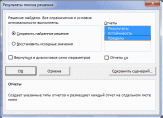 Рисунок 9. Успешное завершение решения задачи. Диалоговое окно «Результаты поиска решения» сообщает о завершении поиска. Если оптимальное решение найдено, в диалоговом окне «Результаты поиска решения» должно отобразиться сообщение «Решение найдено. Все ограничения и условия оптимальности выполнены». Если получено такое сообщение, можно или сохранить найденное решение, выбрав соответствующий параметр, или отбросить его, выбрав параметр «Восстановить исходные значения». Существует возможность также получить три типа отчетов о решении. Каждый отчет выводится на новый лист рабочей книги. В рассматриваемом примере решение найдено (см. Рисунок 10): надо производить 257 единиц дисплеев типа 46” и 150 единиц дисплеев типа 51”, при этом будет получена прибыль в размере 889 285,17 руб. В диалоговом окне Результаты поиска решения мы также указали, что надо создать отчеты. 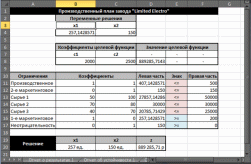 Рисунок 10. Решение линейной модели для завода «Limited Electro» |
