Лекции Булатицкий Дмитрий Иванович (во многом по материалам Прасолова А. Н.)
 Скачать 319.62 Kb. Скачать 319.62 Kb.
|
РекурсияПонятие рекурсииРеку́рсия — в определении, описании, изображении какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. Рекурсия в математикеВ математике рекурсия имеет отношение к методу определения функций и числовых рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой с другими аргументами. При этом возможно два варианта: Конечная рекурсивная функция. Она задаётся таким образом, чтобы для любого конечного аргумента за конечное число рекурсивных обращений привести к одному из отдельно определённых частных случаев, вычисляемых без рекурсии. Классический пример: рекурсивно-определённый факториал целого неотрицательного числа. 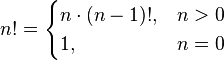 Бесконечная рекурсивная функция. Она задаётся в виде обращения к самой себе во всех случаях (по крайней мере, для некоторых из аргументов). Подобным образом могут задаваться бесконечные ряды, бесконечные непрерывные дроби и так далее. Практическое вычисление точного значения здесь, естественно, невозможно, поскольку потребует бесконечного времени. Требуемый результат находится аналитическими методами. Тем не менее, если речь идёт не о получении абсолютно точного значения, а о вычислении заданного приближения искомого значения, то тут в некоторых случаях возможно прямое использование рекурсивного определения: вычисления по нему ведутся до тех пор, пока необходимая точность не будет достигнута. Примером может служить один из вариантов разложения числа Эйлера: 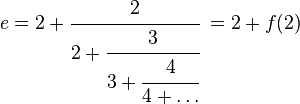 Прямой расчёт по приведённой формуле вызовет бесконечную рекурсию, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу. Другим распространённым примером рекурсии является ряд, получивший название Числа Фибоначчи. Рекурсия в физикеКлассическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал. Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы. Рекурсия в литературе«У попа была собака, он её убил…» Рекурсия (от латинского recursio - возвращение) - это такой способ организации вычислительного процесса, при котором процедура или функция в ходе выполнения составляющих ее операторов обращается сама к себе. Для того, чтобы такое обращение не было бесконечным, в тексте подпрограммы должно быть условие, по достижению которого дальнейшего обращения не происходит. таким образом, рекурсивное обращение может включаться только в одну из ветвей подпрограммы. В языке Си нет никаких ограничений на рекурсивные вызовы подпрограмм, необходимо только понимать, что каждый очередной рекурсивный вызов приводит к образованию новой копии локальных объектов подпрограммы и все эти копии, соответствующие цепочке активизированных и не завершенных рекурсивных вызовов, существуют независимо друг от друга. В правильно организованной рекурсивной функции должно быть одно или несколько граничных условий, при которых значение функции известно. В зависимости от способа рекурсивного вызова различают прямую и косвенную рекурсию. Примеры Снежинка Коха Пример в зелёной папке |
