эссе информатика. Информатика тема 2 Лекция Подходы к измерению информации. Лекции обязателен к изучению
 Скачать 33.09 Kb. Скачать 33.09 Kb.
|
|
Лекция Подходы к измерению информации Материал лекции обязателен к изучению Вероятностный подход Зачастую, получившие одно и то же сообщение люди, по-разному оценивают информацию, содержащуюся в нем. Те, кто мало осведомлен об описываемых событиях, сочтут, что получил много информации. Те, кто имел сведений больше, чем получили в сообщении, скажут, что информации не получили вовсе. С каждым получаемым сообщением неопределенность знаний по интересующему вопросу уменьшается. Если достигнута полная ясность, то неопределенность исчезает. Таким образом, информацию, которую получает человек, можно считать мерой уменьшения неопределенности знания. При таком подходе, бит- это единица количества информации, уменьшающая неопределенность знаний человека в два раза. В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Предложенная им формула имела следующий вид: I = log2 K где К - количество равновероятных событий; I - количество бит в сообщении, такое, что любое из К событий произошло. Тогда K=2I. Иногда формулу Хартли записывают так: I = log2 K = log2 (1 / р) = - log2 р т. к. каждое из К событий имеет равновероятный исход р = 1 / К, то К = 1 / р. Задача. Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В. Решение. Такое сообщение содержит I = log2 3 = 1,585 бита информации. Но не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. В 1948 г. американский инженер и математик К. Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями. Если I - количество информации, N - Количество возможных событий, рi - вероятности отдельных событий, то количество информации для событий с различными вероятностями можно определить по формуле: I = - Sum рi log2 рi, Если произошло событие i, мы получаем информацию Рисунок I = log2 K = log2 (1 / рi) Формулу Хартли теперь можно рассматривать как частный случай формулы Шеннона: I = - Sum 1 / N log2 (1 / N) = I = log2 N. При равновероятных событиях получаемое количество информации максимально. Физиологи и психологи научились определять количество информации, которое человек может воспринимать при помощи органов чувств, удерживать в памяти и подвергать обработке. Информацию можно представлять в различных формах: звуковой, знаковой и др. Рассмотренный выше способ определения количества информации, получаемое в сообщениях, которые уменьшают неопределенность наших знаний, рассматривает информацию с позиции ее содержания, новизны и понятности для человека. С этой точки зрения в опыте по бросанию кубика одинаковое количество информации содержится в сообщениях "два", "вверх выпала грань, на которой две точки" и в зрительном образе упавшего кубика. Лекция Подходы к измерению информацииМатериал лекции обязателен к изучению Объемный подходПри передаче и хранении информации с помощью различных технических устройств информацию следует рассматривать как последовательность знаков (цифр, букв, кодов цветов точек изображения), не рассматривая ее содержание. Считая, что алфавит (набор символов знаковой системы) - это событие, то появление одного из символов в сообщении можно рассматривать как одно из состояний события. Если появление символов равновероятно, то можно рассчитать, сколько бит информации несет каждый символ. Информационная емкость знаков определяется их количеством в алфавите. Чем из большего количества символов состоит алфавит, тем большее количество информации несет один знак. Полное число символов алфавита принято называть мощностью алфавита. Молекулы ДНК (дезоксирибонуклеиновой кислоты) состоят из четырех различных составляющих (нуклеотидов), которые образуют генетический алфавит. Информационная емкость знака этого алфавита составляет: 4 = 2I, т.е. I = 2 бит. Каждая буква русского алфавита (если считать, что е=ё) несет информацию 5 бит (32 = 2I). При таком подходе в результате сообщения о результате бросания кубика, получим различное количество информации. Чтобы его подсчитать, нужно умножить количество символов на количество информации, которое несет один символ. Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе, подсчитывается просто по количеству требуемых для такой записи двоичных символов. Для измерения больших объемов информации пользоваться битами неудобно. Поэтому применяются кратные биту единицы измерения информации: 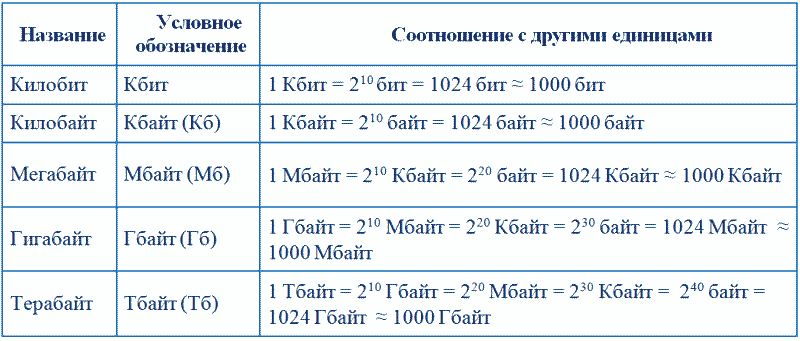 Пример 1. Сколько места в памяти надо выделить для хранения предложения Привет, Петя! Решение. Считаем все символы, включая знаки препинания и пробелы (здесь 13 символов). Если нет дополнительной информации, то считаем, что 1 символ занимает 1 байт в кодировке UNICODE 1 символ занимает 2 байта. Ответ: 13 байт или 104 бита (в UNICODE: 26 байт или 208 бит) Пример 2. Сколько места надо выделить для хранения 50 страниц книги, если на каждой странице помещаются 32 строки по 64 символа в каждой? Решение: на 1 странице 32·64=2048 символов на 50 страницах 50·2048=102400 символов каждый символ занимает 1 байт. Ответ: 102400 байт 102400·8 бит=819200 бит 102400:1024 Кбайт = 100 Кбайт Пример 3. Сколько байт памяти необходимо, для хранения 256-цветного рисунка размером 64 на 128 пикселя? Решение: общее число пикселей: 64*128=8192 при использовании 256 цветов на 1 пиксель отводится 8 бит (выбор 1 из 256 вариантов) Ответ: 8192·8 бита = 65536 бит =8192 байт … 8192:1024 Кбайт = 8 Кбайт Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в вероятностном (кибернетическом) смысле, но заведомо допускает его в объемном. Далее, если некоторое сообщение допускают измеримость количества информации в обоих смыслах, то это количество не обязательно совпадает, при этом кибернетическое количество информации не может быть больше объемного. В прикладной информатике практически всегда количество информации понимается в объемном смысле. |
