Лекции по курсу сопротивление материалов

• Название: Лекции по курсу сопротивление материалов
• Дата: 29.11.2021
• Размер: 1.05 Mb.
• Имя файла: LEKTsII_PO_SM-1s.doc
• Тип: Лекции; #285343
• страница: 3 из 7

Закон парности касательных напряжений
В окрестностях произвольной точки напряженного тела выделим элементарный объём в форме прямоугольного параллепипеда со сторонами dx, dy, dz. На каждой из граней действует по три составляющих напряжения: нормальное напряжение и два касательных (рис.20).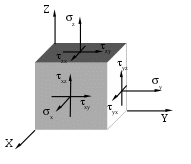



Рис.20
Составим уравнение равновесия выделенного элемента в форме суммы моментов всех сил относительно оси X:
М_х = 0,

_уdxdzdy - _уdxdzdy + _zdxdydz - _zdxdydz + _xydydz - _xydydz +

+ _xzdydz - _xzdydz + _zydxdydz - _yzdxdzdy = 0,
приведя подобные слагаемые и упростив выражение, получим:
_zy = _yz. (29)
Составляя уравнения равновесия относительно осей Y и Z, получим аналогичные выражения:
_zх = _хz, (30)

_хy = _yх.
Полученные выражения (29), (30) определяют закон парности касательных напряжений: касательные напряжения на взаимно перпендикулярных площадках равны по величине и направлены либо к общему ребру, либо от него.
Напряжения на наклонных площадках
Элементарный объём в форме параллепипеда, связанный с системой координат таким образом, чтобы его грани совпадали с координатными плоскостями, рассечем наклонной плоскостью (рис.21).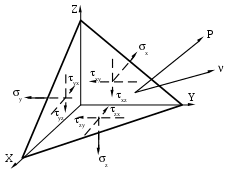



Рис.21
Положение наклонной площадки характеризуется вектором нормали  с направляющими косинусами l, m, n. На наклонной площадке площадью dF действует полное напряжение Р с проекциями по осям Р_х, Р_у, Р_z. Пусть нормальные и касательные напряжения на гранях, совпадающих с координатными плоскостями, известны. Необходимо найти нормальное и касательное напряжение на наклонной площадке - _ и _. Площадки, отсекаемые на координатных плоскостях, будут иметь площади:
dF_x = dFl, dF_y = dFm, dF_z = dFn.
Составим уравнение равновесия сил в проекции на ось Х:

Х = 0,

P_xdF - _xdF_x - _yxdF_y - _zxdF_z = 0,

P_xdF - _xdFl - _yxdFm - _zxdFn = 0,

P_x = _xl + _yxm + _zxn. (31)
Аналогично, составляя уравнения равновесия сил на оси Y и Z, получаем выражения для двух других проекций полного напряжения:
P_y = _xyl +_ym + _zyn,

P_z = _xzl + _yzm +_zn. (32)
Чтобы определить нормальное напряжение на наклонной площадке, спроецируем проекции полного напряжения на нормаль.
_ = P_xl + P_ym + P_zn =

= _xl² + _yxml + _zxnl + _xylm +_ym² + _zynm + _xzln + _yzmn +_zn²
С учетом закона парности касательных напряжений - (29) и (30), получаем основную квадратичную форму нормальных напряжений:
_ = _xl² + _ym² +_zn² + 2_yxml + 2_zxnl + 2_zynm (33)
Полученное выражение позволяет определить нормальное напряжение на любой наклонной площадке, поскольку при выводе этого выражения никаких ограничений на положение площадки не накладывалось. Теперь найдем величину касательного напряжения на наклонной площадке:
Р² = P_x² + P_у²+ P_z² = _² + _²,

_²= P_x² + P_у²+ P_z² - _². (34)
Главные площадки и главные напряжения
Нормальные и касательные напряжения на наклонной площадке зависят от ее положения, то есть от направляющих косинусов l, m, n.

Площадки, на которых касательные напряжения равны нулю и действуют только нормальные напряжения, называются главными. Нормальные напряжения на этих площадках называются главными напряжениями.

Предположим, что наклонная площадка с направляющими косинусами l, m, n является главной, то есть вектор нормали к наклонной площадке совпадает с вектором полного напряжения. Тогда нормальное напряжение на этой площадке равно полному напряжению, а касательное напряжение равно нулю (рис.22). Проекции полного напряжения на координатные оси равны:
P_x = l, P_у = m, P_z = n.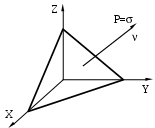



Рис.22
Используя выражения, полученные для наклонной площадки, - (31) и (32), имеем:
P_x = _xl + _yxm + _zxn = l,

P_у = _xyl + _ym + _zyn = m,

P_z = _xzl + _yzm + _zn = n.
В данных уравнениях четыре неизвестных (направляющие косинусы l, m, n и главное напряжение ), поэтому необходимо четвертое уравнение:
( _x - )l + _yxm + _zxn = 0

_xyl + (_y - )m + _zyn = 0 (35)

_xzl + _yzm + (_z - )n = 0

l² + m² + n² = 1
Система уравнений имеет ненулевое решение (нулевое не устраивает из-за четвертого уравнения системы), когда равен нулю главный определитель системы:
 _x -  _yx _zx

_xy _y -  _zy = 0 (36)

_xz _yz _z - 
Раскроем определитель
(_x - )(_y - )(_z - ) + _yx_zy_xz + _xy_yz_zx - _xz(_y - )_zx - _xy_yx(_z - ) -

- _yz_zy(_x - ) = 0.
_x_y_z - _y_z - _x_z + ²_z - _x_у + ²_у + ²_х - ³ + 2_xy_yz_zx –

- _y_xz² + _xz² - _z_xу² + _xу² - _х_уz² + _уz² = 0.
Сгруппируем слагаемые по степеням главного напряжения

- ³ + ²(_x + _y + _z) - (_y_z + _x_z + _x_у - _xz² - _xу² - _уz²) +

+ (_x_y_z + 2_xy_yz_zx - _y_xz² - _z_xу² - _х_уz²₎ = 0.
Запишем это уравнение в более компактной форме
³ – I₁² + I₂ – I₃ = 0 (37)

где I₁ = _x + _y + _z,

I₂ = _y_z + _x_z + _x_у - _xz² - _xу² - _уz²,

I₃ = _x_y_z + 2_xy_yz_zx - _y_xz² - _z_xу² - _х_уz² .
Введенные обозначения называются инвариантами напряженного состояния. Так как главные напряжения в точке являются физической характеристикой, то они не зависят от выбора системы координат, а, следовательно, и значения инвариантов также не зависят от выбора системы координат.

Решая кубическое уравнение (37), получим три вещественных корня – три главных напряжения, которые нумеруются в порядке убывания: ₁  ₂  ₃. Подставляя величину главного напряжения в систему (35), можно определить положение главной площадки, т.е. определить ее направляющие косинусы. Три главных площадки в точке взаимно перпендикулярны.
Экстремальные свойства главных напряжений.

Круговая диаграмма Мора
Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение.

Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис.23), то в наклонной площадке с вектором нормали  (l, m, n) возникают нормальные и касательные напряжения Р(, ). Определим эти напряжения и исследуем их экстремальные свойства.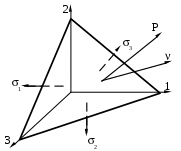




Рис.23
Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:

_ = ₁l² + ₂m² + ₃n² (38)
Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):
Р² = P_х²+ P_у² + P_z² = ₁²l² + ₂²m² + ₃²n² (39)
Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17).

Таким образом, мы имеем систему трех уравнений с тремя неизвестными - l², m², n²: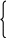
 = ₁l² + ₂m² + ₃n²

² + ² = ₁²l² + ₂²m² + ₃²n² (40)

1 = l² + m² + n²
Умножим каждое уравнение на произвольные множители a, b, c и сложим, сгруппировав при этом слагаемые по направляющим косинусам
а + b(² + ²) + с =

= l²(а₁ + b₁² + с) + m ²(а₂ + b₂² + с) + n ²(а₃ + b₃² + с) (41)
Для определения величины l² подберем коэффициенты a, b, c таким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:
а₂ + b₂² + с = 0,

а₃ + b₃² + с = 0,

получаем
b = 1, а = -(₂ +₃), с = ₂₃.
Подставляя полученные коэффициенты в уравнение (41), находим величину l²:
l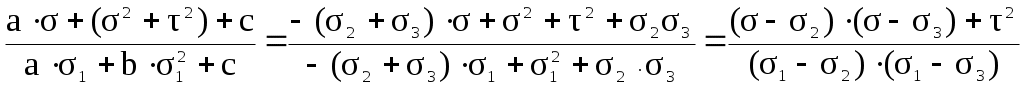²= . (42)
Аналогично находим квадраты двух других направляющих косинусов
m ² = ,

(43)

n ² = .
В уравнениях (42) и (43) дроби должны быть больше нуля, так как в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства ₁  ₂  ₃:
 0,

 0, (44)

 0.
На основе неравенств (44) можно сделать вывод о знаке числителя: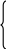




 0,

 0, (45)

 0.
Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис.24):
(46)
Представим решение системы (45) графически (рис.25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.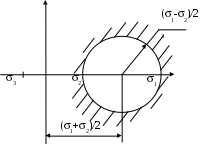


_



_


Рис.24
₁ - максимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;

₃ - минимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;

_max = 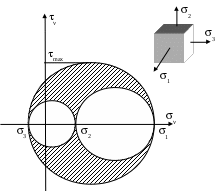- максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45.




Рис.25

Испытания материалов на растяжение. Диаграмма растяжения
При проектировании строительных конструкций, машин и механизмов инженеру необходимо знать значения величин, характеризующих прочностные и деформационные свойства материалов. Их можно получить путем механических испытаний, проводимых в экспериментальных лабораториях на соответствующих испытательных машинах. Таких испытаний проводится много и самых различных – испытания на твердость, сопротивляемость ударным и переменным нагрузкам, противодействие высоким температурам и т.д. Подробное описание всех видов механических испытаний и применяемых при этом машин и приборов приводится в специальной литературе. Мы же рассмотрим лишь испытания металлов на растяжение.

Наибольшую информацию о механических свойствах металлов можно получить из статических испытаний на растяжение. Испытания проводятся в соответствии с ГОСТом.

Для испытания на растяжение применяют образцы специальной формы – цилиндрические (рис.26). Образцы имеют рабочую часть с начальной длиной l₀, на которой определяется удлинение, и головки с переходным участком, форма и размеры которых зависят от способов их крепления в захватах машины. Различают длинные образцы с отношением l₀/d₀=10 и короткие - l₀/d₀=5. Размеры образцов делают стандартными для того, чтобы результаты испытаний, полученные в разных лабораториях, были сравнимы.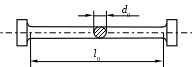




Рис.26
Испытания проводят на разрывных или универсальных машинах. В зависимости от метода приложения нагрузки машины бывают с механическим или гидравлическим приводом. Они обычно выпускаются с вертикальным расположением образца. Передача усилия на образец осуществляется через захваты. Разрывная машина снабжена устройством для автоматической записи в определенном масштабе диаграммы растяжения, т.е. графика зависимости между растягивающей силой Р и удлинением образца l. На рис.27 представлена диаграмма растяжения образца из низкоуглеродистой стали.

В начальной стадии нагружения до некоторой точки А диаграмма растяжения представляет собой наклонную прямую, что указывает на пропорциональность между нагрузкой и деформацией – справедливость закона Гука.

P


E


K


Д


В

С


A


P_т

Р_max

Р_к

P_пц

P_уп


O

l


Рис.27
Нагрузка, при которой эта пропорциональность еще не нарушается, на диаграмме обозначена Р_пц и используется для вычисления предела пропорциональности:
_пц= , (47)
где F₀ – начальная площадь поперечного сечения образца.