Лекции по курсу сопротивление материалов

• Название: Лекции по курсу сопротивление материалов
• Дата: 29.11.2021
• Размер: 1.05 Mb.
• Имя файла: LEKTsII_PO_SM-1s.doc
• Тип: Лекции; #285343
• страница: 2 из 7

Геометрические характеристики сложных сечений
При вычислении геометрических характеристик сложных сечений последние обычно разбивают на отдельные простые части, геометрические характеристики которых известны (для простых фигур они приведены в справочниках). Из основного свойства интеграла суммы следует, что геометрические характеристики сложной фигуры равны сумме геометрических характеристик её составных частей. Заметим, что в случае, когда в сечении имеется отверстие, его геометрические характеристики необходимо вычитать. Также следует учесть, что суммирование или вычитание геометрических характеристик можно производить только в том случае, если они посчитаны относительно одних и тех же осей. Поэтому, если оси простых фигур не совпадают, предварительно необходимо, используя формулы параллельного переноса (10), пересчитать геометрические характеристики относительно одной и той же оси.

Пример. Определить положение главных центральных осей и значения геометрических характеристик относительно них для сложного сечения представленного на рис.12.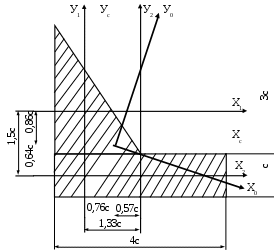



















Рис.12
Разобьем данное сечение на элементарные фигуры, геометрические характеристики которых известны по справочникам. Оси Х₁У₁ – центральные оси первой фигуры. Оси Х₂У₂ – центральные оси второй фигуры.
1 фигура - треугольник:

F₁=

S_x1=0

S_y1=0

I_x1=

I_y1=
I_x1y1=-
2 фигура - прямоугольник:

F₂ = bh = 4c∙c = 4c²

S_x2=0

S_y2=0

I_x2=

I_y2=

I_x2y2=0

Заметим, что центробежный момент инерции прямоугольника равен нулю, т. к. фигура имеет ось симметрии.

За вспомогательные оси, относительно которых вычисляем координаты центра тяжести всего сечения, принимаем Х₁У₁.
Х_с= =

У_с= = - 0,86c
По полученным значениям координат центра тяжести находим положение центральных осей всего сечения.

Найдем геометрические характеристики всего сечения относительно центральных осей. Так как оси параллельны, воспользуемся формулами преобразования при параллельном переносе осей.
S_xс=0

S_yс=0

I_xc =

=(1,5с⁴ + (0,86с)²∙3с²) + (0,33с⁴ + (-0,64с)²∙4с²) = 5,69с⁴

I_yc =

=(0,67с⁴ + (-0,76с)²∙3с²) + (5,33с⁴ + (0,57с)²∙4с²) = 9,03с⁴

I_xcyc =

=(-0,5с⁴ + (0,86с)∙(-0,76с)∙3с²) + (0 + (-0,64с)∙(0,57с)∙4с²) = -3,92с⁴
Найдем положение главных центральных осей сечения. Для этого определяем угол поворота центральных осей.
tg2= = – 2,35,

=0,5arctg(- 2,35) = - 33,5°.
Так как получили отрицательный угол, то поворачиваем центральные оси по часовой стрелке.

Найдем значения геометрических характеристик относительно главных центральных осей сечения Х₀У₀:
I_х0= I_хccos² - I_хcуcsin2 + I_уcsin² = 5,69с⁴ ∙cos²(-33,5) + 3,59c⁴∙sin(-67) + 9,03с⁴∙sin²(- 33,5) = 3,4с⁴ ;

I_у0= I_yccos² + I_хcуcsin2 + I_xcsin² = 9,03с⁴∙ cos²(-33,5) – 3,59c⁴∙sin(-67) + 5,69с⁴∙ sin²(- 33,5) = 11,32с⁴;

I_х0у0= I_хcуccos2 - 0,5sin2(I_yc - I_xc) = - 3,92 cos(-67) – 0,5sin(-67)(9,03с⁴ – 5,69с⁴) = 0.
Статические моменты инерции сечения при повороте осей проходящих через центр тяжести не меняются и остаются равными нулю.
Метод сечений. Внутренние силы
Для изучения внутренних явлений в теле используется метод сечений.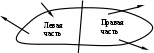







Рис.13
Все тело находится в равновесии. После мысленного разрезания и отбрасывания правой части её действие должно быть заменено системой сил (рис.13) в сечении, сохраняющих равновесие левой части. Такие же силы, но противоположного направления действуют на правую часть.

Для удобства приводим все силы, действующие в сечении, к центру тяжести; в результате этого получается главный вектор сил и главный вектор моментов (рис.14).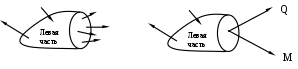


Рис.14
Разложим главные вектора по осям в правой системе координат: Q (Q_x, Q_y, Q_z); M (M_x, M_y, M_z) (рис.15).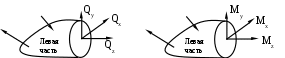



Рис.15
Проекции имеют определенные названия: Q_x, Q_y – поперечные силы; Q_z – продольная сила; M_x, M_y – изгибающие моменты; M_z – крутящий момент.

Сила считается положительной, если ее направление совпадает с осью, момент считается положительным, если он создает вращение против часовой стрелки (смотреть необходимо с конца соответствующей оси). Эти шесть проекций называют интегральными характеристиками напряжений.

Всё тело до рассечения находилось в равновесии. Так как силы, действующие в сечении, заменяют действие отброшенной части, то и оставшаяся часть должна находится в равновесии, следовательно, к ней применимы уравнения статики.
Х=0,

Р_1х + Р_2х + …+ Q_х = 0,

Q_х = - (Р_1х + Р_2х + …).
Проекция главного вектора внутренних сил на ось Х равна сумме проекций на эту ось всех внешних сил, действующих на левую часть, взятых с противоположными знаками. Аналогично получаем выражения для остальных проекций главного вектора внутренних сил и главного вектора момента внутренних сил.
Q_у = - (Р_1у + Р_2у + …),

Q_z = - (Р_1z + Р_2z + …),

M_х = - (M_хp1 + M_хp2 + …), (15)

M_у = - (M_уp1 + M_уp2 + …),

M_z = - (M_zp1 + M_zp2 + …).
Полученные уравнения дают лишь интегральные характеристики внутренних сил, но не дают информации о распределении сил по сечению.
Напряжение. Напряженное состояние в точке тела
Нагруженное тело мысленно рассечем плоскостью, и действие отброшенной части заменим действием внутренних сил. В сечении выберем произвольную точку, а в её окрестности элементарную площадку F. Равнодействующую сил, действующих на площадку, обозначим Р (рис.16).




Рис.16
Среднее полное напряжение на заданной площадке будет равно:
Р_ср = .
Если площадку уменьшать, то в пределе она обратится в точку. Напряжение - это предел отношения внутренней силы к площади, на которой она действует при условии, что площадь стремится к нулю. Р – полное напряжение [Н/м²].
P = lim_F0 . (16)
Вектор полного напряжения можно разложить на проекции (рис.17). Проекцию полного напряжения на нормаль к плоскости сечения будем называть нормальным напряжением (обозначается ), а проекцию полного напряжения на плоскость сечения – касательным напряжением (обозначается ). Вектор нормали к сечению обозначим через .
Р = 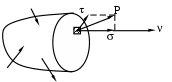(17)

Рис.17
Направление касательного напряжения не однозначно, что создает неудобство при математической обработке, поэтому его раскладывают по координатным осям в плоскости сечения. Возьмем правую систему координат. Тело рассечем перпендикулярно оси Z (рис.18).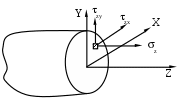



Рис.18
=
Индекс нормального напряжения соответствует оси, перпендикулярной плоскости сечения. Индексы касательного напряжения проставляются следующим образом: первый индекс соответствует оси, перпендикулярной плоскости сечения, в котором лежит касательное напряжение, второй индекс соответствует оси, которой параллельно касательное напряжение.

Проводя другие плоскости, будем получать другие значения напряжений. Совокупность напряжений по всем плоскостям, проходящим через заданную точку, называется напряженным состоянием в точке тела.

В общем случае в точке твердого деформированного тела может возникнуть 9 напряжений: 3 нормальных и 6 касательных. Эти напряжения образуют тензор напряжений: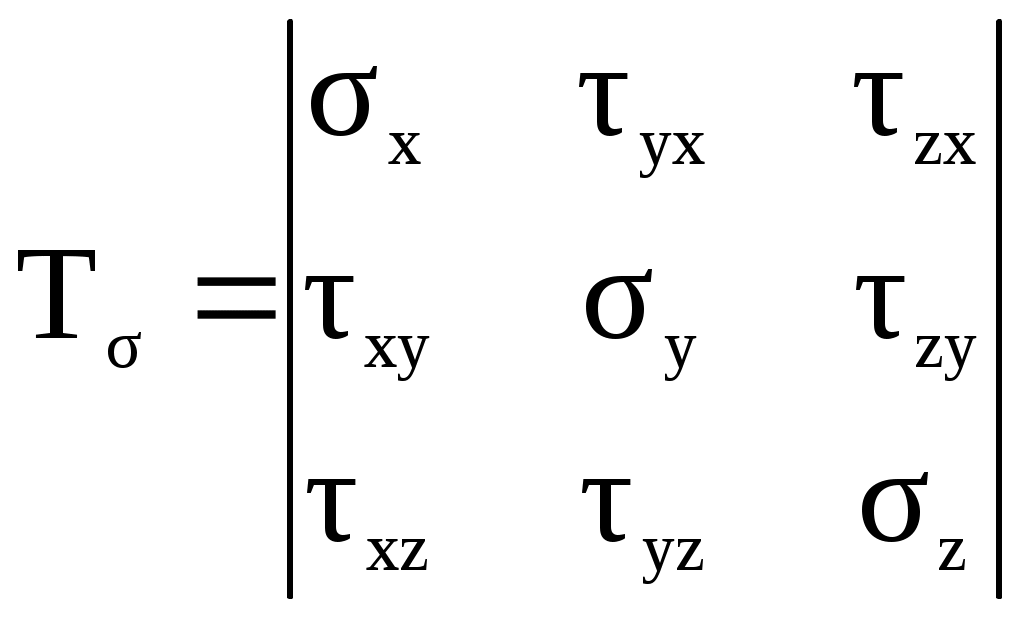
(18)
Интегральные характеристики напряжений в точке
Установим связь между интегральными характеристиками напряжений и напряжениями в сечении.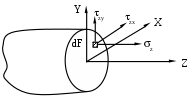




Рис.19
Выберем бесконечно малую площадку dF = dxdy. На этой площадке действуют нормальное напряжение _z и касательные напряжения _zx, _zy (рис.19). Для того, чтобы найти элементарную продольную силу, необходимо умножить нормальное напряжение на площадь площадки, на которой оно действует (_zx, _zy перпендикулярны оси Z и поэтому не входят в состав продольной силы). Так как таких элементарных площадок по сечению бесконечно много, то, чтобы найти полную продольную силу, необходимо проинтегрировать элементарную продольную силу по площади поперечного сечения:
dN=_zdxdy,

N= . (19)
Аналогично поступаем для получения выражений поперечных сил:
Q_x= ,

Q_y= . (20)
Для получения выражений изгибающих и крутящего моментов напомним, что момент - это произведение силы на плечо (плечо - это кратчайшее расстояние от оси до линии действия силы). Вокруг оси Х момент создает только сила _zdxdy (сила _zхdxdy не создает момент, так как параллельна оси Х; сила _zуdxdy не создает момент, так как пересекает ось), плечом для этой силы является координата Y точки действия силы. Момент положительный, так как создает вращение против часовой стрелки:

M_x = . (21)
Аналогично поступаем для получения выражений моментов M_у и M_z:
M_у =- , (22)

М_z = . (23)
Нормальные напряжения в плоскости поперечного сечения
Определим величину нормального напряжения в плоскости поперечного сечения, зная интегральные характеристики в этом сечении. Предположим, что нормальные напряжения в сечении распределены по линейному закону:
(х,у) = а + bх + су (24)
С нормальным напряжением в сечении связаны продольная сила и два изгибающих момента. Подставим в выражения (19), (21) и (22) наше предположение о линейной зависимости напряжения от координат в сечении (24):
N = = =

= + + =

= аF+bS_y+cS_x

M_x = = =

= + + = aS_x+bI_xy+cI_x (25)

M_у = - = - =

= - - - = -aS_y-bI_y-cI_xy
Выражения (25) были получены для произвольного положения осей. Их можно упростить, взяв в качестве системы координат главные центральные оси. По определению в этих осях статические и центробежный моменты инерции равны нулю (S_x= S_у= 0, I_xy=0).
N = аF

M_x = cI_x (26)

M_у = -bI_y
Из полученных выражений можно найти коэффициенты а, b и с:
а = N/F, с = M_x /I_x , b = -M_у /I_y (27)

Подставив полученные значения коэффициентов в наше предположение о распределении нормального напряжения по сечению (24), получим
 = , (28)
где N – продольная сила в сечении; М_х, М_у – изгибающие моменты в сечении; F – площадь поперечного сечения; I_х, I_у – главные осевые моменты инерции сечения; х, у – координаты точки, в которой вычисляется напряжение относительно главных центральных осей.