Лекции по курсу сопротивление материалов

• Название: Лекции по курсу сопротивление материалов
• Дата: 29.11.2021
• Размер: 1.05 Mb.
• Имя файла: LEKTsII_PO_SM-1s.doc
• Тип: Лекции; #285343
• страница: 1 из 7

ЛЕКЦИИ ПО КУРСУ
«СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»


Основные понятия и определения
Курс «Сопротивления материалов» является частью общей науки механики. Теоретическая механика изучает материальную точку и абсолютно твердое тело. Теория упругости изучает твердые тела, гидравлика – жидкости, аэрогазодинамика – газообразные вещества.

Объект изучения всех этих разделов – сплошная среда (равномерно распределенная по всему объему), следовательно, применение математического анализа и как следствие хорошее знание математики необходимо. В курсе «Сопротивление материалов» изучают твердые деформируемые тела, т.е. меняющие размеры и форму под действием нагрузок.

Сопротивление материалов – наука о прочности, жесткости, устойчивости и надежности инженерных конструкций.

Целью курса является разработка инженерных методов расчета конструкций и их деталей, а также методов изучения свойств материалов.

Прочность – свойство деталей и конструкций выдерживать рабочие нагрузки без разрушения или пластических деформаций.

Жесткость – свойство конструкций или деталей выдерживать рабочие нагрузки без значительных деформаций, нарушающих их нормальную работу.

Кроме прочности и жесткости конструкции и детали должны удовлетворять следующим требованиям:

1. 
   Вибростойкость - способность работать, не вступая в резонанс с возмущающими воздействиями.
   
2. 
   Вибропрочность – свойство деталей работать, не разрушаясь в условиях вибрации.
   
3. 
   Устойчивость - свойство возвращаться в исходное состояние после устранения возмущающих воздействий.
   
4. 
   Технологичность - свойство детали, которое позволяет изготавливать её экономичными высокопроизводительными методами.
   
5. 
   Современный дизайн.
   

Некоторые положения теоретической механики остаются справедливыми и для деформированного тела:

например: 6 уравнений равновесия (рис.1);



X = 0, L_x = 0,

Y = 0, L_y = 0,

Z = 0, L_z = 0.

Рис.1

Но и есть различия, в теоретической механике не рассматриваются процессы внутри тела.

Пример.

Рис.2
В теоретической механике силы можно переносить вдоль линии действия (рис.2), с точки зрения механики деформированного тела сжатие и растяжение - совершенно разные вещи;

Пример.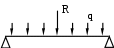



Рис.3
С точки зрения теоретической механики все силы можно заменять одной равнодействующей (рис.3), а в механике деформированного тела этого делать нельзя, так как при этом будут различные деформации.

При рассмотрении данного курса будем различать следующие виды внешних нагрузок: поверхностные силы, массовые или объемные силы.

Поверхностные - это те силы, которые приложены к поверхности тела. Источник этих сил – силы взаимодействия с другими телами. Эти силы характеризуются вектором напряженности (интенсивности) поверхностных сил.



|q| = [Н/м²] = Па,

1 Па = 0,109 кг/м² – очень малая величина,

поэтому обычно пользуются [МПа].
Рис.4
В качестве системы координат выбираем правую декартову систему, т.е. если смотреть с конца одной из стрелок, то поворот по алфавиту между двумя другими осями происходит против часовой стрелки. Вектор интенсивности можно разложить по координатным осям: q (q_x, q_y, q_z).

Если нагрузка распределена вдоль узкой полосы (рис.5), то интенсивность такой поверхностной нагрузки будет измеряться в [Н/м].




Рис.5

Если нагрузка распределена на небольшой площадке (рис.6), то интенсивность такой поверхностной нагрузки будет измеряться в [Н] и в этом случае силу можно считать сосредоточенной.



Рис.6
Массовые силы приложены к каждой частице тела и возникают в результате взаимодействия с полем.

Пример.

Гравитационное поле: |R| = [Н/м³] R (X,Y,Z).

Нагрузки также бывают статическими и динамическими. Статические – нагрузки, медленно изменяющиеся во времени. Динамические – нагрузки, быстро меняющие свою величину во времени.
Физическая и математическая модель
Физическая модель – упрощенное представление объекта или явления, сохраняющая основные его черты. Применительно к расчетам на прочность и жесткость физическая модель должна отражать: геометрические свойства детали, свойства материала детали, действующие на деталь нагрузки.

По геометрическим признакам все тела делятся на три группы:

1. 
   стержни – тела, у которых одно измерение существенно больше двух других (характеризуются поперечным сечением и формой оси).
   
2. 
   пластины и оболочки – тела, у которых одно измерение существенно меньше двух других (характеризуются толщиной и формой серединной поверхности).
   
3. 
   массивы – тела, у которых все три измерения соизмеримы.
   

Реальные конструкционные материалы (стали, чугуны, цветные материалы) имеют кристаллическое строение; кристаллы малы и расположены хаотично. Сложность реального строения и возникающая трудность при математическом его описании явились причиной разработки модели твердого тела. Эта модель должна сохранить основные свойства материалов и в тоже время сделать простым их аналитическое описание. Поэтому в расчетах на прочность и жесткость принимается ряд основных гипотез и допущений:

1. 
   сплошность – материал не имеет в своей структуре пустот.
   
2. 
   однородность – одинаковые свойства материала в любой точке детали.
   
3. 
   изотропность – одинаковые свойства материала в различных направлениях.
   
4. 
   идеальная упругость (упругость – свойство тела восстанавливать форму и размеры после снятия нагрузки; пластичность – свойство тела получать большие остаточные деформации после снятия нагрузки).
   
5. 
   отсутствие первоначальных внутренних напряжений.
   
6. 
   принцип малых перемещений – перемещения конструкции малы по сравнению с размерами конструкции.
   
7. 
   линейная деформируемость материала – в зоне действия упругих деформаций зависимость между силой и приращением размера линейная.
   
8. 
   гипотеза плоских сечений – плоское до нагружения сечение остается плоским и после нагружения.
   

Все свойства физической модели, описанные уравнениями, составляют математическую модель деформированного тела. Математическая модель должна содержать три группы уравнений:

1. 
   статические - включающие нагрузки и условия равновесия;
   
2. 
   физические - отражающие связь между нагрузками и деформациями;
   
3. 
   геометрические - отражающие изменение формы и размеров под нагрузкой.
   

Геометрические характеристики сечения
Сопротивление стержня различным видам деформаций часто зависит не только от материала и размеров, но и от очертаний оси, формы поперечного сечения и их расположения относительно направления действующих нагрузок. Рассмотрим основные геометрические характеристики поперечных сечений стержня, отвлекаясь от физических свойств изучаемого объекта.

1. Площадь поперечного сечения. Данная величина может быть только положительной и имеет размерность [м²]:
F= . (1)
2. Статические моменты инерции. Данная величина может быть любого знака и имеет размерность [м³]:
S_х= , (2)

S_у= .
Оси, относительно которых статические моменты равны нулю, называются центральными. Точка пересечения центральных осей называется центром тяжести сечения.

3. Осевые моменты инерции. Данная величина может быть только положительной и имеет размерность [м⁴]:
I_х= , (3)

I_у= .
4. Центробежный момент инерции. Данная величина может быть любого знака и имеет размерность [м⁴]:

I_ху= . (4)
Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяжести, называются главными центральными осями.

5. Полярный момент инерции. Данная величина может быть только положительной и имеет размерность [м⁴]:
I_= = = I_х+ I_у (5)
6. Осевые моменты сопротивления. Данная величина может быть только положительной и имеет размерность [м³]:

W_х= , (6)

W_у= .
7. Полярный момент сопротивления. Данная величина может быть только положительной и имеет размерность [м³]:
W_= . (7)
8. Радиусы инерции. Данная величина имеет размерность [м]:
i_x= , (8)

i_у= .
Изменение геометрических характеристик при параллельном переносе координатных осей
Пусть известны геометрические характеристики сечения относительно осей ХY. Требуется определить геометрические характеристики сечения относительно осей Х₁Y₁. Известно, что оси этих двух систем координат параллельны (рис.10). Координаты любой точки в новой системе координат можно выразить через координаты в прежней системе координат следующим образом:
х₁ =х-а, (9)

у₁=у-b.



Рис.10
Запишем геометрические характеристики в новой системе координат по определению и сделаем замену «новых» координат на предыдущие:
S_х1= = = - = S_х – bF;

S_у1= = = - = S_y – aF;

I_х1= = = =

= - + = I_х-2bS_х + b²F; (10)

I_у1= = = =

= - + = I_y-2aS_y + a²F;

I_х1у1= = = =

= - - + = I_ху - aS_y – bS_x + abF.
Необходимо помнить, что координаты а и b, входящие в формулы, необходимо подставлять с учетом их знака.

Рассмотрим частный случай. Пусть оси Х₁Y₁ – центральные, тогда
S_х1= S_х - bF=0,

S_у1= S_у - аF=0.
Следовательно

b=S_х/F=у_с, (11)

a=S_y/F=х_с,

где х_с, у_с - координаты центра тяжести сечения в произвольной системе координат ХY.
Изменение геометрических характеристик при повороте координатных осей




Рис.11
Пусть известны геометрические характеристики сечения относительно осей ХY. Требуется определить геометрические характеристики сечения относительно осей Х₁Y₁. Известно, что оси этих двух систем координат повернуты друг относительно друга на угол  и имеют общее начало координат (рис.11). Координаты любой точки в новой системе координат можно выразить через координаты в прежней системе координат:
х₁=хcos+ysin, (12)

у₁=уcos-xsin.
Запишем геометрические характеристики в новой системе координат по определению и сделаем замену «новых» координат на предыдущие:
I_х1= = =

= =

= - + =

= I_хcos² - I_хуsin2 + I_уsin² ; (13)

I_у1= = =

= =

= + + =

= I_ycos² + I_хуsin2 + I_xsin² ;

I_х1у1= = =

= =

= - + -

- = I_хуcos² - 0,5I_ysin2 +0,5I_xsin2 - I_хуsin² =

= I_хуcos2 - 0,5sin2(I_y - I_x) .
Необходимо помнить, что угол , входящий в формулы, необходимо подставлять с учетом знака.

Сложим выражения для осевых моментов инерции при повороте координатных осей.
I_х1 + I_у1 = I_х(cos² + sin²) + I_у(sin² + cos² ) + I_ху(sin2- sin2) = I_х + I_у.
Отсюда можно сделать вывод, что при повороте координатных осей сумма осевых моментов инерции неизменна и равна полярному моменту инерции относительно начала координат.

Рассмотрим частный случай. Пусть оси Х₁Y₁ – главные центральные, тогда
I_х1у1= I_хуcos2 - 0,5sin2(I_y – I_x) = 0,

tg2 = . (14)
Необходимо помнить, что при решении задач угол, рассчитанный по формуле (14), откладывается против часовой стрелки, если он положителен и по часовой стрелке, если отрицателен.