Лекции по курсу сопротивление материалов
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
Пределом пропорциональности пц называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой и деформацией. Зона ОА называется зоной упругости. Здесь возникают только упругие, очень незначительные деформации. Данные, характеризующие эту зону, позволяют определить значение модуля упругости Е, как тангенс угла наклона этой прямой. После достижения предела пропорциональности деформации начинают расти быстрее, чем нагрузка, и диаграмма становится криволинейной. На этом участке в непосредственной близости от точки А находится точка В, соответствующая пределу упругости: уп= Пределом упругости уп называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации. У большинства металлов значения предела пропорциональности и предела упругости незначительно отличаются друг от друга. Поэтому обычно считают, что они практически совпадают. При дальнейшем нагружении криволинейная часть диаграммы переходит в почти горизонтальный участок СД – площадку текучести. Здесь деформации растут практически без увеличения нагрузки. Нагрузка Рт, соответствующая точке Д, используется при определении физического предела текучести: т= Пределом текучести т называется напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки. Предел текучести является одной из основных механических характеристик прочности металлов. Зона ВД называется зоной общей текучести. В этой зоне значительно развиваются пластические деформации. При этом происходит изменение внутренней структуры металла, что приводит к его упрочнению. Диаграмма после зоны текучести снова становится криволинейной, образец приобретает способность воспринимать возрастающее усилие до значения Рmax – точка Е на диаграмме. Это усилие используется для вычисления временного сопротивления или предела прочности: в= Пределом прочности называется напряжение, соответствующее максимальной нагрузке, достигнутой в ходе испытаний. Зона ДЕ называется зоной упрочнения. Здесь удлинение образца происходит равномерно по всей его длине, первоначальная цилиндрическая форма образца сохраняется, а поперечное сечение изменяется незначительно, но также равномерно. При максимальном или несколько меньшем усилии на образце в наиболее слабом месте возникает локальное уменьшение поперечного сечения – шейка. Дальнейшая деформация происходит в этой зоне образца. Сечение в середине шейки продолжает быстро уменьшаться, но напряжения в этом сечении все время растут, хотя растягивающее усилие и убывает. Вне области шейки напряжения уменьшаются, и поэтому удлинение остальной части образца не происходит. Наконец, в точке К образец разрушается. Сила, соответствующая точке К, называется разрушающей Рк, а напряжения – истинным сопротивлением разрыву: Sк= где Fк – площадь поперечного сечения в месте разрыва. Зона ЕК называется зоной местной текучести. Помимо указанных характеристик прочности определяют характеристики пластичности. Относительное удлинение после разрыва () – это отношение приращения расчетной длины образца после разрыва к ее первоначальному значению, вычисляемое по формуле: Заметим, что относительное удлинение после разрыва зависит от отношения расчетной длины образца к его диаметру. С увеличением этого отношения значение уменьшается, так как зона шейки (зона местной пластической деформации) у длинных образцов занимает относительно меньше места, чем в коротких образцах. Кроме того, относительное удлинение зависит и от места расположения шейки (разрыва) на расчетной длине образца. При возникновении шейки в средней части образца местные деформации в области шейки могут свободно развиваться и относительное удлинение будет больше, чем в случае, когда шейка возникает ближе к головке образца, тогда местные деформации будут стеснены. Другой характеристикой пластичности является относительное сужение после разрыва (), представляющее собой отношение уменьшения площади поперечного сечения образца в месте разрыва к начальной площади поперечного сечения образца: Диаграмма растяжения характеризует свойства образца, так как зависит от его размеров. Для оценки механических свойств материала диаграмму растяжения перестраивают в координатах «напряжение-деформация»: все ординаты делят на первоначальную площадь поперечного сечения F0, а все абсциссы – на первоначальную длину рабочей части l0. В результате получаем диаграмму напряжений, которая имеет тот же вид, что и диаграмма растяжения, так как F0 и l0 постоянны. Эта диаграмма является условной, поскольку при ее построении не учитывается изменение значений F0 и l0 в процессе испытания. Поэтому определенные ранее пределы пропорциональности, текучести и прочности являются условными. Истинные же напряжения в каждый момент нагружения будут больше условных. Заметное отклонение истинных напряжений от условных происходит после предела текучести, так как сужение сечения становится более значительным. Особенно сильно возрастает разница между напряжениями после образования шейки. Диаграмма напряжений, построенная с учетом сужения площади поперечного сечения и местного увеличения деформаций, называется диаграммой истинных напряжений. Некоторые диаграммы растяжения не имеют ярко выраженной площадки текучести, например, для низколегированных сталей, сплавов алюминия (рис.28). В этих случаях вместо физического предела текучести определяют условный предел текучести 0,2 (точка Д) – напряжение, при котором остаточное удлинение достигает 0,2 от рабочей длины образца. 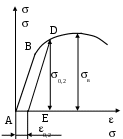 Рис.28 Математическая модель механики твердо деформируемого тела Полная математическая модель механики твердо деформированного тела состоит из трех частей: уравнения равновесия, геометрические соотношения и физические соотношения. Рассмотрим каждую из частей более подробно. I. Уравнения равновесия. В твердо деформированном теле выберем некоторую точку А с координатами (x,y,z). Вблизи этой точки вырежем объем dV=dxdydz. На каждой грани вырезанного элемента действует по три напряжения: одно нормальное и два касательных (рис.29). Кроме этого на элементарный объем действуют массовые силы R(X, Y, Z). 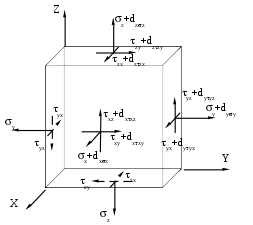 Рис.29 Так как все тело находится в равновесии, то в равновесии находится и элементарный объем и, следовательно, можно составить три уравнения равновесия сил в проекциях на оси координат. Напомним, что для того чтобы получить силу, необходимо умножить напряжение на площадь грани, на которой оно действует. -xdydz + (x + dxx)dydz - yxdxdz + (yx + dyyx)dxdz – - zxdxdy + (zx + dzzx)dxdy + Xdxdydz = 0, раскроем скобки и распишем частные производные поделим уравнение на элементарный объем Аналогично запишем уравнения равновесия по двум другим осям координат: Полученная система уравнений содержит шесть неизвестных компонентов: три нормальных напряжения и три касательных напряжения (с учетом закона парности касательных напряжений). Следовательно, этих уравнений недостаточно для решения поставленной задачи. II. Геометрические соотношения. В теле выберем некоторую точку А с координатами (x,y,z). После нагружения и деформации (рис.30) точка А переместилась в точку А1 с координатами (х1, у1, z1) на малую величину r (х, у, z). Введем обозначения х = х1 – х = U, у = у1 – у = V, (56) z = z1 – z = W, где U, V, W – перемещения вдоль координатных осей Х, У, Z. Теперь возьмем отрезок АВ бесконечно малой длины dS с направляющими косинусами (l, m, n). Изменение длины отрезка под нагрузкой dS1 - dS = dS называется абсолютным удлинением или приращением. 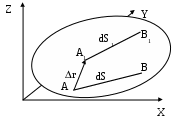   Рис.30 Отношение приращения к первоначальной длине отрезка называется относительным удлинением или линейной деформацией: = Пусть отрезок dS имеет проекции по координатным осям (dx, dy, dz). Зная направляющие косинусы отрезка, найдем величину проекций: dx=ldS, dy=mdS, (58) dz=ndS. Найдем длину отрезка dS через проекции: dS2 = dx2 + dy2 + dz2. Продифференцируем это выражение: 2dSdS = 2dxdx + 2dydy + 2dzdz (59) учитывая выражения (56), можно записать: dx = dx =dU, dy = dy = dV, (60) dz = dz = dW. Подставим полученные выражения в (59): dSdS = dxdU + dydV + dzdW, следовательно, приращение отрезка равно: dS = найдем линейную деформацию по формуле (57) с учетом выражения (61): = Перемещения U, V, W являются функциями трех координат, так как они зависят от положения точки в теле по отношению к опорам и приложенным нагрузкам. Следовательно, полный дифференциал является суммой частных производных. Поделим каждое из уравнений (63) на dS: Подставим полученные выражения (64) в уравнение деформации (62): Раскрыв скобки и сгруппировав слагаемые по направляющим косинусам, получим полное выражение для линейной деформации: Введем обозначения Эти выражения получили название формул Коши. Они связывают между собой компоненты тензора деформаций и перемещения точки. С учетом формул Коши деформация в произвольном направлении получит следующий вид: Определим физический смысл введенных обозначений. Формула (66) справедлива для любого направления, поэтому возьмем отрезок dS параллельно оси Х, тогда его длина определяется проекцией на эту ось dS=dx и направляющие косинусы равны l=1, m=n=0. Согласно уравнению (66) деформация отрезка в этом случае будет равна: = т.о. х – линейная деформация в направлении оси Х; аналогично у – линейная деформация в направлении оси Y; z – линейная деформация в направлении оси Z. Теперь определим, что такое . Возьмем в теле прямой угол АВС со сторонами, параллельными осям координат. После нагружения тела, угол деформировался и занял положение А1В1С1 (рис.31). 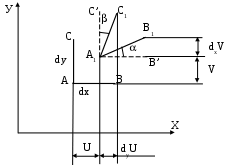 Рис.31 Точка А переместилась вдоль оси Y на V, а точка В вдоль той же оси переместилась на V+dxV. При этом длина отрезка dx стала dx+dx. Рассмотрим треугольник А1В1В’: tg = Аналогично рассмотрим треугольник А1С1С’: tg = Первоначально прямой угол уменьшился на +. С учетом того, что при малых углах tg получаем: Таким образом, получается, что ху – изменение прямого угла со сторонами, параллельными координатным осям, т.е. угловая деформация в плоскости ХY. Аналогично можно получить две других угловых деформации. III. Физические соотношения. При испытаниях на растяжение был экспериментально установлен закон Гука: Также опытным путем установлены модуль Юнга Е – коэффициент пропорциональности между нормальным напряжением и линейной деформацией и коэффициент Пуассона – отношение поперечной деформации к продольной. Рассмотрим закон Гука в главных осях. 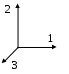  Рис.32 При одноосном напряженном состоянии (рис.32) деформации по трем осям будут равны: П 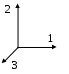 ри рассмотрении трехосного напряженного состояния (рис.33) воспользуемся принципом суперпозиции, т.е. найдем деформации по осям от каждого напряжения в отдельности. ри рассмотрении трехосного напряженного состояния (рис.33) воспользуемся принципом суперпозиции, т.е. найдем деформации по осям от каждого напряжения в отдельности.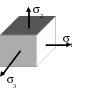 Рис.33 От напряжения 1: От напряжения 2: От напряжения 3: Найдем суммарные деформации по координатным осям. Формулы (71) представляют собой закон Гука в главных осях. Эти формулы связывают главные напряжения и главные деформации. Вне главных осей существуют касательные напряжения и искажение углов. Следовательно, существует связь между ними. Для установления этой связи перейдем от главных осей к произвольным: Нормальное напряжение 1 можно выразить по основной квадратичной форме (33) через напряжения в произвольных осях: 1 = xl2 + ym2 +zn2 + 2yxml + 2zxnl + 2zynm Подставим это выражение в формулу (72) и умножим первый инвариант на сумму квадратов направляющих косинусов (l2 + m2 + n2 = 1) 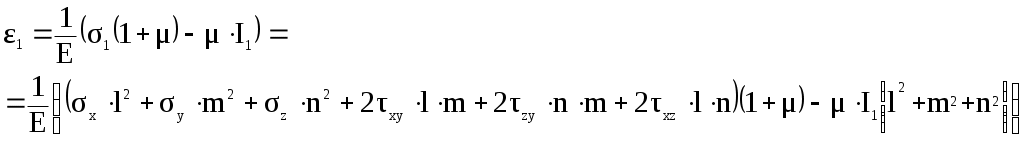 Раскроем скобки и сгруппируем слагаемые по направляющим косинусам: 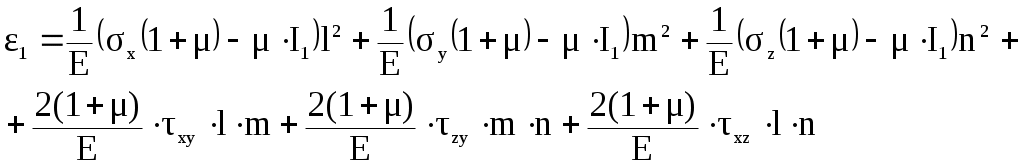 Сравним полученное выражение с квадратичной формой деформации в произвольном направлении (66): Где G= Уравнения (73) являются обобщенным законом Гука, выражающим связь между напряжениями и деформациями. Таким образом, рассмотрев три части математической модели, мы имеем 15 уравнений (3 уравнения равновесия, 6 формул Коши, 6 уравнений обобщенного закона Гука) и 15 неизвестных (3 перемещения по координатным осям, 3 нормальных напряжения, 3 касательных напряжения, 3 линейных деформации, 3 угловых деформации). Построение математической модели механики твердо деформированного тела – предмет изучения линейной теории упругости. Полученная математическая модель не является ещё полной, так как часть уравнений (формулы Коши и уравнения равновесия) имеют дифференциальный вид. Их нужно интегрировать. В результате чего появляются постоянные интегрирования, то есть дополнительные неизвестные. В обыкновенных дифференциальных уравнениях это константы, для уравнений в частных производных это функции. Поэтому необходимо существование дополнительных условий. Это так называемые граничные условия – условия на границе данного тела (на поверхности). Граничные условия бывают трех типов: силовые, геометрические и смешанные. |
