Лекции по курсу сопротивление материалов

• Название: Лекции по курсу сопротивление материалов
• Дата: 29.11.2021
• Размер: 1.05 Mb.
• Имя файла: LEKTsII_PO_SM-1s.doc
• Тип: Лекции; #285343
• страница: 5 из 7

Деформированное состояние тела
Выделим в теле прямоугольный параллепипед. После нагружения он трансформируется в косоугольный, то есть появляются линейные и угловые деформации. Деформированное состояние характеризуется тензором деформаций. Этот тензор будет симметричным, так как _ху = _ух (угловые деформации одного и того же прямого угла).

Сравним основные квадратичные формы для нормального напряжения и линейной деформации:
_ = _xl² + _ym² +_zn² + 2_yxml + 2_zxnl + 2_zynm


Как видно, формулы полностью аналогичны. Коэффициенты при направляющих косинусах являются составляющими тензора деформаций: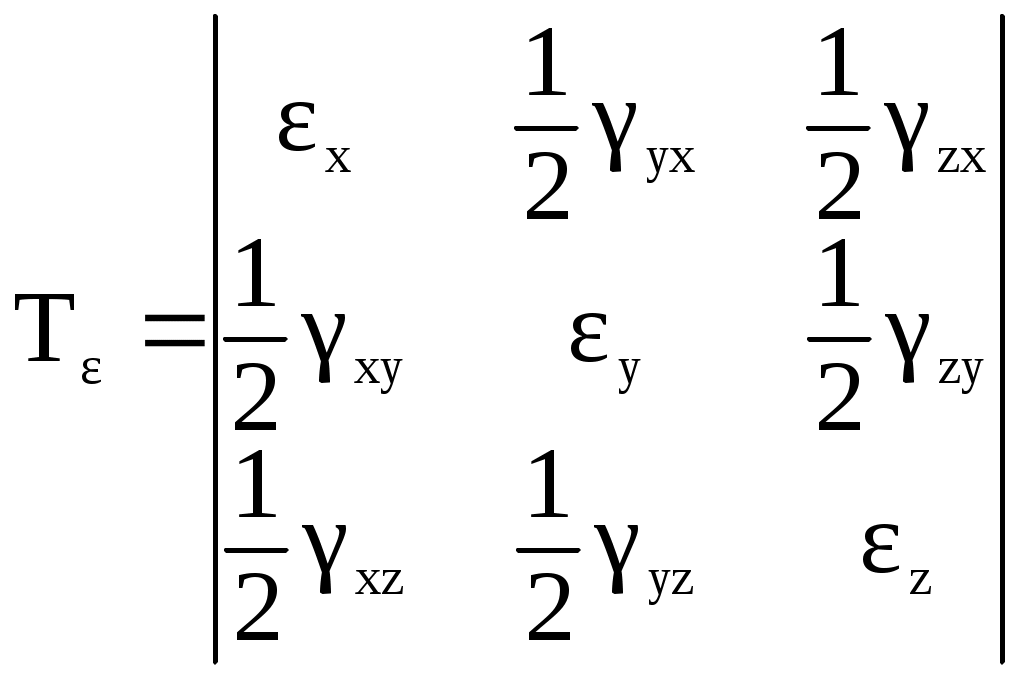
(74)
Также существуют инварианты деформированного состояния, которые определяются аналогично инвариантам напряженного состояния:
₁ = _х + _у + _z,

₂ = _х_у + _у_z + _z_х - , (75)

₃ = Т_.
Для определения величины главных деформаций существует основное характеристическое уравнение деформированного состояния:
³ - ₁² + ₂ - ₃ = 0
Корни данного уравнения нумеруются в порядке убывания: ₁  ₂  ₃. Главные деформации - это линейные деформации в направлении, перпендикулярном главным площадкам деформации, а главными площадками деформации являются такие, в которых угловые деформации равны нулю. Главные площадки расположены по трем взаимно перпендикулярным осям, которые называются главными осями деформированного состояния.
Касательные напряжения при кручении
Задачу по определению касательного напряжения при кручении будем решать с использованием двух гипотез:

- гипотеза плоских сечений;

- радиус, проведенный в сечении до деформации, не искривляется в процессе деформации.

Рассмотрим стержень, нагруженный крутящим моментом. На некотором расстоянии z от начала стержня вырежем бесконечно малый элемент dz (рис.34).





Рис.34
Рассмотрим статическую сторону задачи. Для этого найдем связь между крутящим моментом в сечении (рис.35) и касательным напряжением. Любой момент - это произведение силы на плечо. В данном случае для элементарного крутящего момента сила - это произведение касательного напряжения на площадь, на которой оно действует, а плечо есть радиус-вектор от центра тяжести сечения до рассматриваемой точки.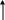









Рис.35
М_к = (76)
Теперь рассмотрим вырезанный элемент dz (рис.36) с геометрической стороны. В процессе нагружения правое сечение повернется по отношению к левому на некоторый угол dφ. Отрезок АВ после деформации занял положение АВ₁.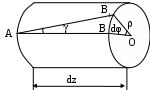



Рис.36
Найдем длину дуги ВВ₁ из треугольников АВВ₁ и ОВВ₁:
dz = dφ

(77)
С физической точки зрения при сдвиге справедлив закон Гука.
 = G (78)
Подставим угловую деформацию из геометрического соотношения (77) в закон Гука (78):
 = G (79)
Полученное выражение подставим в формулу (76):
М_к = ,

= .
сделав подстановку в выражение (77), получим:
,
полученное выражение подставляем в закон Гука (78):
 = G.
Окончательно получаем формулу для расчета касательных напряжений в сечении при кручении:
 = (80)
Таким образом, касательные напряжения при кручении круглого стержня распределяются по линейному закону и достигают своего максимума на периферии сечения.
Касательные напряжения при изгибе. Формула Журавского
Рассмотрим задачу об определении касательных напряжений при изгибе для узкого прямоугольника в качестве сечения.

При изгибе Q_у 0 и М_х 0. В этом случае в сечении возникают три напряжения _z, _zx, _zy. Тогда уравнения равновесия (54) и (55) из полной математической модели твердо деформированного тела примут следующий вид:


,

.
Из первых двух уравнений следует, что касательные напряжения являются функцией двух переменных (х, у). так как поверхность стержня свободна от напряжений, то по периметру сечения _zx = 0 по закону парности касательных напряжений (рис.37).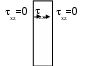

Рис.37
Для узкого прямоугольника они не успевают вырасти, поэтому будем считать _zx равными нулю по всей ширине сечения. Тогда третье уравнение равновесия примет вид:

. (81)
По той же причине, что прямоугольник узкий, будем считать, что _zy по ширине сечения при у = const распределено равномерно и является функцией только координаты у:
.
Пользуясь формулой нормальных напряжений в поперечном сечении (28), при изгибе получим:
 = ,

= ,

М_х’ = Q_y

.
Проинтегрировав полученное выражение, получим:
_zy=-  . (82)
Постоянную интегрирования можно определить из условия равенства нулю касательного напряжения _zy при у= :
=0,

С = - .
Подставив значение константы в выражение (82) получим:
_zy=- 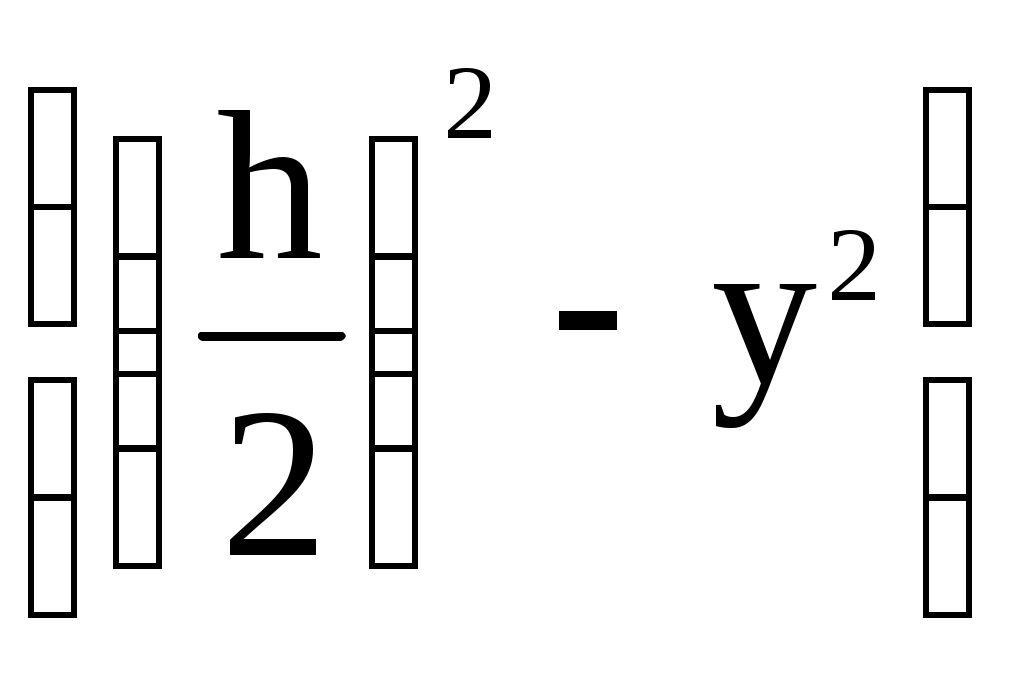 =  . (83)
На основе выражения в скобках можно сделать вывод, что касательные напряжения в сечении распределены по параболе.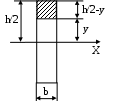



Рис.38
Преобразуем выражение в скобках: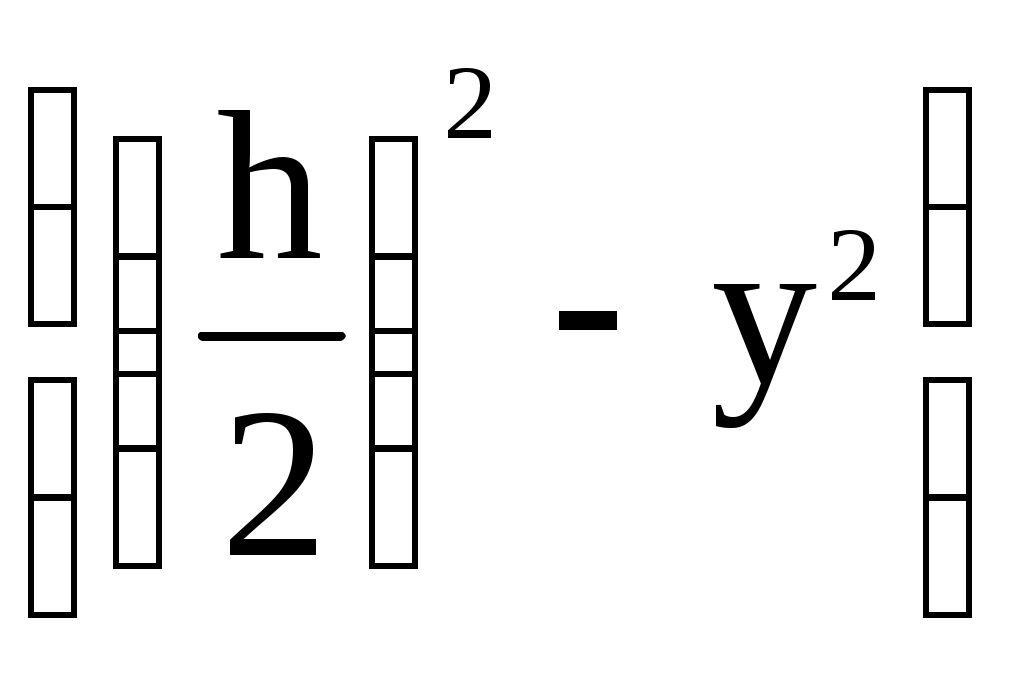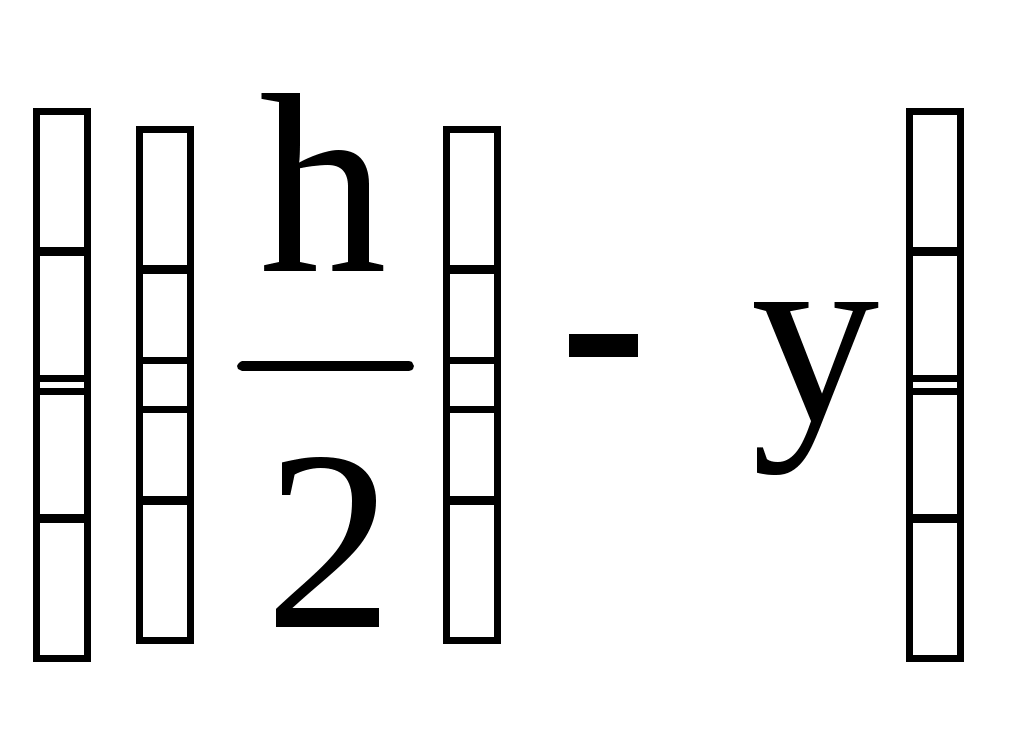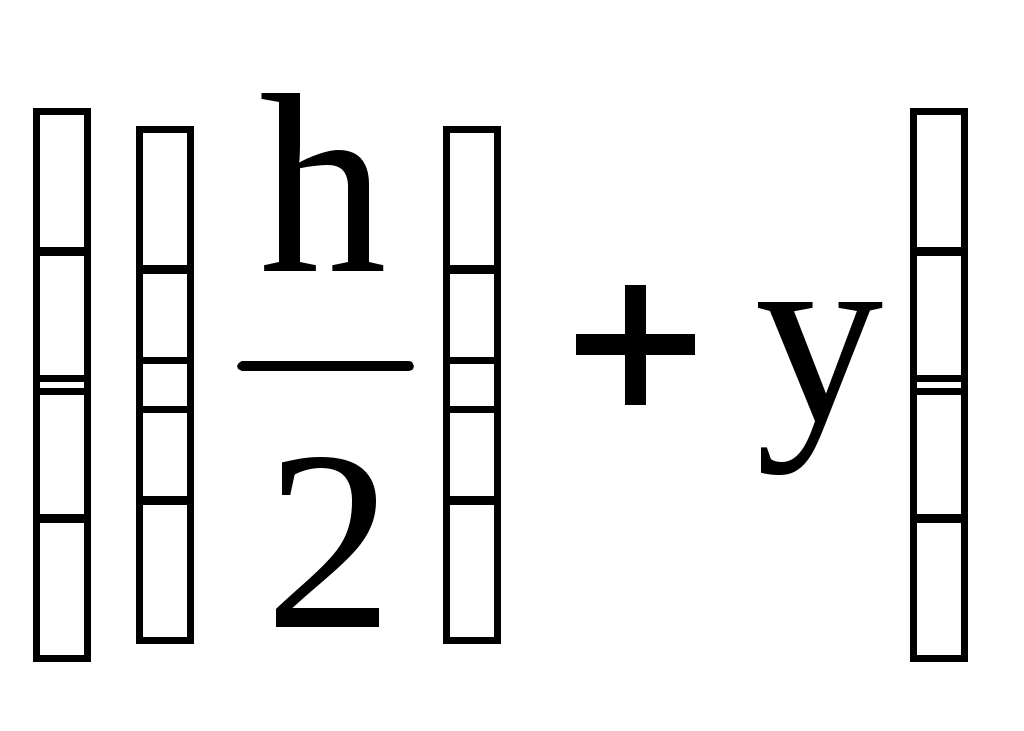
 =  
На рисунке 38 координатой y отсекается заштрихованная часть, которая имеет площадь F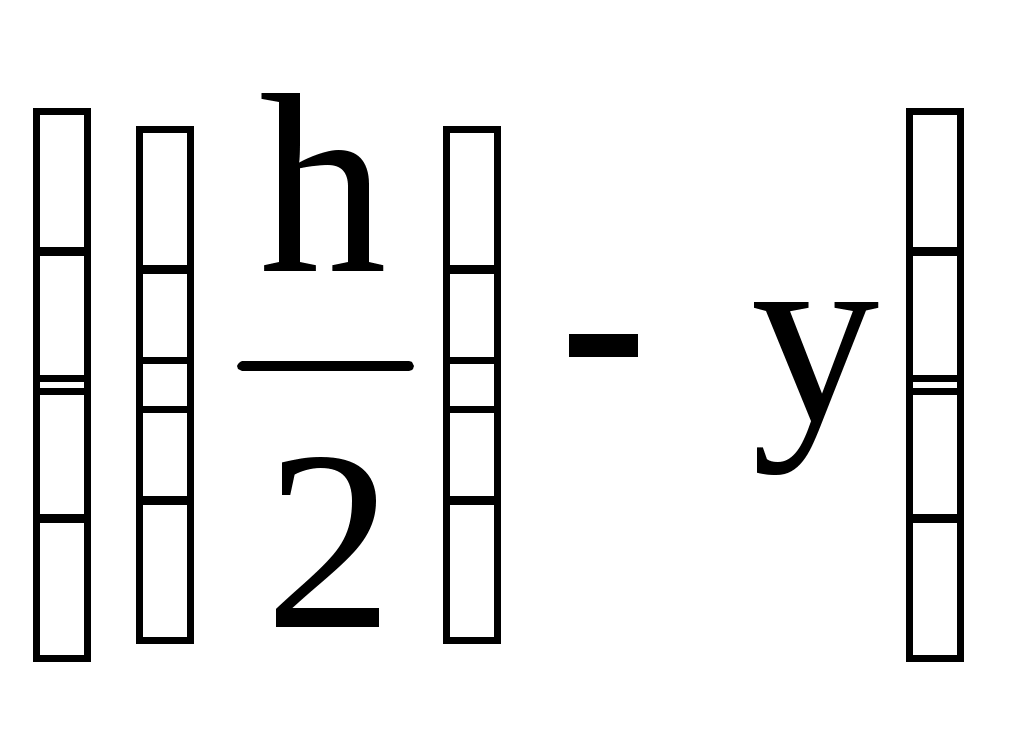^*= b и координату центра тяжести относительно оси х у_с^*=  . Произведение площади фигуры на координату ее центра тяжести относительно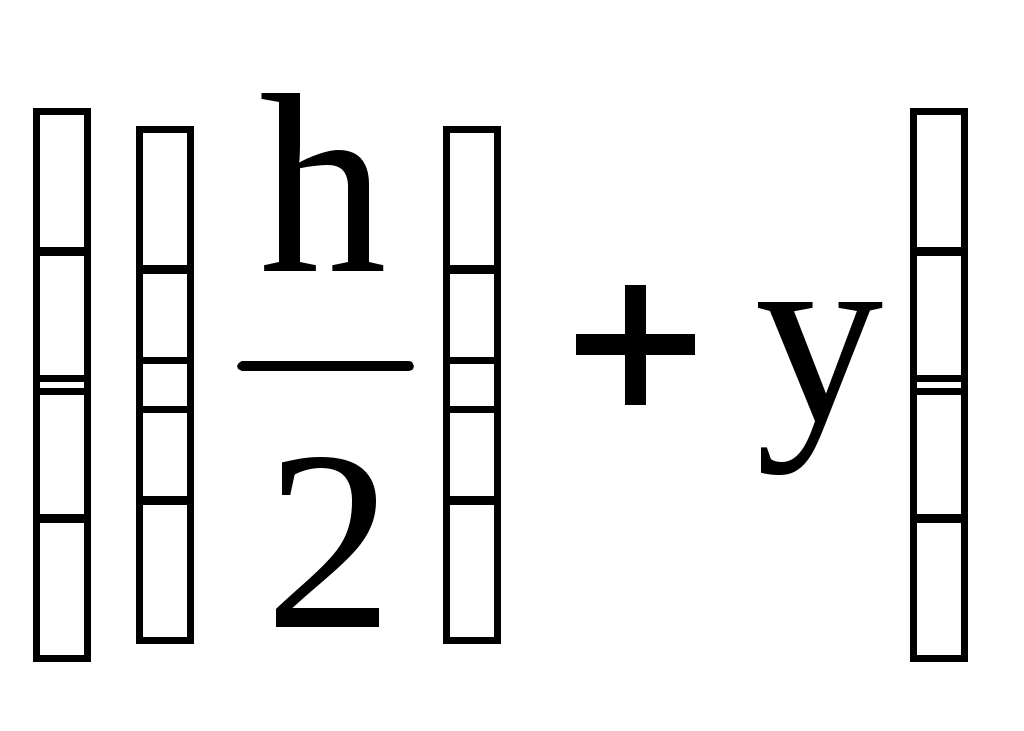 какой-либо оси дает статический момент инерции S_x^*. Таким образом, выражение (83) примет вид:
_zy= (84)

Эта формула носит название формулы Журавского и служит для определения касательных напряжений, возникающих в сечении при изгибе.
Теории (гипотезы) прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию, т.е. по известным главным напряжениям в каждой точке тела.

Наиболее просто эта задача решается при простых видах деформации, в частности, при одноосных напряженных состояниях, так как в этом случае экспериментально легко установить значение предельных (опасных) напряжений. Под последними понимают напряжения, соответствующие началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластического состояния материала).

Так, испытания образцов из определённого материала на простое растяжение или сжатие позволяют без особых трудностей определить значение опасных напряжений: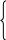
_т – предел текучести

_о =

_в – временное сопротивление.
По опасным напряжениям устанавливают допускаемые при растяжении [₊] или сжатии [_-] напряжения, обеспечивая коэффициент запаса против наступления предельного состояния.

Таким образом, условие прочности при одноосном напряженном состоянии принимает вид:
₁[₊],

|₃| [₊].
Рассмотрим теперь вопрос о прочности материала при сложном напряженном состоянии, когда в точках детали два или все три главных напряжения ₁, ₂, ₃ не равны нулю.

В этих случаях, как показывают опыты, для одного и того же материала опасное состояние может иметь место при различных предельных значениях главных напряжений в зависимости от соотношений между ними. Поэтому экспериментально установить предельные величины главных напряжений очень сложно не только из-за трудности постановки опытов, но и из-за большого объема испытаний.

Другой путь решения задачи заключается в установлении критерия прочности (критерия предельного напряженно-деформированного состояния). Для этого вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора: полагают, что нарушение прочности материала при любом напряженном состоянии наступит только тогда, когда величина данного фактора достигнет некоторого предельного значения. Предельное значение фактора, определяющего прочность, находят на основании простых, легко осуществимых опытов на растяжение. Иногда пользуются также результатами опытов на кручение. Таким образом, введение критерия прочности позволяет сопоставлять данное сложное напряженное состояние с простым, например, с одноосным растяжением, и установить при этом такое эквивалентное (расчётное) напряжение, которое в обоих случаях дает одинаковый коэффициент запаса.

Под коэффициентом запаса в общем случае напряженного состояния понимают число n, показывающее, во сколько раз нужно одновременно увеличить все компоненты напряженного состояния ₁, ₂, ₃, чтобы оно стало предельным.

В настоящее время разработано достаточно большое число гипотез прочности. Ниже рассмотрим некоторые из них.

Первая теория прочности (теория наибольших нормальных напряжений).

Согласно этой теории, выдвинутой Галилеем (XVII в.), преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения.

Нарушение прочности в общем случае напряженного состоянии наступает тогда, когда наибольшее нормальное напряжение достигает опасного значения (₀). Последнее легко устанавливается при простом растяжении на образцах из определённого материала.

Условие нарушения прочности при сложном напряженном состоянии имеет вид
₁=₀.
Следовательно, условие прочности с учетом коэффициента запаса n будет
₁[], (85)

где

[]= .
Таким образом, первая теория прочности из трех главных напряжений учитывает лишь одно – наибольшее, полагая, что два других не влияют на прочность.

Опытная проверка показывает, что эта теория прочности непригодна для большинства материалов и дает, в общем, удовлетворительные результаты лишь для весьма хрупких материалов.

Вторая теория прочности (теория наибольших линейных деформаций).

Согласно второй теории прочности, предложенной Мариоттом (1682г.), принимается в качестве критерия прочности наибольшая по абсолютной величине линейная деформация. По этой теории нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая линейная деформация _max достигает своего опасного значения ₀. Последнее определяется при простом растяжении образцов из определённого материала.

Таким образом, условия разрушения и прочности соответственно будут:
_max=₀,

_max[]= . (86)
Используя обобщенный закон Гука, легко выразить условие прочности в напряжениях:
_max=₁= [₁-(₂+₃)].
При простом растяжении, приняв в качестве допускаемого напряжения [], мы тем самым для наибольшего относительного удлинения допускаем величину
[]= .
Подставляем выражения для _max и [] в (86) и находим:
[₁-(₂+₃)]  []. (87)
Опытная проверка этой теории также показала, что она неприменима для большинства материалов и дает удовлетворительные результаты лишь для хрупкого состояния материала (например, легированный чугун, высокопрочные стали после низкого отпуска). Отметим также, что применение второй теории прочности в виде (87) недопустимо для материалов, не подчиняющихся закону Гука, или за пределами пропорциональности, а также когда наибольшая по абсолютной величине деформация отрицательна.

Третья теория прочности (теория наибольших касательных напряжений).

Согласно третьей теории прочности, предложенной Кулоном (1773 г.), в качестве критерия прочности принимается величина наибольшего касательного напряжения. По этой теории нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшее касательное напряжение _max достигает своего предельного значения ₀. Последнее определяется в момент разрушения при простом растяжении.

Условия разрушения и прочности имеют вид
_max=₀,

_max[]= . (88)
Так как согласно круговой диаграмме Мора
_max = ,

₀ = ,
то условия разрушения и прочности (88) можно выразить через главные напряжения:
₁-₃ = ₀,

₁-₃  []. (89)
Третья теория прочности, в общем, хорошо подтверждается опытами для пластичных материалов, одинаково работающих на растяжение и сжатие. Для хрупких материалов она неприменима.

Недостаток третьей теории заключается в том, что она не учитывает среднего по величине главного напряжения ₂, которое, как показывают опыты, оказывает также некоторое влияние на прочность материала.