Лекция № 8. Лекция Статистические гипотезы

• Название: Лекция Статистические гипотезы
• Дата: 05.06.2022
• Размер: 283.14 Kb.
• Имя файла: Лекция № 8.docx
• Тип: Лекция; #570505
• страница: 3 из 3

1в. В случае, если проверяется действие фактора на качественный признак, то чаще используется проверка соотношения долей и критерий χ² .

Пример 6. В группе из 100 детей дошкольного возраста, вакцинированных против гриппа, во время эпидемии заболели 30. В другой группе детей из 100 детей, не вакцинированных, заболели 70. Определить, достоверны ли эти различия.

В качестве нулевой гипотезы принимается предложение о том, что средние двух выборок равны между собой. Кроме того, определяется ожидаемое значение результата, в качестве которого обычно берется средний результат. Так, для нашего примера, среднее составляет (70+30)/2=50.

Вводим в любую свободную ячейку рабочего листа, например, в А1 значение 70, в В1 – 30, в А2 и В2 – 50. Выделяем ячейку С1(или любую свободную), входим в меню Вставка/Функция/Статистические и выбираем функцию ХИ2ТЕСТ. В поле Фактический интервал указываем A1:B1, в поле Ожидаемый интервал – А2:В2 и в заключение следует щелкнуть кнопку ОК. Если получившееся значение больше заданного уровня значимости, то нулевая гипотеза сохраняется.

Для нашего примера полученное значение составляет 0,0000633. Поскольку оно значительно меньше уровня значимости, принимаемого нами равным 0.05, то нулевая гипотеза отвергается, таким образом в нашем случае оказалось, что вакцинация действительно является эффективной.

Пример 7. Изучалась заболеваемость ОРВИ в течение месяца на нескольких участках поликлиники. Данные приведены в табл. 9. Следует отметить, что поскольку заболеваемость измеряется относительно количества населения, то оно предполагается одинаковым на всех участках.

Табл. 9

Участок	Число обращений	Р-Р’	(P-P’)2	(P-P’)2/P’
1	17	1	1	0.06
2	15	1	1	0.06
3	18	2	4	0.25
4	14	2	4	0.25
5	16	0	0	0
Всего	80			0.63

Если предположить, что заболеваемость одинакова на всех участках, то ожидаемое число случаев Р’ составит 80/5=16 случаев. Заполним третий-пятый столбцы таблицы по приведенным формулам, в результате получим значение 0.63. Табличное значение для критерия χ² (приложение 10) при числе степеней свободы 5-1=4 составляет 9.48. Поскольку вычисленное значение значительно меньше табличного, то нулевая гипотеза остается в силе, т.е. заболеваемость одинакова на всех представленных участках.

Пример 8. Оценить различия уровня заболеваемости в различных возрастных группах. Исходные данные и расчеты приведены в табл. 10.

Табл. 10

	Возраст (лет)
	До 30	30-39	40-49	50 и более	Всего
Число сотрудников	55	60	120	47	282
Случаев заболевания	11	17	33	6	67
Частота заболевания,%	20	28.3	27.5	12.8	23.8
Ожидаемые случаи (Р’)	13	14	29	11	70
(Р-Р’)	2	3	4	5
(P-P’)2	4	9	16	25
(P-P’)2/P’	0.327	0.528	0.707	2.391	3.953

Если заболеваемость во всех возрастных группах предполагается одинаковой, то она составит 67/282*100=23.8%. Вычислим ожидаемый процент заболеваемости в каждой возрастной группе:

55*0.238=13, 60*0.238=14, 120*0.238=29, 47*0.238=11.

Суммируя элементы последней строки, получим 3.953. Полученное число сравнивают с табличным значением критерия для числа степеней свободы, равного 4-1=3, где 4 – количество категорий. Табличное значение составляет 9.2. Следовательно, нулевая гипотеза сохраняется, таким образом, заболеваемость одинакова для всех возрастных групп.

Для оценки показателей структуры заболеваемости используется методика применения χ², предложенная В.Ю.Урбахом и модифицированная коллективом авторов (Л. Е. Поляков, Д. М. Малинский, М. В. Дубовик). Данная методика используется для сравнения двух рядов данных о заболеваемости. Для вычислений используется формула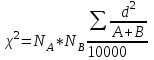

, (10)

где N_A и N_B – итоговые числа для групп А и В, A+B – суммарное число случаев заболевания.

Пример 9. Пусть данные о структуре заболеваемости для двух населенных пунктов представлены в табл. 11.

Табл.11

заболевания	Случаев заболеваний					d=A-B%	d2	d2/(A+В)
	А	В	А+В	А%	В%
Инфекционные	28	43	71	19,6	30,3	10,7	114,49	1,613
Органов дыхания	45	32	77	31,5	22,5	9	81	1,052
Органов пищеварения	31	33	64	21,7	23,2	1,5	2,25	0,035
Мочеполовых органов	17	10	27	11,9	7	4,9	24,01	0,888
Прочие	22	24	46	15,4	16,9	1,5	2,25	0,049
Всего	143	142						3,637

Показатель А% вычисляется как отношение соответствующего значения показателя А к общему количеству случаев заболеваний. Так, для инфекционных заболеваний показатель А% равен 28/143*100%=19.58≈19.6. Подставляя в формулу (45) вычисленные значения, получаем χ² =143*142*3.637/10000=7.38. Поскольку фактическое значение критерия меньше критического для числа степеней свободы k=5-1=4, равного 9.45, то нулевая гипотеза сохраняется, таким образом структура заболеваемости одинакова.

Другой способ сравнения выборочных долей: нужно вычислить отношение разности долей к своей ошибке и полученную величину сравнить с критерием Стьюдента для принятого уровня значимости и числа степеней свободы k=n₁+n₂-2. Если полученное значение больше табличного, то нулевая гипотеза отклоняется.

Ошибка разности между долями вычисляется по формулам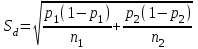

(11)

для равновеликих выборок или, если объем одной из выборок больше объема другой не больше, чем на 25%.

, (12)

если при тех же условиях доли выражены в процентах от общего числа наблюдений.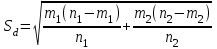

, (13)

если численности сопоставляемых групп выражены в абсолютных числах.

Если же численность одной группы превосходит численность другой более, чем на 25%, то формула ошибки имеет вид: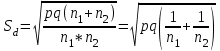

, (14)

где n₁ и n₂ – численности групп, на которых определяются доли pи q, причем p определяется как средняя взвешенная из p₁ и p₂ долей или из абсолютных численностей групп: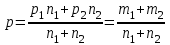

, (15)

где q=1-p, а если доли выражены в процентах от n, то q=100-p.

Пример 10. Из 23 пациентов, составивших одну группу больных пневмонией, возраст которых не превышал 35 лет, у 14 человек к концу 1-х суток наблюдалась положительная динамика (снижение температуры), у 9 – не наблюдалось. Из 20 больных в возрасте превышавшем 35 лет – соответственно 12 и 8. Разница между количеством пациентов с положительной динамикой в двух группах составляет 2. Ошибка разности, вычисленная по формуле (47) составляет 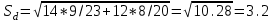, t_факт=2/3.2≈0.62.

Для k=20+23-2=41 и 5% уровня значимости находим t=1.96. Таким образом, нулевая гипотеза остается в силе, т.е. влияние возраста на скорость положительной динамики остается недоказанной.

Особый интерес представляет случай, когда доля составляет 0% или 100%. В этом случае для вычисления ошибки используется величина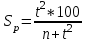

(16)

где величина t определяется в соответствии с уровнем вероятности следующим образом: для p=0.95 t=1.96, для p=0.99 t=2.58, для p=0.999 t=3.29.

Пример 11. В группе из 35 вакцинированных детей поствакциональные осложнения не были отмечены ни у одного ребенка. Означает ли это, что вакцина абсолютно безопасна? Каков может быть ожидаемый процент поствакциональных осложнений во всей совокупности ?

Для нашего примера при уровне вероятности p=0.95 получим 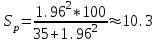. Таким образом, реальная доля поствакциональных осложнений составит 10.3%, соответственно, вероятность благоприятного течения поствакционального периода составит 100-10.3=89.7 %.