Лекция № 8. Лекция Статистические гипотезы
 Скачать 283.14 Kb. Скачать 283.14 Kb.
|
|
Лекция № 8. Статистические гипотезы Решение той или иной задачи, как правило, не обходится без сравнений. Сравнивать приходится данные опыта с контролем, группы больных с разным характером заболевания, воздействие двух и более видов препаратов в различных формах и т.д. О преимуществе одной из сравниваемых групп судят обычно по разности между выборочными средними. Но так как выборочные показатели — величины случайные, варьирующие вокруг своих генеральных параметров, которые в подавляющем большинстве случаев остаются неизвестными, то и разность между этими показателями может возникнуть не вследствие систематически действующих на признак, а чисто случайных причин. Чтобы решить вопрос об истинной значимости различий, наблюдаемых между выборочными средними, исходят из статистических гипотез — предположений или допущений о неизвестных генеральных параметрах, выражаемых в терминах вероятности, которые могут быть проверены на основании выборочных показателей. В области биометрии применяется обыкновенно так называемая нулевая гипотеза (Н0), т. е. предположение о том, что между генеральными параметрами сравниваемых групп разница равна нулю и различия, наблюдаемые между выборочными показателями, носят не систематический, а исключительно случайный характер. Так, если одна выборка взята из совокупности с параметрами μ1 и σ1 а другая—из совокупности, характеризуемой параметрами μ2 и σ2, то нулевая гипотеза предполагает, что μ1 – μ2 = 0. Противоположная, или альтернативная (Н1), гипотеза, наоборот, исходит из предположения, что μ1 – μ2 ≠ 0. Истинность принятой гипотезы проверяется с помощью критериев значимости, или достоверности, т. е. специально выработанных случайных величин, функции распределения которых известны. Обычно для каждого критерия составляется таблица, в которой содержатся критические точки, отвечающие определенным числам степеней свободы (k) и принятым уровням значимости (α). Уровень значимости — значение вероятности, при котором различия, наблюдаемые между выборочными показателями, можно считать несущественными, случайными. В исследовательской работе обычно принимается 5%-ный уровень значимости, которому отвечают вероятность Р=0.95и нормированное отклонение t=1.96, если распределение критерия нормально. В более ответственных случаях применяется 1%-ный уровень значимости, которому соответствуют Р = 0.99 и t = 2.58 для нормального распределения критерия, или еще более высокий 0.1%-ный уровень значимости, которому отвечают Р=0.999 и t = 3.29. Критерии значимости делятся на параметрические и непараметрические. Первые строятся на основе параметров выборочной совокупности и представляют функции этих параметров, вторые — функции от вариант данной совокупности с их частотами. Параметрические критерии применимы лишь в тех случаях, когда генеральная совокупность, из которой взята выборка, распределяется нормально, и при условии, что генеральные параметры сравниваемых групп равны между собой, т. е. 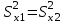 и и 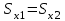 . Непараметрические критерии таких ограничений не имеют, они применимы к распределениям самых различных форм. Параметрические критерии связаны с необходимостью вычисления выборочных характеристик— средней величины и показателей вариации. При использовании непараметрических критериев такая необходимость отпадает. Параметрические критерии обладают большей мощностью по сравнению с критериями непараметрическими, поэтому во всех случаях, когда исследуемая совокупность распределяется по нормальному закону или не очень сильно отклоняется от него, следует отдавать предпочтение критериям параметрическим. . Непараметрические критерии таких ограничений не имеют, они применимы к распределениям самых различных форм. Параметрические критерии связаны с необходимостью вычисления выборочных характеристик— средней величины и показателей вариации. При использовании непараметрических критериев такая необходимость отпадает. Параметрические критерии обладают большей мощностью по сравнению с критериями непараметрическими, поэтому во всех случаях, когда исследуемая совокупность распределяется по нормальному закону или не очень сильно отклоняется от него, следует отдавать предпочтение критериям параметрическим.Итак, одной из основных задач биометрии является проверка достоверности различий двух выборочных средних. В свою очередь, в этой задаче можно выделить отдельные типы задач. Следует прежде всего отметить, что выборки до эксперимента должны быть сопоставимы во всех отношениях, т.е. должны иметь одинаковую возрастно-половую структуру, состояние здоровья и т.д. Для повышения репрезентативности результатов объекты в выборки должны выбираться случайным образом. Далее одна из выборок (опытная) подвергается воздействию, а вторая (контрольная) – нет. 1а. Сравнение двух альтернативных выборок, в которых изучаемый признак имеет числовое выражение, например, двух групп пациентов с применением соответственно различных методик лечения; в качестве исследуемого признака может выступать среднее значение какого-либо биохимического показателя, среднее время, затраченное на лечение одного пациента, и т.д. Для решения задачи о значимости разницы выборочных средних используются как параметрические, так и непараметрические критерии. Наиболее часто исследователи используют критерий Стьюдента, при этом часто игнорируется основное требование к его применению – соответствие выборочных данных нормальному (Гауссову) закону распределения. Таким образом, применение критерия Стьюдента должно быть не первым, а вторым этапом оценивания результатов. На первом же этапе следует проверить соответствие имеющегося закона распределения нормальному закону (см. ниже). Предположим, что соответствие распределения случайной величины нормальному закону распределения доказано. В этом случае процедура применения критерия Стьюдента выглядит следующим образом: вычисляется величина tфакт в соответствии с формулой: 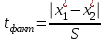 (1) (1)где величина S называется ошибкой разности средних и вычисляется по формуле 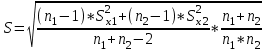 (2) (2)в случае выборок различного объема или по формуле 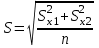 (3) (3)в случае выборок одинакового объема и в случае, если генеральные дисперсии сравниваемых совокупностей одинаковы. Если же генеральные дисперсии различны, то для вычисления ошибки средних используется формула 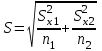 (4) (4)В этих формулах значение величины tфакт сравнивается с табличным значением критерия Стьюдента для требуемого уровня вероятности и числа степеней свободы k, определяемого как n1+n2-2, где n1 и n2 – объемы выборок в случае одинаковых дисперсий. Если же дисперсии различны, то число степеней свободы вычисляется по формуле 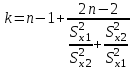 (5) (5)в случае равных объемов выборок или по формуле 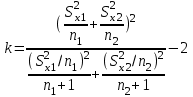 (6) (6)в случае выборок различного объема. Если значение tфакт больше табличного (критического) значения, то различия между выборочными средними считаются достоверными. Пример 1. Пусть среднее значение показателя эритроцитов у одной группы пациентов в количестве 20 человек составляет 4.23, а в другой группе из 28 человек – 4.67. Дисперсии выборок составляют соответственно 1.4 и 1.7. Считая распределение оценок нормальным, а генеральные дисперсии одинаковыми, определить, достоверны ли эти показатели. 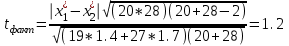 . .Сравниваем полученное значение с табличным значением критерия Стьюдента для k=20+28-2 и уровня значимости 0.05. Оно равно 2.0128 (приложение 2). Таким образом, нулевая гипотеза, утверждающая, что различия между выборочными средними случайны, сохраняется на уровне значимости 5%, т.е. с вероятностью 95% можно утверждать, что различия выборочных средних случайны. Покажем, как выполнить приведенные вычисления в электронной таблице Excel. В ячейки А1-А4 вводим числа 4.23, 4.67, 1.4 и 1.7 соответственно. Формулы в ячейках В1-В6 имеют вид, представленный на рисунке 1. Ячейка В5 содержит значение tфакт, ячейка В6 – табличное значение критерия Стьюдента, вычисляемое с помощью стандартной функции СТЬЮДРАСПОБР (рис.1). 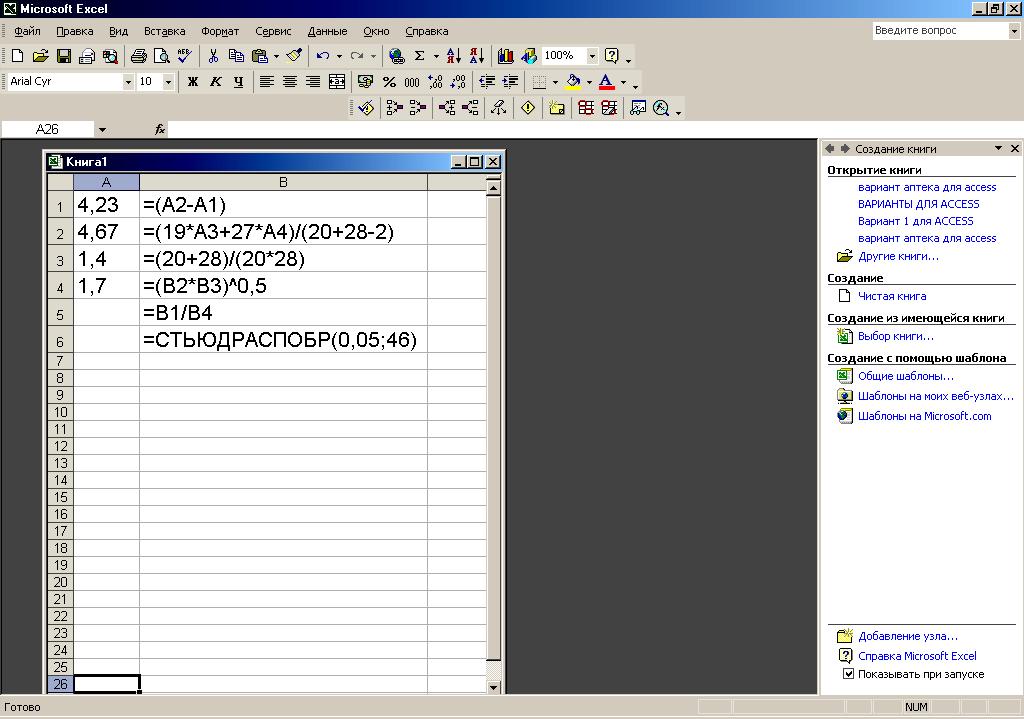 Рис. 1 Строго говоря, применение критерия Стьюдента предполагает равенство генеральных дисперсий сравниваемых совокупностей. Для проверки гипотезы о равенстве генеральных средних вычисляем отношение F= sx12 / sx22 , где числитель представляет собой большую по величине дисперсию, а знаменатель – меньшую. Полученное значение сравнивается с табличным значением критерия Фишера-Снедекора (приложение 7) для заданного уровня значимости и чисел степеней свободы n1 и n2, где n1- уменьшенный на единицу объем выборки для большей дисперсии, n2 - то же самое для меньшей. В Microsoft Excel для проверки гипотезы о равенстве генеральных дисперсий используется функция FРАСП, параметрами которой является вычисленное значение F и степени свободы n1 и n2. Покажем, как выполнить указанную процедуру с помощью пакета анализа Microsoft Excel. В качестве примера рассмотрим данные примера 19. Введем данные первой выборки в ячейки А1-А7, а второй – в ячейки В1-В6. В ячейку А9 вводим формулу =СРЗНАЧ(А1:А7) а в ячейку В9 – формулу =СРЗНАЧ(В1:В6) В ячейку А12 вводим формулу =ДИСПА(А1:А7) а в ячейку В12 – формулу =ДИСПА(В1:В6) Поскольку выборочные дисперсии оказались достаточно различны по значению, то проверяем гипотезу о равенстве генеральных дисперсий. Для этого входим в пункт меню Сервис/Анализ/Двухвыборочный F-тест для дисперсии (рис. 2, 3).  Рис. 2 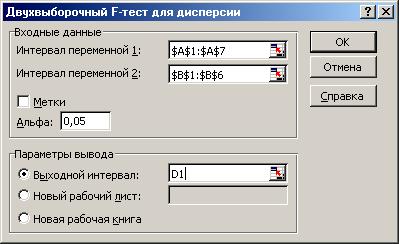 Рис. 3 Так как значение первой выборочной дисперсии (9.14) больше значения второй выборочной дисперсии (4.96), то в качестве интервала переменной 1 указываем диапазон первой выборки, а в качестве интервала переменной 2 – диапазон второй выборки. Если же дисперсия второй выборки больше, то входные данные меняются на противоположные. В качестве выходного интервала указываем любую свободную ячейку рабочего листа, например, D1. В заключение щелкаем мышью на кнопке ОК (рис.3). В результате получим данные представленные на рис. 4. Поскольку значение F=1.84 меньше критического значения 4.95, то на уровне вероятности 95% генеральные дисперсии двух совокупностей равны. В этом случае применяется критерий Сьюдента с одинаковыми дисперсиями. Если же фактической значение F оказывается больше критического, то генеральные дисперсии различны и применяется критерий Сьюдента с различными дисперсиями. 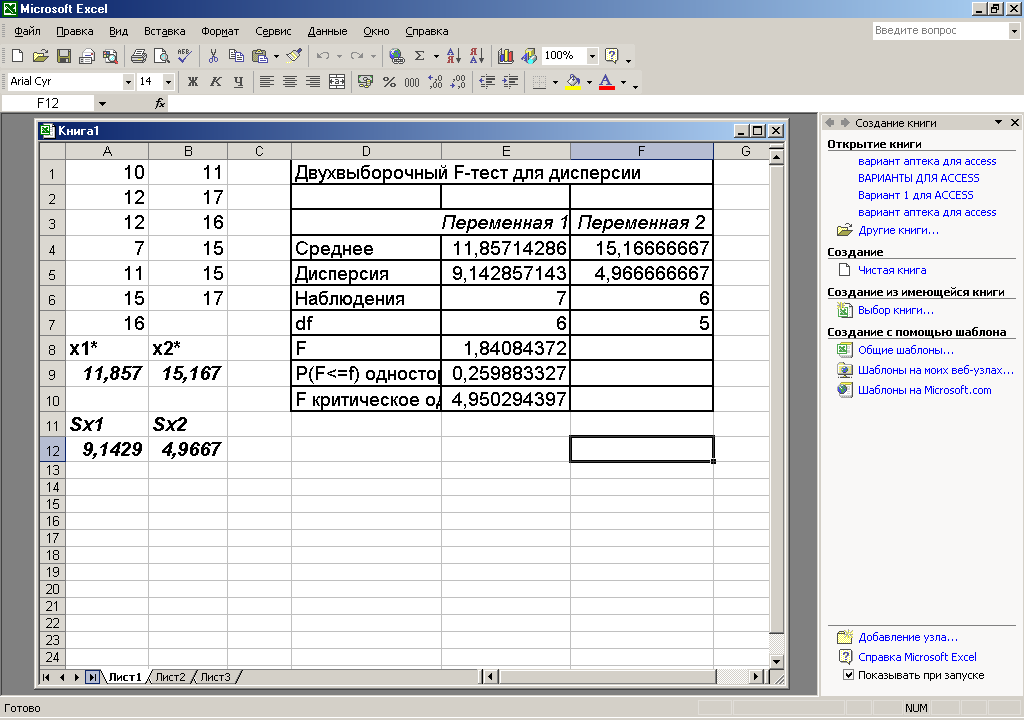 Рис. 4 Снова переходим в пункт меню Сервис/Анализ/Двухвыборочный t-тест с одинаковыми дисперсиями (рис. 5), щелкаем на кнопке ОК и указываем параметры, представленные на рис. 6. В результате получим данные, представленные на рис. 7. Поскольку фактическое значение, называемое t-статистикой(-2.21), по модулю больше критического, равного 2.2009, то нулевая гипотеза отвергается, т.е. различия между выборочнвми средними достоверны.  Рис. 5 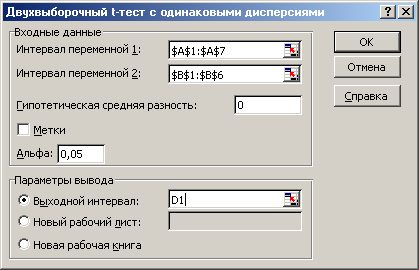 Рис. 6 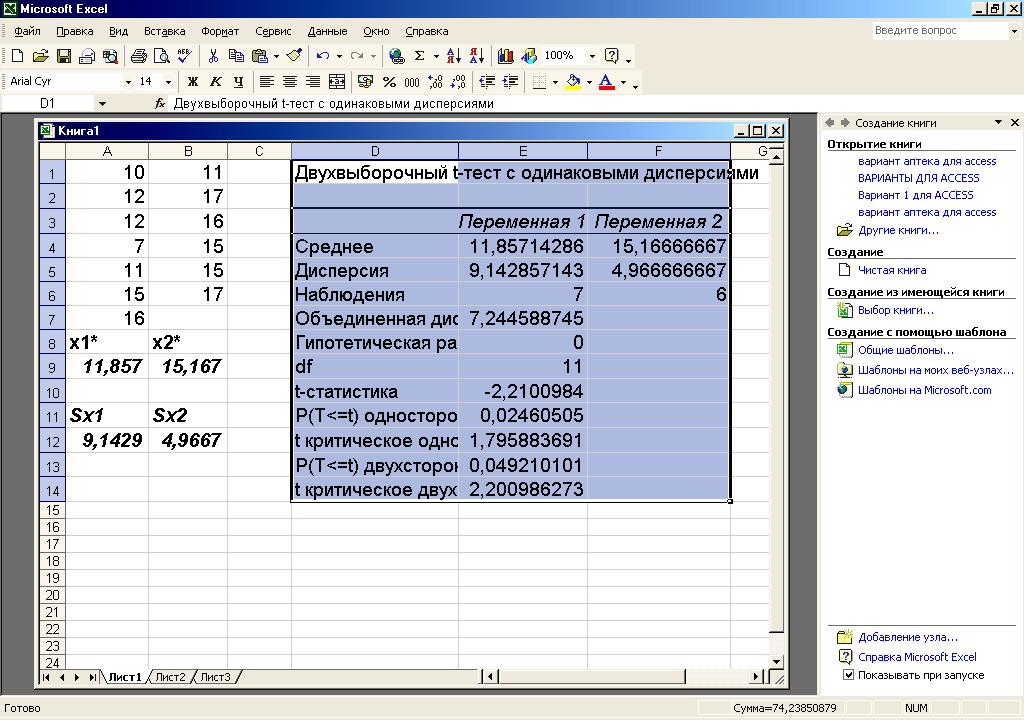 Рис. 7 Другим способом осуществления аналогичной проверки с помощью Microsoft Excel является функция ТТЕСТ. Для обращения к ней, необходимо, находясь в любой свободной ячейке рабочего листа, перейти в меню Вставка/Функция/Статистические и выбрать функцию ТТЕСТ. В поле Массив1 следует указать A1:A7, в поле Массив2 – B1:B6, в поле Хвосты ввести цифру 2, а в поле Тип – цифру 3, после чего щелкнуть кнопку ОК. Получившееся в результате число, определяющее вероятность того, что различия между выборками случайны, сравнивается с заданным уровнем значимости следующим образом: если оно больше заданного уровня значимости, то нулевая гипотеза остается в силе, в противном случае нулевая гипотеза отвергается. В случае малочисленных выборок (n<20) одинакового объема удобнее применять модифицированный критерий Стьюдента. При этом вычисляется значение tфакт по формуле 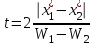 , (7) , (7)где W1 и W2 – размахи выборок, и сравнивается с критическим (приложение 3). Если значение tфакт больше табличного, то нулевая гипотеза отвергается, т.е. различия между выборочными средними достоверны. Если же распределение случайной величины и генеральные дисперсии неизвестны, но выборки достаточно велики (не менее 30 единиц), то в качестве параметрического критерия можно использовать функцию плотности вероятности. Процедура заключается в следующем: сначала вычисляем экспериментальное значение критерия по формуле 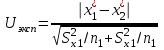 , (8) , (8)где 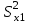 и и 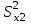 - дисперсии сравниваемых выборок, n1 и n2 – их объемы соответственно, затем полученное значение сравнивается с так называемым критическим значением критерия U, определяемым из соотношения - дисперсии сравниваемых выборок, n1 и n2 – их объемы соответственно, затем полученное значение сравнивается с так называемым критическим значением критерия U, определяемым из соотношения Ф(Uкрит)=(1-p)/2, где Ф(U) – функция плотности вероятности, имеющая вид 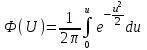 , ,значения которой приведены в приложении 1, р – уровень значимости. При этом если значение Uэксп больше значения Uкрит, то различия между выборками считаются достоверными, в противном случае – случайными. Пример 2. Используя данные примера 1, определим 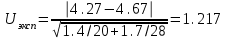 . .Полагая р=0.05, получим Ф(Uкрит)=0.475. По таблице плотности вероятностей (приложении 1) находим значение U, соответствующее числу 0.475. Оно равно 1.96. Таким образом, нулевая гипотеза сохраняется, что согласуется с выводами предыдущего примера. Более простыми в применении являются так называемые непараметрические критерии, используемые в тех случаях, когда распределение случайной величины не соответствует нормальному или просто неизвестно. При применении непараметрических критериев достаточно только вычислить средние двух выборок. Наиболее распространенными непараметрическими критериями являются критерии Ван-дер-Вардена и Уайта, причем критерий Уайта более прост в применении, но может использоваться только для выборок сравнительно небольшого объема (до 35 единиц). Критерий же Ван-дер-Вардена более сложен алгоритмически, требует применения двух таблиц – значений функции ψ(R) и критических значений, но применим к выборкам достаточно большого объема. Рассмотрим применение указанных критериев к одним и тем же данным. Пример 3. Пусть значение СОЭ в одной группе обследуемых, состоящей из 7 человек, составило 10,12,12,7,11,15,16, а в другой группе, состоящей из 6 обследуемых – 11,17,16,15,15,17. Среднее значение для первой выборки составило 11.85 , а для второй – 15.16. Проверим достоверность разницы средних с помощью критерия Ван-дер-Вардена. Составим таблицу (табл.3): Табл.3
|
