Лекция № 8. Лекция Статистические гипотезы
 Скачать 283.14 Kb. Скачать 283.14 Kb.
|
|
Элементы первого и второго столбцов представляют собой варианты первой и второй выборок, при этом варианты, встречающиеся однажды, записываются в соответствующий столбец, а повторяющиеся в выборках – таким образом, чтобы значения в столбцах чередовались. Элементы третьего столбца представляют собой ранги (порядковые номера) вариант в объединенной выборке, состоящей из 13 вариант. Элементы четвертого столбца определяются по таблице (приложение 4). Суммируя элементы четвертого столбца, получим 2.91. Критическое значение же для N=13, разницы в объемах выборок – 1 и уровня значимости 0.05 составляет 2.96 (приложение 5). Таким образом, нулевая гипотеза остается в силе, т.е. различия между выборками случайны. Применим к тем же данный критерий Уайта. Для этого аналогично объединим данные двух выборок в одну, упорядочим объединенную выборку по возрастанию и каждой варианте присвоим ранг, причем одинаковым по значению вариантам присваиваем средний ранг, в результате получим таблицу (табл.4). Табл.4
Суммируя элементы третьего столбца, получим 33.5, четвертого – 57.5. Меньшее из этих чисел (33.5) сравниваем с табличным значением критерия Уайта для N1=7 и N2=6, составляющим 27 (приложение 6). Поскольку вычисленное значение больше табличного, то нулевая гипотеза сохраняется, т.е. различия между выборками случайны. Таким образом, оба критерия в применении к указанному примеру дают одинаковый результат. Для сравнения двух и более независимых выборок целесообразно использовать критерий Неймени, главным условием которого является одинаковый объем всех исследуемых выборок. Пример 4. Пусть изучалась заболеваемость сердечно-сосудистыми заболеваниями (впервые зарегистрировано)в городах А, В и С в период с 1995 по 2004 гг. Данные представлены в таблице 5 в качестве первого, третьего и пятого столбцов. Табл. 5
Объединяем все данные в общую выборку и ранжируем по возрастанию, одинаковым вариантам присваиваем средний ранг (аналогично критерию Уайта), записываем ранги каждой из выборок соответственно во второй, четвертый и шестой столбцы и находим сумму рангов каждой из выборок отдельно. Затем составляем таблицу модулей разностей рангов для каждой пары выборок: Табл.6
Полученные разности сравнивают с табличным значением критерия Неймени (приложение 8). Если величина разности при данном числе наблюдений и количестве выборок превышает табличное, то различия считаются достоверными. В нашем примере при n=10 и k=3 табличное значение составляет 92.3. Поскольку самая большая из разностей не превышает критического значения, то различия в заболеваемости недостоверны. 1б. Если же исследуется действие на выборку некоторого фактора, т.е. необходимо сравнить данные, полученные до и после эксперимента, то применяется парный критерий Стьюдента в случае нормального распределения данных и непараметрический z-критерий знаков при неизвестном распределении. Формула парного критерия Стьюдента имеет вид: 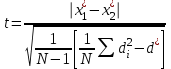 , (9) , (9)где di – разность значений показателя до и после эксперимента для одного и того же i–го объекта, d*- среднее значение разности. Полученное значение t сравнивается с табличным значением критерия Стьюдента для заданного уровня вероятности и числа степеней свободы, равного N-1. Если полученное значение t больше табличного, то нулевая гипотеза отвергается, т.е. различия между выборочными средними достоверны. Пример 5. Пусть в некоторой обследуемых дважды проводился анализ крови на содержание гемоглобина – до и после приема железосодержащего препарата. Результаты приведены в табл. 7. Предполагая, что значение гемоглобина распределяется нормально, проверить гипотезу о том, что повышение уровня гемоглобина вызвано приемом препарата. Будем исходить из нулевой гипотезы, утверждающей, что различия между выборками случайны, т.е. влияние препарата несущественно. Среднее значение гемоглобина до приема составило 9.33 ед., после приема– 12.55. Разница составляет 3.22. Определим значение t по формуле (44) и сравним с табличным значением критерия Стьюдента для принятого уровня значимости и числа степеней свободы, равного N-1. Вычисленное значение t составляет 4.6, табличное – 2.30 для уровня значимости 0.05 и k=9-1=8. Поскольку фактическое значение t больше критического, то нулевая гипотеза отвергается, таким образом, положительное влияние препарата доказано. Табл.7
Покажем, как выполнить приведенные вычисления в электронной таблице EXCEL. В ячейки B1-J1 вводим числа 10,14,17,8,11,12,11,12,13 соответственно, а в ячейки B2-J2 вводим числа 15,14,26,7,15,19,16,18,17 соответственно. В ячейку B3 вводим формулу =B2-B1 и копируем ее в ячейки С3-J3. В ячейку B4 вводим формулу =B3^2 и копируем ее в ячейки С4-J4. В ячейку K1 вводим формулу =СРЗНАЧ(B1:J1) и копируем ее в ячейки K2-K3, а в ячейку K4 вводим формулу =СУММ(B4:J4). В ячейку B6 вводим формулу =ABS(K1-K2)/((K4/9-K3)/8)^(1/2) в результате чего в ячейке B6 появляется значение 4.10. В ячейку B7 вводим формулу =CТЬЮДРАСПОБР(0,05;8) в результате чего ячейка В7 содержит табличное значение критерия Стьюдента для принятого уровня значимости и числа степеней свободы. Ту же процедуру можно проделать с помощью пакета анализа в Microsoft Excel. Для этого переходим в пункт меню Сервис/Анализ/ Парный двухвыборочный t-тест для средних и указываем параметры, представленные на рис. 11. 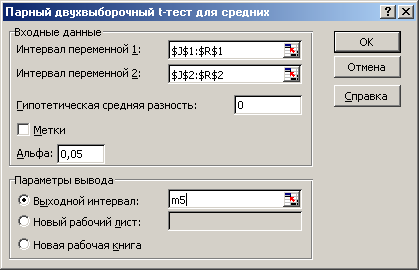 Рис. 11 В результате получим данные, представленные в табл. 8. Поскольку фактическое значение, называемое t-статистикой (-4.11), по модулю больше критического, равного 2.306005626, то нулевая гипотеза отвергается, т.е. различия между выборочными средними достоверны. Табл.8.
Другим способом осуществления аналогичной проверки с помощью Microsoft Excel является та же функция ТТЕСТ. При этом в поле Массив1 следует указать B1:J1, в поле Массив2 – B2:J2, в поле Хвосты ввести цифру 2, а в поле Тип – цифру 1, после чего щелкнуть кнопку ОК. Нулевая гипотеза отвергается, если получившееся значение меньше принятого уровня значимости. Рассмотрим применение z-критерия знаков к попарно связанным выборкам. Суть его заключается в следующем: если действие фактора имеет место, то значения изучаемого признака изменяются в ту или другую сторону, причем чем больше в выборке доля таких изменений (одного знака), тем результативнее действующий фактор. Фактическое значение количества изменений сравнивается с табличным (приложение 9). Нулевая гипотеза отвергается, если фактическое значение больше критического для указанного объема выборок. При этом нулевые разности не учитываются. Применим критерий знаков к примеру 5. Как видно из табл. 7, у большинства обследованных (7 из 9) содержание гемоглобина увеличилось. При обращении к таблице критерия знаков число нулевых разностей не учитывается, таким образом, N=8. Критическое значение для таблицы критерия знаков для уровня значимости 5% и n=8 составляет 7. Таким образом, нулевая гипотеза отвергается. Если объем выборок превышает 90, то в качестве критического значения берется целая часть величины 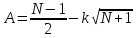 , где k=0.8224 для α=0.01 и k=0.98 для α=0.05. , где k=0.8224 для α=0.01 и k=0.98 для α=0.05.Количество положительных разностей D+ сравнивается с полученным числом; нулевая гипотеза отвергается, если D+ превышает критическое значение. В случае, если направление изменения признака неизвестно (чаще такая ситуация встречается для медико-биологических объектов) то в качестве D берется max{D+,D-} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
