Теория к теме 1. Лекция 1 предмет и метод статистики предмет, метод и основные категории статистики как науки
 Скачать 188.12 Kb. Скачать 188.12 Kb.
|
|
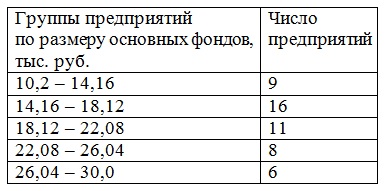
Этапы построения статистических группировок Построение статистических группировок осуществляется по следующим этапам: 1) выбор группировочного признака; 2) определение числа групп; 3) построение интервалов группировки; 4) подсчет групповых итогов и заполнение макета группировки. 1. Выбор группировочного признака Группировочным называется признак, по которому осуществляется разбиение единиц совокупности на отдельные группы. В качестве группировочного могут выступать как количественные, так и качественные признаки. Количественными являются признаки, которые имеют числовое выражение (уставный капитал, прибыль, объем реализованной продукции, балл в сессию, курс акций и т.д.). Качественными называются признаки, которые отражают состояние единицы совокупности (вид экономической деятельности, семейное положение, специальность и т.д.). 2. Определение числа групп Следующим этапом построения статистических группировок является определение числа групп, на которые необходимо разбить изучаемую совокупность единиц наблюдения. Число групп зависит: • от задач статистического исследования; • признака, положенного в основание группировки; • объема изучаемой совокупности; • степени вариации признака. При решении задачи определения чиста групп важно учитывать признак, по которому осуществляется разбиение единиц совокупности на группы, особенно, если в качестве группировочного выступает качественный признак. Так, группировка сотрудников компании по полу может содержать только две группы: "женский" и "мужской", так как признак "пол" по своей сущности имеет только эти две градации. При построении группировки единиц совокупности по количественному признаку особое внимание необходимо обратить на объем изучаемой совокупности и степень вариации признака, положенного в основание группировки. При анализе совокупностей малого объема не следует образовывать большое количество групп, так как группы будут включать в себя недостаточное число единиц совокупности изучаемого объекта. Показатели, рассчитанные для таких групп, не будут представительными и типичными для каждой выделенной группы. Выделение большого числа групп позволит, с одной стороны, точнее воспроизвести характер изучаемого объекта. Однако, с другой стороны, слишком большое число групп затрудняет выявление закономерностей при исследовании социально-экономических явлений и процессов. Степень вариации группировочного признака оказывает существенную роль для определения числа групп. В связи с этим при определении числа групп необходимо принять во внимание размах вариации признака, который определяется по следующей формуле (см. гл. 6): 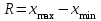 где 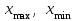 — максимальное и минимальное значение признака в совокупности соответственно. — максимальное и минимальное значение признака в совокупности соответственно.Можно предположить, что чем больше колеблемость, изменяемость значений признака в совокупности, т.е. чем больше размах вариации изучаемого признака, тем большее число групп можно образовать. Однако при этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы совокупности. Определение числа групп можно осуществить несколькими способами. Число групп тесно связано с объемом совокупности, иногда для определения для определения интервала группировок может быть использована формула Стерджесса (обычно при незначительной вариации признаков): 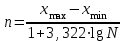 Где 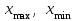 - максимальное и минимальное значение признака ряда распределения; N - число единиц совокупности. - максимальное и минимальное значение признака ряда распределения; N - число единиц совокупности.Например, при 200 единицах совокупности число групп определяется следующим образом: 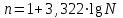 3. Построение интервалов группировки Интервал – очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бывают: 1. открытые, когда имеется только либо верхняя,либо нижняя граница; 2. закрытые, когда имеются и нижняя,и верхняя границы. 3. равные, когда разность между максимальным и минимальным значениями вкаждом из интервалов одинакова; 4. неравные, когда,например,ширина интервала постепенно увеличивается,аверхний интервал часто не закрывается вовсе; Неравные интервалы подразделяют: • на прогрессивно-возрастающие; • прогрессивно-убывающие; • специализированные; • произвольные. При построении прогрессивно-возрастающих и прогрессивно-убывающих интервалов используется принцип арифметической или геометрической прогрессии. Величину интервалов, изменяющихся в арифметической прогрессии, определяют следующим образом: 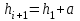 а в геометрической прогрессии 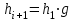 где а — константа (для прогрессивно-возрастающих интервалов имеет знак "+", а для прогрессивно-убывающих -знак "-"); g — константа (для прогрессивно-возрастающих — больше 1; для прогрессивно-убывающих — меньше 1). Специализированными называются интервалы, которые применяются для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях. При изучении социально-экономических явлений на макроэкономическом уровне часто применяют группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни прогрессивно-убывающими. Такие интервалы называются произвольными. Пример: Имеются данные о стоимости основных фондов у 50 предприятий, тыс. руб.
Построить ряд распределения, выделив 5 групп предприятий (с равными интервалами). Решение Для решения выберем наибольшее и наименьшее значения стоимости основных фондов предприятий. Это 30,0 и 10,2 тыс. руб. Найдем размер интервала: h = (30,0-10,2):5= 3,96 тыс. руб. Тогда в первую группу будут входить предприятия, размер основных фондов которых составляет от 10,2 тыс. руб. до 10,2+3,96=14,16 тыс. руб. Таких предприятий будет 9. Во вторую группу войдут предприятия, размер основных фондов которых составит от 14,16 тыс. руб. до 14,16+3,96=18,12 тыс. руб. Таких предприятий будет 16. Аналогично найдем число предприятий, входящих в третью, четвертую и пятую группы.
Полученный ряд распределения поместим в таблицу. 3.3. Статистические таблицы и графики Статистические таблицы являются средством наглядного выражения результатов исследования. Практикой выработаны определенные требования к составлению и оформлению таблиц. Таблица по возможности должна быть краткой. Каждая таблица должна иметь подробное название, из которого становится известно: а) какой круг вопросов излагает и иллюстрирует таблица; б) каковы географические границы представленной статистической совокупности; в) за какой период времени, которому они относятся; г) каковы единицы измерения (если они одинаковы для всех табличных клеток). Если единицы измерения неодинаковы, то в верхних или боковых заголовках обязательно следует указывать, в каких единицах приводятся статистические данные (тонн, штук, рублей и пр.). Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробно раскрывается содержание показателей, даются и другие пояснения, а также оговорки в случае, если таблица содержит данные, полученные в результате вычислений. При оформлении таблиц обычно применяются такие условные обозначения: знак тире (-) - когда явление отсутствует; х - если явление не имеет осмысленного содержания; многоточие (...) - когда отсутствуют сведения о его размере (или делается запись «Нет сведений»). Если сведения имеются, но числовое значение меньше принятой в таблице точности, оно выражается дробным числом (0,0). Округленные числа приводятся в таблице с одинаковой степенью точности (до 0,1; до 0,01 и т. п.). Если в таблице приводятся проценты роста, то во многих случаях целесообразно проценты от 300 и более заменять отношениями в разах. Например, писать не «1000 %», а «в 10,0 раз». Статистическая таблица - это цифровое выражение итоговой характеристики всей наблюдаемой совокупности или ее составных частей по одному или нескольким существенным признакам. Статистическая таблица содержит два элемента: подлежащее и сказуемое. Подлежащее статистической таблицы есть перечень групп или единиц, составляющих исследуемую совокупность единиц наблюдения. Сказуемое статистической таблицы - это цифровые показатели, с помощью которых дается характеристика выделенных в подлежащем групп и единиц. Виды статистических таблиц. 1. Простые таблицах, как правило, содержат справочный материал, в них дается перечень групп или единиц, составляющих объект изучения. При этом части подлежащего не являются группами одинакового качества, отсутствует систематизация изучаемых единиц. Сказуемое этих таблиц содержит абсолютные величины, отражающие объемы изучаемых процессов. Групповые и комбинационные таблицы предназначены для научных целей, где, в отличие от простых таблиц, в сказуемом - средние и относительные величины на основе абсолютных величин. 2. Групповая таблица - это таблица, где статистическая совокупность разбивается на отдельные группы по какому-либо одному существенному признаку, при этом каждая группа характеризуется рядом показателей. Примером такой группировки может быть разделение российских семей на группы по месту проживания (сельское и городское), где образуются подгруппы семей по количеству детей. Анализ этих группировок по материалам переписи 1989 года позволил сделать вывод, что большинство семей, независимо от принадлежности к городскому или сельскому населению, имеют только по одному ребенку. 3. Комбинационная таблица - это таблица, где подлежащее представляет собой группировку единиц совокупности по двум и более признакам, которые распределяются на группы сначала по одному признаку, а затем на подгруппы по другому признаку внутри каждой из уже выделенных групп. Комбинационная таблица устанавливает существенную связь между факторами группировки. Примером комбинационной группировки может быть распределение полиграфических предприятий по трем существенным признакам: степени оснащенности современным полиграфическим оборудованием, степени применения современных технологий и уровню производительности труда. Такого рода статистические таблицы позволяют осуществить всесторонний анализ, но они менее наглядны. Использование графиков для изложения статистических показателей позволяет придать последним наглядность и выразительность, облегчить их восприятие, а во многих случаях помогает уяснить сущность изучаемого явления, его закономерности и особенности, увидеть тенденции его развития, взаимосвязь характеризующих его показателей. Статистические графики можно классифицировать по разным признакам: назначению (содержанию), способу построения и характеру графического образа. По содержанию или назначению можно выделить графики сравнения в пространстве, графики различных относительных величин (структуры, динамики и т. п.), графики вариационных рядов, графики размещения по территории, графики взаимосвязанных показателей. Возможны и комбинации этих графиков, например графическое изображение вариации в динамике или динамики взаимосвязанных показателей и т. п. По способу построения графики можно разделить на диаграммы, картодиаграммы и картограммы. По характеру графического образа различают графики точечные, линейные, плоскостные (столбиковые, почасовые, квадратные, круговые, секторные, фигурные) и объемные. Полигон распределения представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующегося признака, а ординатами - соответствующие им частоты. 23456 число живущих в квартире. |