Лекция 10. Кручение

• Название: Лекция 10. Кручение
• Дата: 26.01.2021
• Размер: 1.98 Mb.
• Имя файла: Loeng_10_Kruchenije_izgib.doc
• Тип: Лекция; #171383

Лекция 10.

КРУЧЕНИЕ

Чистый сдвиг
Экспериментально чистый сдвиг может быть осуществлен при кручении тонкостенной трубы (рис. 79, а), поэтому деформация чистого сдвига отнесена к теме «кручение».

Рассмотрим элемент abed, вырезанный из тонкостенной трубы (рис. 79, б).

При возникновении касательных напряжений элемент перекашивается. Если считать грань ad закрепленной, то грань bс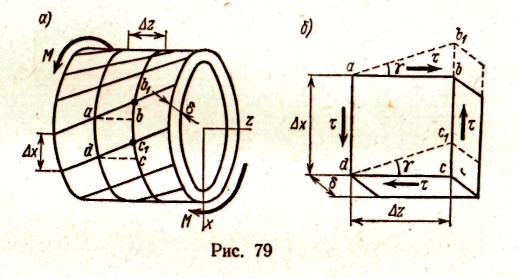



сдвинется в положение b₁c₁. Прямые углы между гранями изменяются на величину γ. Угол γ , представляющий собой изменение первоначально прямого угла между гранями элементарного параллелепипеда, называется углом сдвига.
Касательные напряжения τ и угол сдвига γ, называемый также относительным сдвигом, связаны прямой пропорциональностью, то есть законом Гука:



Входящая в эту формулу величина G называется модулем сдвига. Эта величина характеризует жесткость материала при деформации сдвига. Так как γ выражается отвлеченным числом, то модуль сдвига G, как и модуль продольной упругости Е, имеет ту же единицу измерения, что и напряжение: МПа, Н/мм², кгс/см².
Между модулем упругости Е и модулем сдвига G существует зависимость, которую приводим без вывода:



где μ — коэффициент поперечной деформации (коэффициент Пуассона).
Для стали μ = 0,25; G = 0,4 Е = 0,4^.2^.10⁵ = 8^.10⁴ МПа. Приведенные соотношения между G и Е подтверждаются опытами.
Основные понятия. Эпюры крутящих моментов
На кручение обычно работают брусья круглого поперечного сечения, например валы и витки цилиндрических пружин.
Кручение возникает при нагружении бруса парами сил, расположенными в плоскостях, перпендикулярных продольной оси бруса (рис. 80).

Моменты этих пар M_вр называют вращающими моментами. Их алгебраическая сумма равна нулю, если вал находится в равновесии и вращается равномерно. Величину вращающего момента М_вр можно вычислить по передаваемой мощности Р и частоте вращения n:


Эта формула дает величину момента в Н^.м, если мощность выражена в Вт, а частота в об/мин.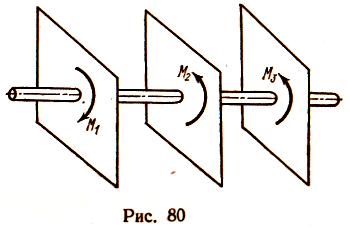


Момент внутренних сил относительно продольной оси бруса называют крутящим моментом М_к. При кручении в поперечных сечениях бруса возникает один внутренний силовой фактор — крутящий момент М_к. Он определяется при помощи метода сечений.
Когда вращение от двигателя передается при помощи передаточного вала нескольким рабочим машинам, крутящий момент не остается постоянным по длине вала. Характер изменения кру­тящего момента по длине вала наиболее наглядно может быть представлен эпюрой крутящих моментов. Рассмотрим построение такой эпюры для вала, на котором закреплено несколько шкивов (рис. 81, а); шкив / получает вращение от двигателя, шкивы //, III и IV передают его станкам. Моменты, передаваемые каждым шкивом на вал, вычисляют по формуле (65). Направление момента М₁ противоположно направлению моментов М₂, М₃ и M₄. При установившемся движении (равномерном вращении вала), пренебрегая трением в подшипниках, получаем из условия равновесия вала:



Крутящий момент изменяется в сечениях вала, передающих внешние моменты от шкивов. Разделим вал на три участка (рис. 81, а) и определим крутящие моменты в поперечных сечениях каждого из них. Крутящий момент в любом поперечном сечении первого участка между шкивами II и I уравновешивает момент внешней пары М₂, действующей на левую отсеченную часть, т.е. Мк₁ = М₂.

Дальше текст отсутствует – не знаю, по какой причине. Извините! (стр.84)

(стр.88, страницы 84-87 почему-то не были отсканированы)
ной на расстоянии р от оси бруса, xdA, а ее момент относительно оси бруса равен xdAp.

Сумма моментов всех элементарных внутренних касательных сил, возникающих в поперечном сечении, представляет собой крутящий момент Мк в данном сечении и определяется интегралом, взятым по всей площади

Выражая т через тгаах т = ттахр/г и вынося затем постоянный множитель тшах/г за знак интеграла, получаем



Интеграл , как известно из предыдущего (см. § 25),

представляет собой полярный момент инерции сечения



Таким образом, , откуда

н соответственно



Выведенная формула определяет касательное напряжение в лю­бой точке поперечного сечения при кручении вала круглого по­перечного сечения. Напряжения в точках, близких к оси вала, малы, поэтому для уменьшения его массы иногда удаляют вну­треннюю часть и делают его полым — с кольцевым сечением. Наибольшего значения достигают напряжения в поперечном сече­нии в точках у поверхности, т. е. в точках, наиболее удаленных от его оси. . Формулу (69) для тшах можно представить в виде



Отношение Jp/r = Wp называют полярным моментом сопро­тивления сечения.

Полярный момент сопротивления круга вычислим, разделив величину Jp на радиус г = 0,5d,



Аналогично для кольцевого сечения

где а — djdn.

Определим угол закручивания бруса, изображенного на рис. 85, а. Исходя из уравнений ушах = (рг/1 и тшах = GYmax, находим

Подставляя тшах = -, окончательно получаем



Величина угла ср выражается в радианах. Угол поворота по формуле (74) можно определять лишь для участка бруса, имеющего постоянное поперечное сечение, при условии, что крутящий мо­мент по длине этого участка не изменяется.
Расчеты на прочность и жесткость при кручении
Прочность при кручении бруса круглого сплошного или кольцевого поперечного сечения определяется условием



Формула (75) может служить основой для трех видов расчетов.
1. Проверка прочности (проверочный расчет), когда известны наибольший крутящий момент и размеры поперечного сечения вала. Расчет производится непосредственно по формуле (75).
2. Подбор сечения (проектный расчет). Решив неравенство (75) относительно Wp, получим формулу для определения полярного момента сопротивления, а значит диаметра вала, исходя из условия прочности



Требуемый диаметр вала при найденном значении Wp. определяется из формулы (72) или (73).
3. Определение допускаемого крутящего момента, когда известны размеры сечения вала и задано допускаемое напряжение,



Допускаемое напряжение для валов из сталей марок сталь 40 и сталь 45 принимается в пределах [τ_к] = 30-50 МПа. Кроме соблюдения условия прочности при проектировании валов требуется, чтобы вал обладал достаточной жесткостью, т. е. чтобы угол закручивания не превосходил некоторой заданной величины. Так, в зубчатых передачах при значительных углах закручивания валов зубья колес перекашиваются. Следствием может быть выкрашивание поверхностей зубьев и поломка передачи, поэтому необходимая жесткость валов практически всегда должна быть обеспечена. Обозначив через 0 угол закручивания единичной длины вала, можно составить расчетную формулу для проверки вала на жесткость:



В зависимости от назначения вала принимают [θ] = (0,45-l,75)^. 10^-2 рад/м, что соответствует [θ°] = (0,25-1,0) град/м.

Если вычислить относительный угол закручивания в градусах на 1 м длины вала, вместо формулы (78) получим



С помощью формул (78) и (79) решаются три задачи, аналогичные задачам расчета на прочность.

1. Проверка жесткости (проверочный расчет), когда заданы крутящий момент, размеры и материал вала, а также допускаемый уюл закручивания.

2 Подбор сечения по условию жесткости (проектный расчет) Из неравенства (78) получим формулу для определения полярного момента инерции сечения вала, по условию жесткости



При найденном значении Jp диаметр вала определяют из формул (38) и (39).

3. Определение допускаемого крутящего момента по условию жесткости


Пример. По данным примера 16 определить диаметр вала, удовлетворяющий условиям прочности и жесткости на наиболее напряженном участке. Материал вала — сталь 40. Допускаемое напряжение на кручение [τ_к] = 30 МПа, допускаемый угол закручивания [θ°] = 1^.10^-2 рад/м = 10^.10^-5 рад/мм; модуль сдвига G = 8^.10⁴ Н/мм².
Решение. По эпюре крутящих моментов (см. рис. 82) видно, что наибольший крутящий момент Мк = 2067 Нм.

По условию прочности на кручение [см. формулу (76)] определяем:



Выражая полярный момент сопротивления через диаметр вала Wp ≈ 0,2d³, находим его значение



По условию жесткости [см. формулу (80)] определяем полярный момент инерции



С другой стороны, выражая полярный момент инерции через диаметр вала Jp = 0,1 d ⁴, находим его значение



Окончательно принимаем диаметр вала по условию жесткости


Пример. В поперечных сечениях стального вала возникает крутящий момент Мк = 2000 Нм. Диаметр вала d = 65 мм, модуль сдвига G = 0,8^.10⁵ Н/мм². Проверить прочность и жесткость вала, если допускаемое напряжение [тк] = 40 МПа, а допускаемый угол закручивания [6°] = 0,85 град/м.
Решение. Прочность вала проверяем по формуле (75)

где



Для проверки жесткости вычислим значение полярного момента инерции



Величину допускаемого угла закручивания переводим в радианы на 1 мм!



Подставив в формулу (78) значения Jp и [б], получим



Следовательно, в этом примере диаметр вала удовлетворяет и условию прочности, и условию жесткости.
Упражнение

1. Справедлив ли закон Гука при кручении, если напряжение не превышает предела пропорциональности?

А. Справедлив. Б. Не справедлив.

2. Вычислите полярный момент сопротивления сечения круглого сплошного вала d = 30 мм.

3. Укажите, для какой точки поперечного сечения (рис. 86) можно вычислить напряжения по формуле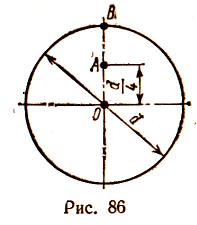



А. Для точки А. Б. Для точки В. В. Для точки О.

4. Во сколько раз напряжение в точке А (рис. 86) меньше напряжения в точке б?

А. В четыре раза. Б. В два раза.

Изобразите эпюру касательных напряжений в поперечном сечении вала.
5. Зависит ли величина рабочих (расчетных) касательных напряжений от

материала вала?

А. Зависит. Б. Не зависит.
6. Зависит ли угол поворота сечения вала от материала, из которого он

изготовлен?

А. Зависит. Б. Не зависит.
7. Во сколько раз уменьшится максимальное напряжение в поперечных

сечениях вала, если его диаметр увеличить в два раза?

А. В два раза. Б. В четыре раза. В. В восемь раз.
ИЗГИБ

Основные понятия
Элементы конструкций, работающих на изгиб, называют бал­ками. Чаще всего встречается поперечный изгиб, когда внешние силы, перпендикулярные к продольной оси балки, действуют в плоскости, проходящей через ось балки и одну из главных цен­тральных осей ее поперечного сечения, в частности, в плоскости, совпадающей с плоскостью симметрии балки, например, сила F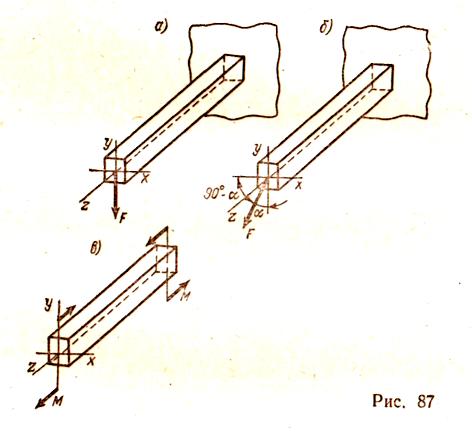



на рис. 87, а. Такой изгиб называют прямым. Если же силы, вы­зывающие деформацию изгиба, действуют в плоскости, проходя­щей через ось балки, но не проходящей через одну из главных центральных осей ее поперечного сечения, имеет место косой изгиб (рис. 87, б).

В поперечных сечениях балок при изгибе возникают два вну­тренних силовых фактора: изгибающий момент и поперечная сила. Однако возможен такой частный случай, когда в поперечных сечениях балки возникает только один силовой фактор — изгиба­ющий момент, а поперечная сила равна нулю. В этом случае изгиб называют чистым. Он возникает, в частности, когда балка изгибается двумя противоположно направленными парами сил, приложенными к ее торцам (рис. 87, в). Чистый изгиб возникает при некоторых нагружениях сосредоточенными силами или рас­пределенной нагрузкой.

Упражнение 23

1. В поперечном сечении балки возникли изгибающий момент и поперечная
сила. Укажите вид изгиба.

А. Чистый изгиб. Б. Поперечный изгиб.

2. Какой вид уравнений равновесия наиболее целесообразно использовать
для определения реакций опор балки, изображенной на рис. 88.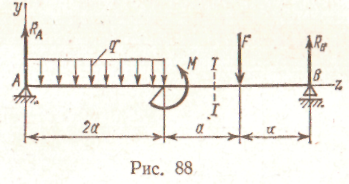





3. Найдите ошибки в приведенных ниже уравнениях равновесия для балки,-
изображенной на рис. 88: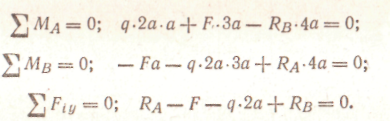



§ 47. Нормальные напряжения при изгибе

Нанесем на боковую поверхность балки, испытывающей чи­стый изгиб (рис. 101, а), продольную линию 00х на половине высоты и ряд поперечных параллельных между собой линий. При нагружении двумя противоположно направленными парами сил, действующими в продольной плоскости симметрии (рис. 101, б), балка деформируется — изогнется выпуклостью вниз. Линии на боковой поверхности балки останутся прямыми,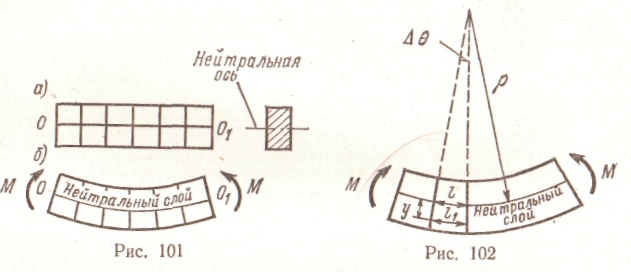



но параллельность их нарушится. Расстояния между концами этих линий на выпуклой стороне увеличатся, а на вогнутой умень­шатся. Расстояния между этими линиями на половине высоты балки останутся такими же, как до деформации. Из этого можно заключить, что при изгибе продольные волокна балки на выпук­лой стороне удлиняются, а на вогнутой укорачиваются; слой волокон, лежащих на половине высоты балки, сохраняет, искри­вившись, неизменную длину.

Растягивающие и сжимающие напряжения в поперечных сече­ниях балки соответствуют удлинению и укорочению ее продольных волокон. Слой, длина которого не изменяется при изгибе, не испытывает напряжений и называется нейтральным слоем.

Итак, при изгибе поперечные сечения, оставаясь плоскими, поворачиваются одно относительно другого вокруг некоторых осей, лежащих в их плоскостях. Каждое поперечное сечение поворачивается вокруг линии его пересечения с нейтральным слоем. Эта линия называется нейтральной осью поперечного се­чения.

Высказанное положение носит название гипотезы плоских сечений.

Деформации волокон не зависят от положения волокон по ширине балки. Следовательно, нормальные напряжения, изме­няясь по высоте сечения, остаются одинаковыми по ширине балки.

Исходя из этих гипотез, найдем величину удлинения какого-либо волокна балки при чистом изгибе. Положим, что два близких поперечных сечения балки (рис. 102) повернулись одно относи-

Отношение осевого момента инерции к расстоянию до наиболее удаленных от нейтральной оси волокон симметричного сечения называют осевым моментом сопротивления



Наибольшее по абсолютному значению нормальное напряжение в симметричном сечении (растягивающее или сжимающее) может быть определено по формуле

(89)

Формула (87) для определения нормальных напряжений вы­ведена для чистого изгиба. Однако ею можно пользоваться и

в общем случае прямого поперечного изгиба, когда в сечениях возникает не только изгибающий момент, но и поперечная сила. Поперечные силы, как показывают опыт и теоретические исследо­вания, практически не влияют на нормальные напряжения. Опасным в отношении нормальных напряжений в балках с постоянным сечением будет сечение, в кото­ром изгибающий момент имеет наибольшее абсолютное значение.

Упражнение 27

В каких единицах измеряется осевой момент инер­ции сечения? А. м4. Б. м3. В. ма.


Зависят ли значения нормальных напряжений от формы поперечных сечений балки?

А. Зависят. Б. Не зависят.

3. В каких точках поперечного сечения балки возни­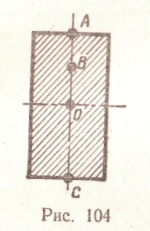
кают наибольшие нормальные напряжения (рис. 104)?

А. В точке О. Б. В точке Л. В. В точке В.


Чему равен осевой момент сопротивления прямоугольника и круга?

Укажите, для какой точки поперечного сечения балки (рис. 104) нормаль­ные напряжения могут быть вычислены по формуле



А. Для точки О. Б. Для точки В. В. Для точек Л и С.

§ 48. Расчеты на прочность при изгибе

Проверку прочности и подбор сечений изгибаемых балок обычно производят исходя из следующего условия: наибольшие нормальные напряжения в поперечных сечениях не должны превосходить допускаемых напряжений [а] на растяжение и сжа­тие, установленных нормами или опытом проектирования для материала балки.

Для балок из материалов, одинаково сопротивляющихся растяжению и сжатию (сталь, дерево), следует выбирать сечения, симметричные относительно нейтральной оси (прямоугольное, круглое, двутавровое), чтобы наибольшие растягивающие и сжи­мающие напряжения были равны между собой. В этом случае условие прочности по нормальным напряжениям имеет вид



Ниже приведены формулы для вычисления моментов сопроти­вления некоторых сечений.

Для прямоугольника (см. рис. 50, а)



Для круга (см. рис. 50, б):



приближенно для круга можно считать Wx та 0, Id3.

Для кольца (см. рис. 49, б)



где а = djdn — отношение внутреннего диаметра кольца к на­ружному.

Для балок, изготовленных из материалов, неодинаково сопро­тивляющихся растяжению и сжатию (например, из чугуна), выгодны сечения, несимметричные относительно нейтральной оси. В этом случае прочность по нормальным напряжениям проверяют по формулам: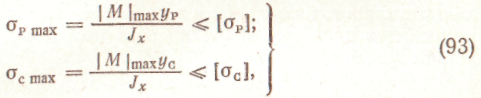

где yр и yG— расстояния от нейтральной оси х до наиболее уда­ленных точек в растянутой и сжатой зонах сечения; [стр] и [сг0] — допускаемые напряжения на растяжение и сжатие.

Использование материала будет наилучшим, когда ор шах = = [сгр], а сСШах = [ас]; для этого необходимо условие



т. е. расстояния нейтральной оси от наиболее удаленных точек в растянутой и сжатой зонах сечения должны быть пропорци­ональны соответствующим допускаемым напряжениям.

Формула напряжений при изгибе выведена на основании закона Гука и потому справедлива только при напряжениях, не превышающих предела пропорциональности материала балки.

С помощью условия прочности по нормальным напряжениям при изгибе можно решать следующие три задачи.

Проверка прочности (проверочный расчет) производится в том случае, когда известны размеры сечения балки, наибольший изгибающий момент и допускаемое напряжение [а]. При этом непосредственно используется условие (90).

Подбор сечения (проектный расчет) производится в том случае, когда заданы действующие на балку нагрузки, т. е. можно определить наибольший изгибающий момент | M|шах и допуска­емое напряжение [а].

Решая неравенство (90) относительно Wx, получаем



По необходимому моменту сопротивления Wx, задавшись формой сечения, подбирают его размеры.

3. Определение наибольшего допускаемого изгибающего мо­
мента производится в том случае, когда заданы размеры сечения
балки и допускаемое напряжение



Наиболее выгодны такие формы сечений, которые дают наи­больший момент сопротивления при наименьшей площади. Такому условию в первую очередь удовлетворяет двутавровое сечение, у которого почти весь материал отнесен от нейтральной оси к верх­ней и нижней полкам, что увеличивает момент инерции Jx, а соот­ветственно и момент сопротивления Wх. Менее выгодно прямо­угольное сечение; круглое сечение еще менее выгодно, так как оно расширяется к нейтральной оси. Полые сечения всегда выгод­нее равновеликих им сплошных сечений.

Целесообразно применять сечения балок из прокатных профи­лей: двутавров, швеллеров и т. п. В сортаменте для этих профилей приводятся числовые значения всех необходимых геометрических ■ характеристик.

Различные варианты расчета балок на прочность показаны на примерах.

Пример 20. Наибольший изгибающий момент в поперечном сечении балки Мтах == 37,5 кН- м. Подобрать сечение стальной балки в трех вариантах: а) про­катный двутавр; б) прямоугольник с отношением высоты к ширине h : Ъ = = 4:3; в) круг.

Определить отношение массы балок прямоугольного и круглого сечения к массе балки двутаврового сечения. Допускаемое напряжение [о] = 160 Н/мм2 (МПА).

Решение. Требуемый момент сопротивления



Подбираем сечение балки в трех вариантах.

Сечение—прокатный двутавр. По таблице ГОСТ 8239—72 подходит двутавровый профиль № 20а. Его момент сопротивления Wx = 237 см3, пло­щадь сечения А = 35,5 см2.

Сечение — прямоугольник с отношением сторон h : Ь = 4 : 3, для пря­моугольника Wx = b№/6; подставив сюда b = 0.75h и приняв равным требуемому значению, получим



откуда



Площадь сечения A2 = 12,3-9,2 = 113 см2.

3. Сечение — круг

откуда

Площадь поперечного сечения круга



Отношение масс, равное отношению площадей сечений:



Следовательно, балка прямоугольного сечения тяжелее двутавровой балки в 3,18 раза, а балка круглого сечения тяжелее двутавровой в 3,97 раза.

Упражнение 28

1. В каком из двух вариантов нагружёния (рис. 105) двутавровая балка
сможет выдержать большую силу F? Длина консолей / в обоих случаях одинакова.

А. По рис. 105, а. Б. По рис. 105, б. В. В обоих случаях балка может вы­держать одинаковую нагрузку.

2. Во сколько раз уменьшатся нормальные напряжения в прямоугольном

сечении балки, если ее высота увеличится в два раза?

А. В два раза. Б. В четыре раза. В. В восемь раз.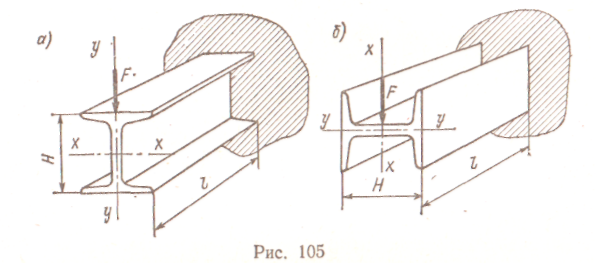



3. По заданному изгибающему моменту при одинаковых допускаемых на­
пряжениях были подобраны прямоугольные сечения балок в трех вариантах
с разными соотношениями высоты h и ширины Ь: вариант I h : b = 2; вариант II
h: b = 3; вариант III h : b = 2,5. Какая из балок будет иметь наименьшую
массу?

§ 51. понятие о теориях прочности

Испытания материалов позволяют определить опасные, или предельные, напряжения при каких-то простейших деформирован­ных состояниях.

Механические испытания материалов можно осуществлять и при сложных видах деформированного состояния, но в этом случае разрушение наступает при различных величинах силовых факторов в сечении и зависит от их соотношения. Действительно, при совместном действии изгиба и кручения вал может раз­рушиться при большом изгибающем и малом крутящем моментах или, наоборот, разрушение может произойти при малом изгиба­ющем, но большом крутящем моментах. Каждому отношению величин изгибающего и крутящего моментов соответствует опре­деленная величина напряжений, вызывающих разрушение вала. Определить опытным путем предельные или опасные напряжения для сложного напряженного состояния при всех возможных ком­бинациях силовых факторов невозможно из-за трудности поста­новки опытов и практически неограниченного объема испытаний.

Появляется необходимость найти способ составления условий прочности при сложном напряженном состоянии, пользуясь вели­чинами предельных напряжений, полученными из опытов для

простого напряженного состояния, например для растяжения. Эта задача может быть решена лишь на основании некоторых предположений (гипотез) о том, какой фактор вызывает появление опасного состояния.

Даже при осевом нагружении стержня таких факторов можно указать несколько. Можно полагать, что опасное состояние воз­никает при достижении нормальными напряжениями предела текучести или предела прочности. Можно также полагать, что опасное состояние возникает, когда наибольшее относительное удлинение достигает определенного значения. Возможно и третье предположение: появление опасного состояния связано с тем, что касательные напряжения достигают определенного значения. Возникновение опасного состояния можно связать также с дости­жением определенного значения энергии, накапливаемой в мате­риале при деформации.

Для осевого растяжения или сжатия все высказанные гипо­тезы дают одинаковые результаты. Иначе обстоит дело в случае сложного напряженного состояния.

В зависимости от принятой гипотезы прочности определяют эквивалентное напряжение сгэ1Ш, которое можно сопоставить с напряжением при осевом нагружении. В соответствии с условием прочности эквивалентное напряжение не должно превышать до­пускаемое напряжение для материала