Лекция 2(1). Определители
 Скачать 302.5 Kb. Скачать 302.5 Kb.
|
|
Лекция 2(1). Определители Перестановка, транспозиция, инверсия. Четность (нечетность) перестановки. Определитель Вычисление определителей с помощью свойств определителей. Возьмем первые Пример 1. Наборы Число различных перестановок из Если в некоторой перестановке поменять местами два числа (не обязательно соседние), то получится новая перестановка. Такое преобразование перестановки называется транспозицией. Пример 2. Перестановка В перестановке Пример 3. Перестановка Перестановка называется четной (нечетной), если она содержит четное(нечетное) число инверсий. Перестановка Отметим без доказательства следующее важное свойство перестановки: любая транспозиция перестановки меняет ее четность. Пример 4. Рассмотрим четную перестановку Четность (нечетность) перестановки Перестановка будет четной (нечетной), если для этого требуется провести четное (нечетное) число транспозиций. Пример 5. Перестановку С каждой квадратной матрицей Если 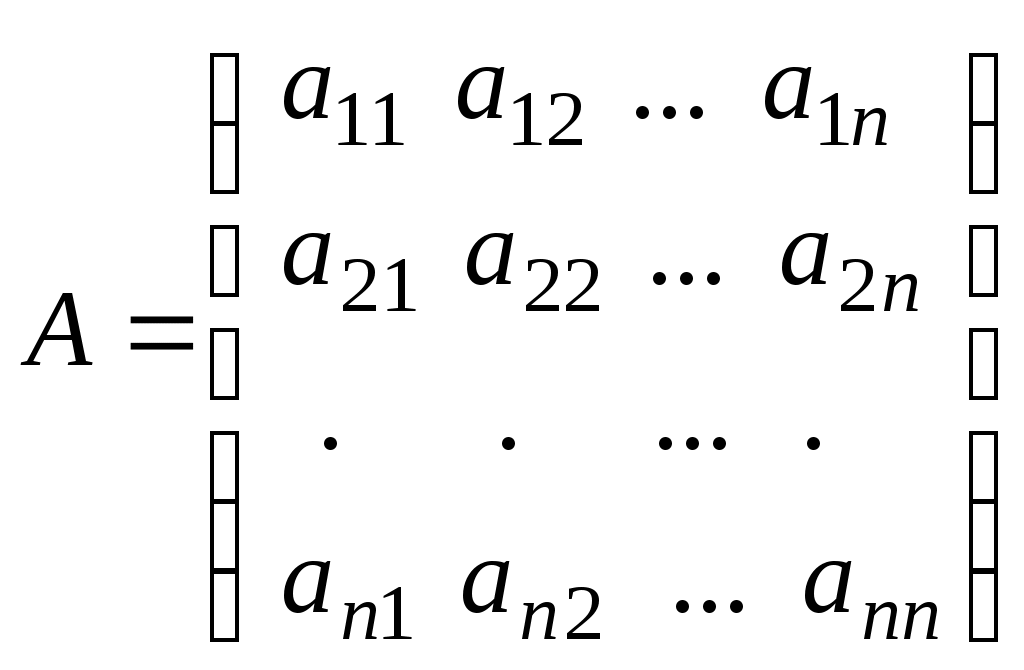 - квадратная матрица - квадратная матрица 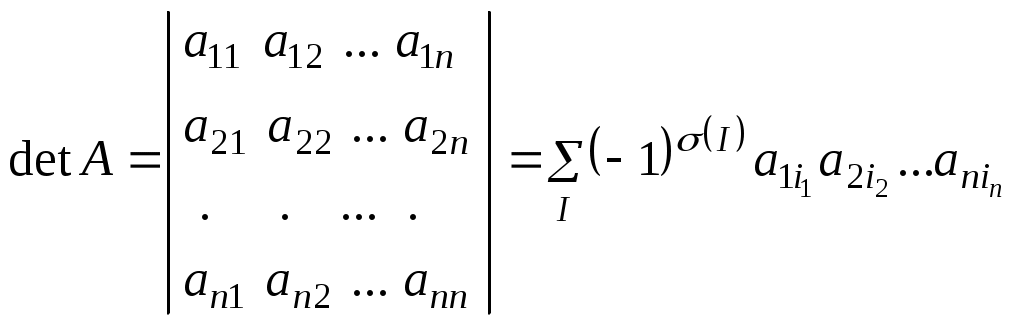 , (1) , (1)где сумма берется по всем Выясним, к каким результатам приводит формула (1) для определителей 1,2,3-го порядка. 1) Пусть 2) Пусть 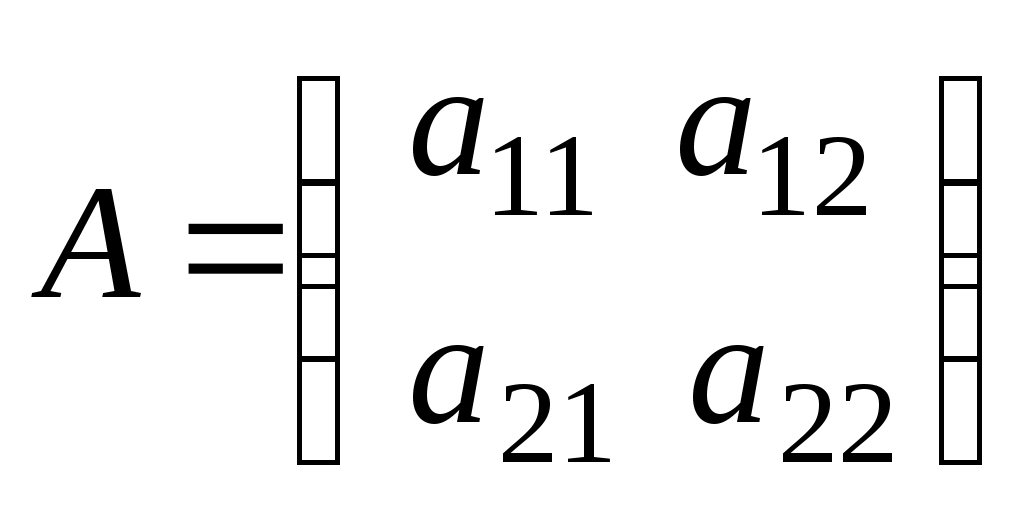 - квадратная матрица 2-го порядка. Количество всех перестановок - квадратная матрица 2-го порядка. Количество всех перестановок Следовательно, согласно формуле (2.1) определитель 2-го порядка равен 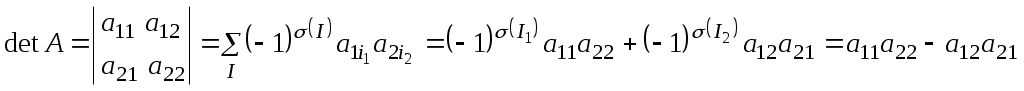 . .В результате получаем, 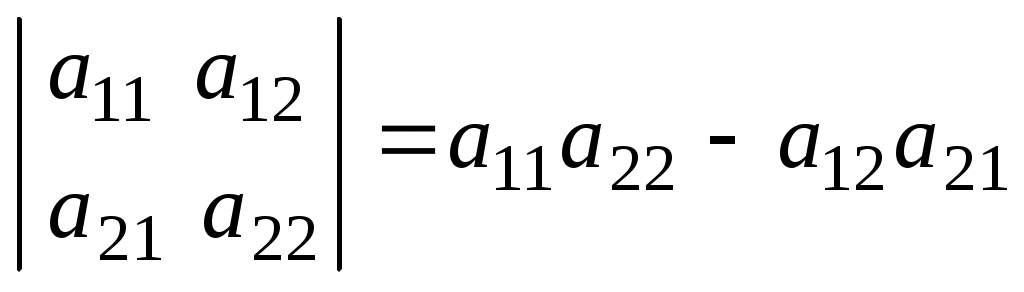 . (2) . (2)3) Пусть 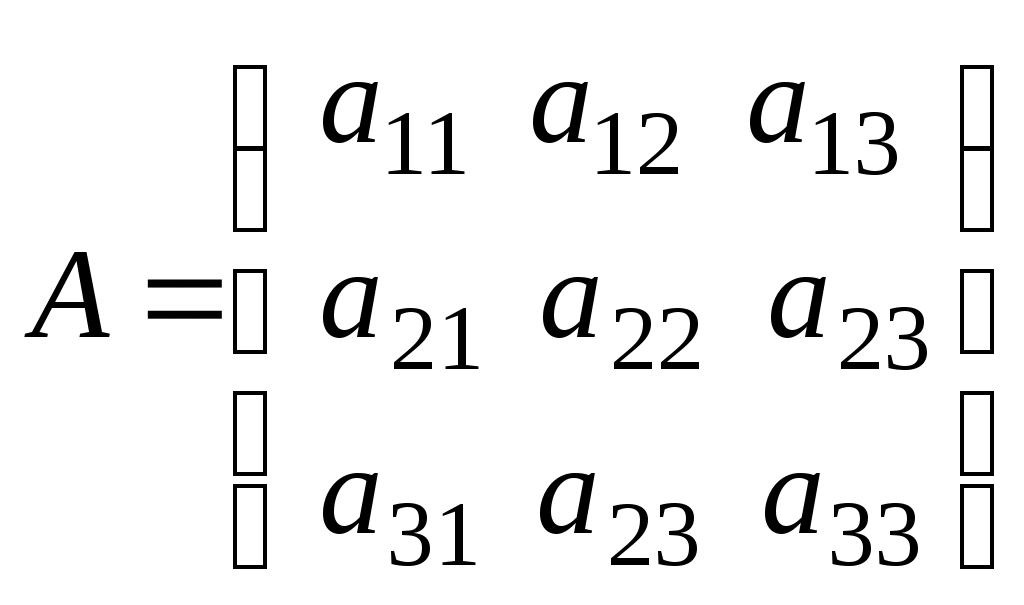 - квадратная матрица 3-го порядка. Количество всех перестановок - квадратная матрица 3-го порядка. Количество всех перестановок Таким образом, в силу (1) определитель 3-го порядка равен 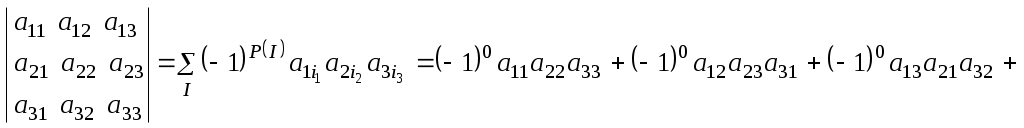 Окончательная формула для вычисления определителя 3-го порядка имеет такой вид 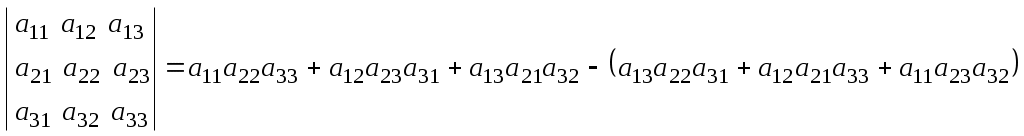 (3) (3)Формулы (2), (3) вычисления определителей 2-го и 3-го порядков называются правилами Саррюса. Их легко запомнить и использовать при вычислении определителей 2-го и 3-го порядков. Пример 6. 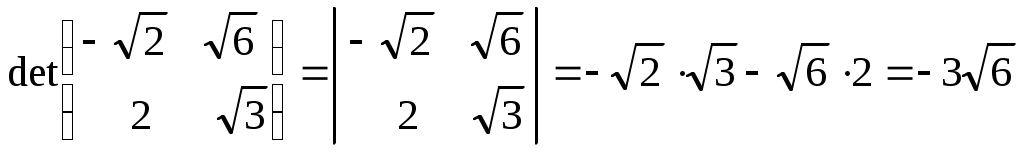 . .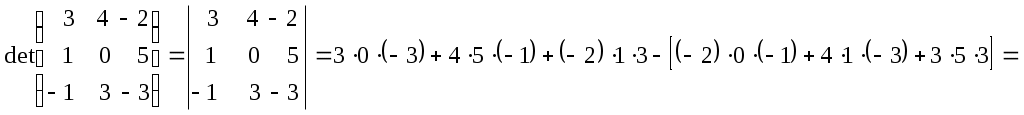 Вычисление определителей 4-го, 5-го и более высокого порядка по определению становится громоздким и неэффективным из-за большого количества слагаемых в правой части формулы (1). Так, определитель 4-го порядка имеет 4!=24 слагаемых, определитель 5-го порядка имеет 5!=120 слагаемых и т.д. Поэтому, на практике вычисление определителей высокого порядка проводится другими методами. Один из этих методов основан на свойствах определителей, которые позволяют проводить простые операции с его строками и столбцами. Они упрощают заданный определитель до такого состояния, когда его вычисление становится элементарным. Сформулируем без доказательства эти свойства, которые верны для определителей любого порядка. Покажем действие свойства 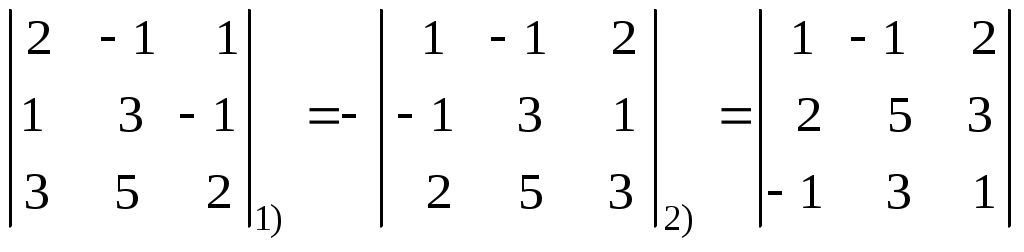 . .Здесь над определителем проведены следующие преобразования: 1) в заданном определителе поменяли местами 1-й и 3-й столбцы; 2) во втором определителе поменяли местами 2-ю и 3-ю строчки. Приведем действие свойства 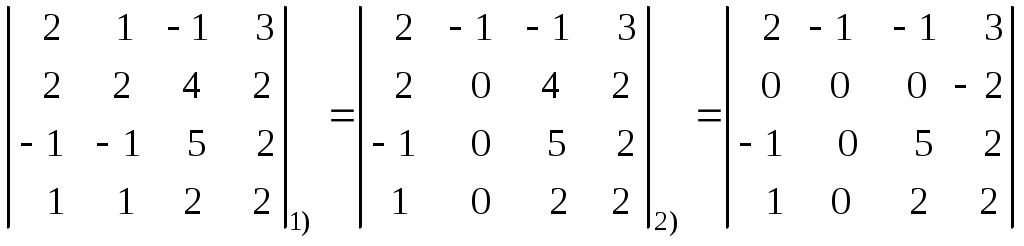 . .Здесь, над определителем последовательно проведены следующие действия: 1) ко 2-му столбцу прибавили 1-й столбец, умноженный на (-1); 2) затем в полученном (втором определителе) ко 2-й строке прибавили 4-ю строку, умноженную на число (-2). В результате этих действий пришли к новому (третьему) определителю, содержащему пять нулевых элементов. Очевиден следующий факт: чем больше нулевых элементов в определителе, тем проще его вычисление. Например, 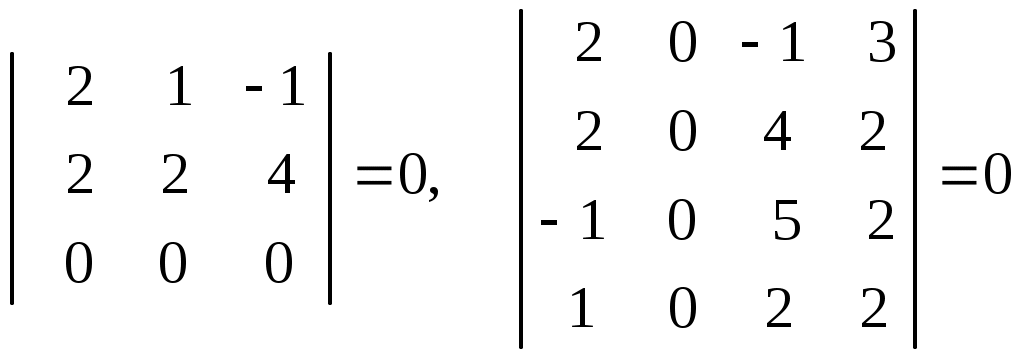 . .Так, например, 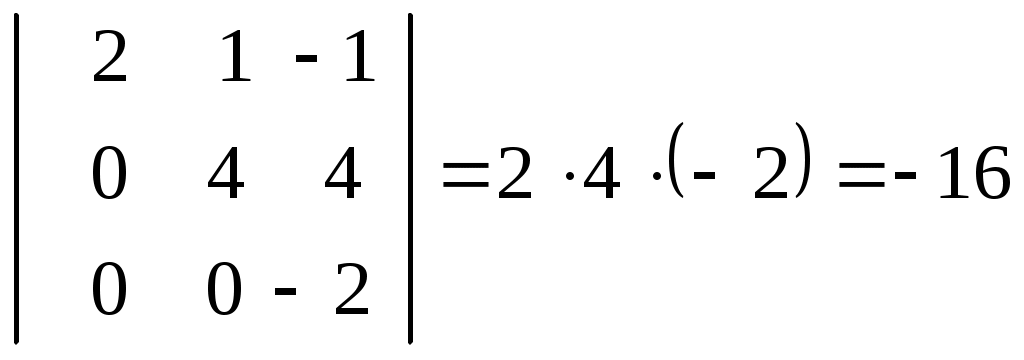 , , 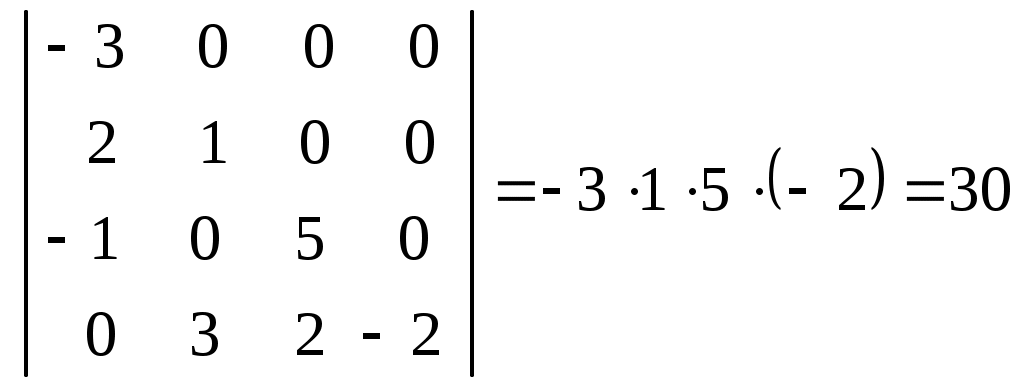 , ,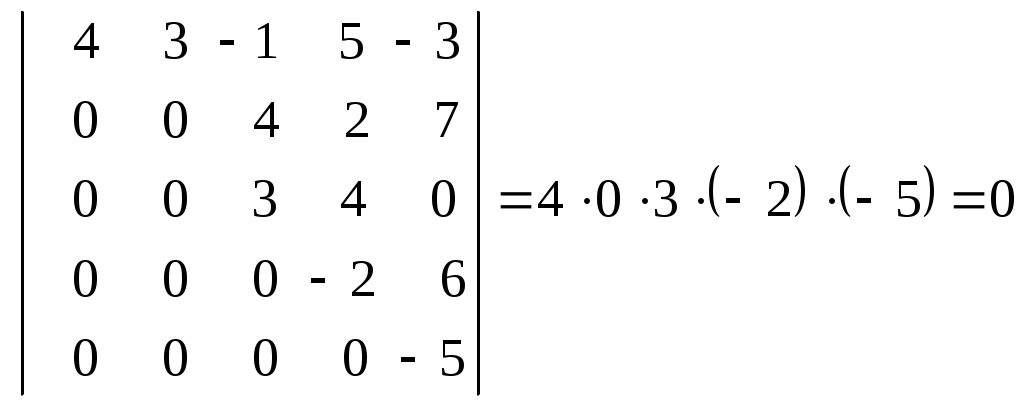 . .Например, 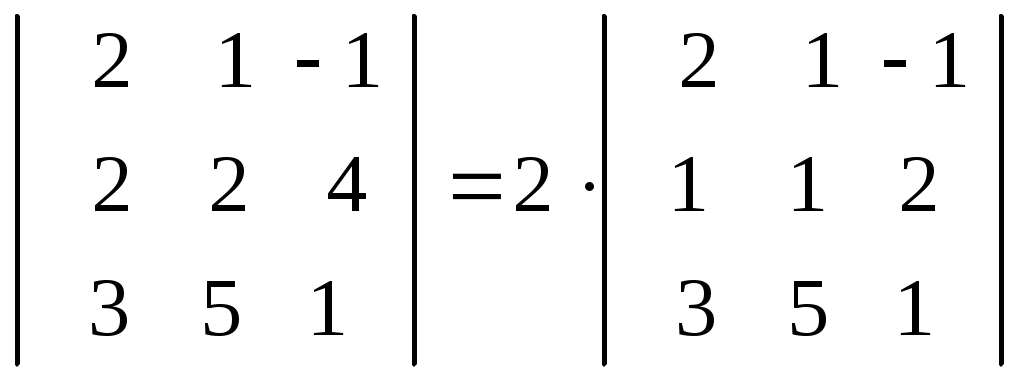 , , 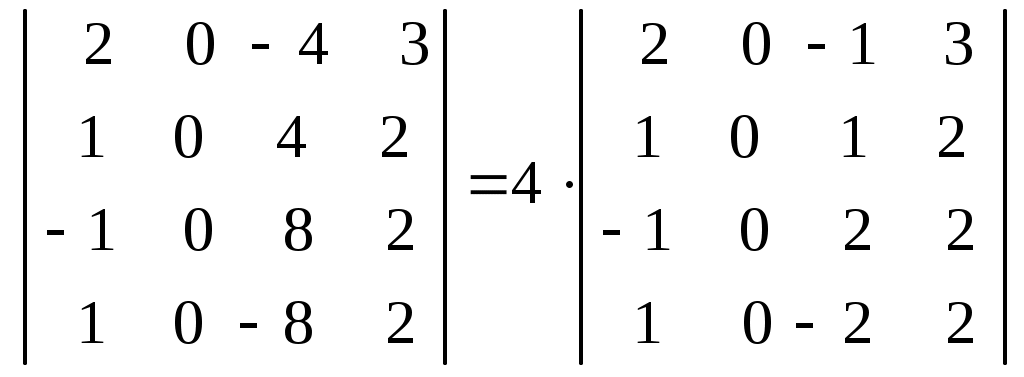 . .В первом определителе множитель 2 вынесен из второй строки. Во втором определителе множитель 4 вынесен из третьего столбца. С помощью свойств Пример 7. Вычислить определитель 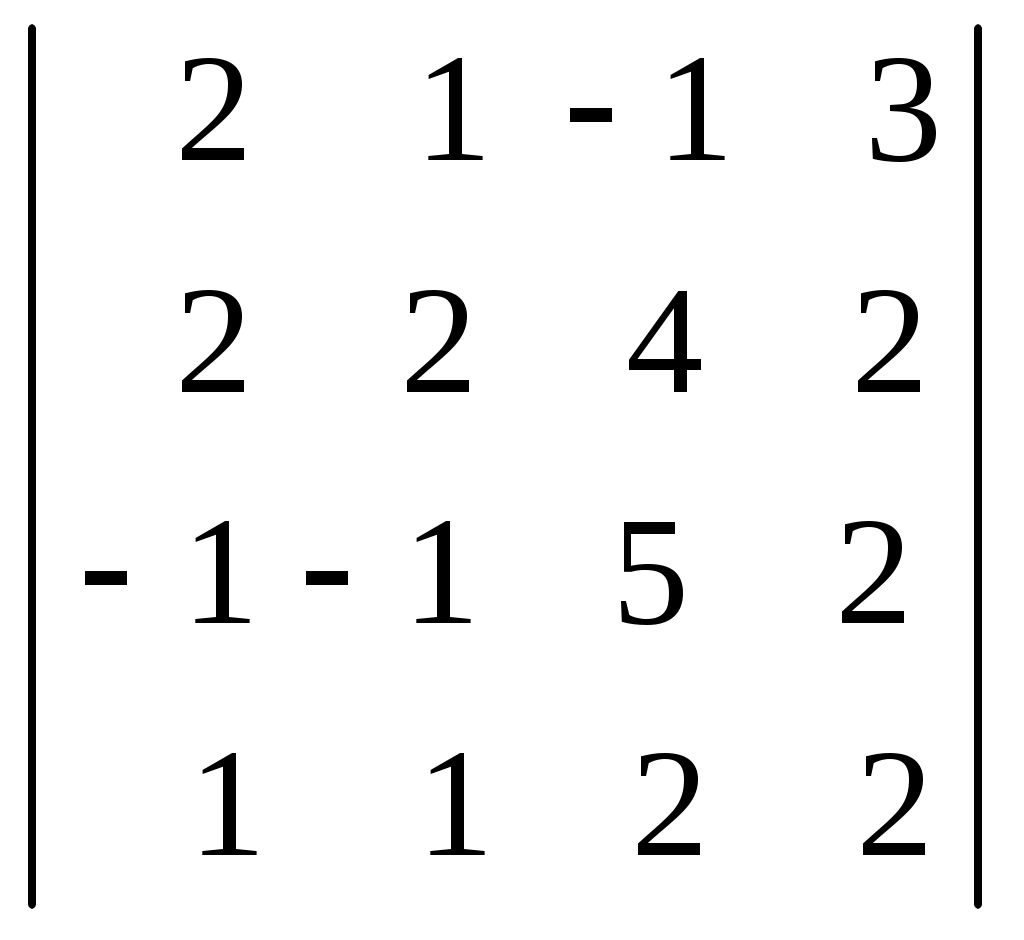 . .Решение. 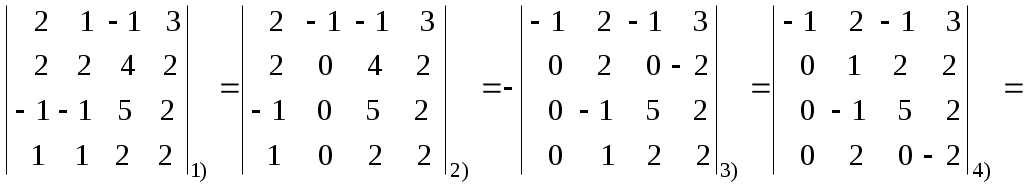 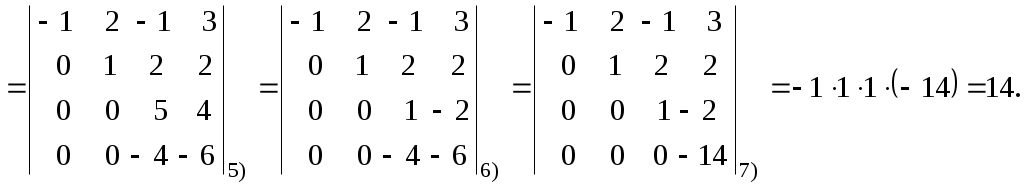 Здесь, при вычислении заданного определителя были последовательно проведены следующие преобразования. 1) В определителе 2) В определителе 3) В определителе 4) В определителе 5) В определителе 6) В определителе 7) Определитель В заключение, отметим следующие факты: 1. Определители матриц 2. Определитель произведения двух квадратных матриц Докажем их для матриц 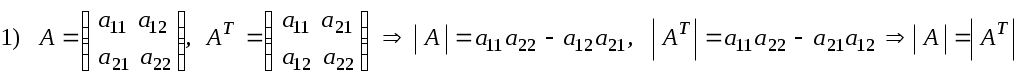 . .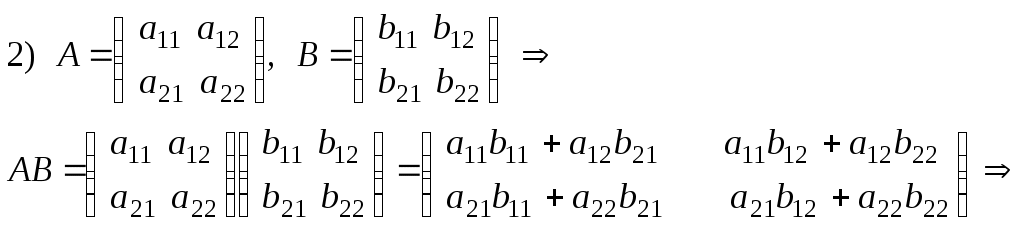 |
