|
|
Лекции по схемотехнике ЭВМ. Лекция Базовые понятия цифровой электроники версия для печати и pda в лекции рассказывается о базовых терминах цифровой электроники, о цифровых сигналах, об уровнях представления цифровых устройств, об их электрических и временных параметрах
Введение в цифровую схемотехнику
|

|

|

|
6. Лекция: Комбинационные микросхемы. Часть 2: версия для печати и PDA
В лекции рассказывается о комбинационных микросхемах: сумматорах, преобразователях кодов, одновибраторах и генераторах, об их алгоритмах работы, параметрах, типовых схемах включения, а также о реализации на их основе некоторых часто встречающихся функций.
|

|

|

| Сумматоры
Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной код - 7 (0111), а второй - 5 (0101), то суммарный код на выходе будет 12 (1100). Сумма двух двоичных чисел с числом разрядов N может иметь число разрядов (N + 1). Например, при суммировании чисел 13 (1101) и 6 (0110) получается число 19 (10011). Поэтому количество выходов сумматора на единицу больше количества разрядов входных кодов. Этот дополнительный (старший) разряд называется выходом переноса.
На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, - ИМ.
Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные числа) и 4-х разрядные (суммируют 4-х разрядные числа). Чаще всего применяют именно 4-разрядные сумматоры. На рис. 6.1 показаны для примера 2-разрядный и 4-разрядный сумматоры. Микросхема ИМ6 отличается от ИМ3 только повышенным быстродействием и номерами используемых выводов микросхемы, функция же выполняется та же самая.
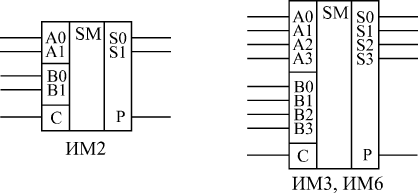
Рис. 6.1. Примеры микросхем сумматоров
Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название - вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.
Для примера в табл. 6.1 приведена полная таблица истинности 2-разрядного сумматора ИМ2. Как видно из таблицы, выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С. Нулевые разряды - младшие, первые разряды - старшие. Полная таблица истинности 4-разрядного сумматора будет чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного сумматора.
Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается, что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.
Таблица 6.1. Таблица истинности микросхемы 2-разрядного сумматора ИМ2
|
Входы
|
Выходы
|
|
C=0
|
C=1
|
A1
|
A0
|
B1
|
B0
|
P
|
S1
|
S0
|
P
|
S1
|
S0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
Рассмотрим пример. Пусть нам надо сложить два числа 5 и 7 в отрицательной логике. Числу 5 в положительной логике соответствует двоичный код 0101, а в отрицательной - код 1010. Числу 7 в положительной логике соответствует двоичный код 0111, а в отрицательной - код 1000. При подаче на вход сумматора кодов 1010 (десятичное число 10 в положительной логике) и 1000 (десятичное число 8 в положительной логике) получаем сумму 10 + 8 = 18, то есть код 10010 в положительной логике. С учетом входного сигнала переноса С=1 (отсутствие входного переноса в отрицательной логике) выходной код сумматора получится на единицу больше: 18 + 1 = 19, то есть 10011. При отрицательной логике это будет соответствовать числу 01100, то есть 12 при отсутствии выходного переноса. В результате получили 5+7=12.
Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал (рис. 6.2).
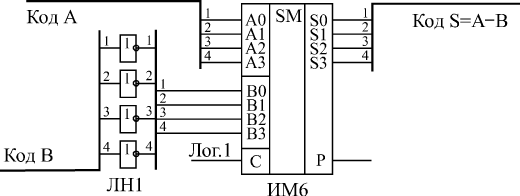
Рис. 6.2. 4-х разрядный вычитатель на сумматоре ИМ6 и инверторах ЛН1
Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.
Еще пример. Пусть надо вычислить разность между числом 12 (1100) и числом 9 (1001). Инвертируем поразрядно 9, получаем 0110, то есть десятичное 6. Находим сумму 12 и 6, получаем 18, а с учетом С = 1 получаем 19, то есть двоичное 10011. В четырех младших разрядах имеем 0011, то есть десятичное 3.
Каскадировать сумматоры для увеличения разрядности очень просто. Надо сигнал с выхода переноса сумматора, обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды (рис. 6.3). При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд (выход переноса Р).
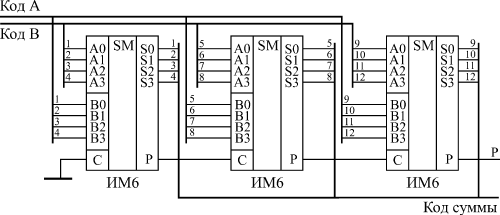
Рис. 6.3. Каскадирование сумматоров ИМ6 для увеличения разрядности
Неопределенные состояния на выходах сумматора могут возникать при любом изменении любого из входных кодов (рис. 6.4). Выходной код суммы может принимать в течение короткого времени значения, никак не связанные с входными кодами, а на выходе переноса могут появляться короткие паразитные импульсы. Это связано прежде всего с неодновременным изменением разрядов входных кодов. Чтобы избежать влияния этих неопределенных состояний на дальнейшую схему, необходимо предусматривать синхронизацию или стробирование выходных сигналов. Но для этого надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.
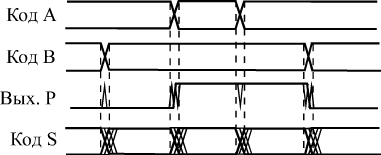
Рис. 6.4. Неопределенные состояния на выходах сумматора при изменении входных кодов
Задержки сумматора ИМ6 от входов до выходов суммы примерно вдвое превышает задержку логического элемента, а от входов до выхода переноса - примерно в полтора раза. Задержки сумматора ИМ3 больше задержек ИМ6 почти вдвое. Поэтому в схемах, где важно быстродействие, лучше использовать ИМ6. Особенно это существенно при каскадировании для увеличения разрядности, так как там задержки отдельных микросхем суммируются. Точные величины задержек надо смотреть в справочниках.
| |
|
|
 Скачать 5.63 Mb.
Скачать 5.63 Mb.



